1.1. Modelos lineales

Los siguientes son un conjunto de métodos destinados a la regresión en el que se espera que el valor objetivo sea una combinación lineal de las características. En notación matemática, si \(\hat{y}\) es el valor predicho.

\[\hat{y}(w, x) = w_0 + w_1 x_1 + ... + w_p x_p\]

En el módulo, designamos el vector \(w = (w_1, ..., w_p)\) como coef_ y \(w_0\) como intercept_.

Para realizar la clasificación con modelos lineales generalizados, ver Regresión logística.

1.1.1. Mínimos Cuadrados Ordinarios

LinearRegression se ajusta a un modelo lineal con coeficientes \(w = (w_1, ... w_p)\) para minimizar la suma residual de cuadrados entre los objetivos observados en el conjunto de datos, y los objetivos predichos por la aproximación lineal. Matemáticamente resuelve un problema de la forma:

\[\min_{w} || X w - y||_2^2\]

LinearRegression tomará en su método fit las matrices X, y y almacenará los coeficientes \(w\) del modelo lineal en su miembro coef_:

>>> from sklearn import linear_model
>>> reg = linear_model.LinearRegression()
>>> reg.fit ([[0, 0], [1, 1], [2, 2]], [0, 1, 2])
LinearRegression()
>>> reg.fit([[0, 0], [1, 1], [2, 2]], [0, 1, 2])
LinearRegression()
>>> reg.coef_
array([0.5, 0.5])

Las estimaciones de los coeficientes de los Mínimos Cuadrados Ordinarios se basan en la independencia de las características. Cuando las características están correlacionadas y las columnas de la matriz de diseño \(X\) tienen una dependencia lineal aproximada, la matriz de diseño se vuelve casi singular y, como resultado, la estimación por mínimos cuadrados se vuelve muy sensible a los errores aleatorios en el objetivo observado, produciendo una gran varianza. Esta situación de multicolinealidad puede surgir, por ejemplo, cuando los datos se recogen sin un diseño experimental.

Ejemplos:

• Ejemplo de regresión lineal

1.1.1.1. Mínimos Cuadrados No-Negativos

Es posible restringir todos los coeficientes para que sean no negativos, lo que puede ser útil cuando representan algunas cantidades físicas o naturalmente no negativas (por ejemplo, conteos de frecuencia o precios de bienes). LinearRegression acepta un parámetro booleano positive: cuando se establece en True se aplican entonces los Mínimos Cuadrados No Negativos.

Ejemplos:

• Mínimos cuadrados no negativos

1.1.1.2. Complejidad de Mínimos Cuadrados Ordinarios

La solución de mínimos cuadrados se calcula utilizando la descomposición del valor singular de X. Si X es una matriz de la forma (n_samples, n_features) este método tiene un costo de \(O(n_{\text{samples}} n_{\text{features}}^2)\), asumiendo que \(n_{\text{samples}} \geq n_{\text{features}}\).

1.1.2. Regresión de cresta y clasificación

1.1.2.1. Regresión

la regresión Ridge aborda algunos de los problemas de Mínimos Cuadrados Ordinarios imponiendo una sanción al tamaño de los coeficientes. Los coeficientes de rudimentos minimizan una suma residual penalizada de cuadrados:

\[\min_{w} || X w - y||_2^2 + \alpha ||w||_2^2\]

El parámetro de complejidad \(\alpha \geq 0\) controla la cantidad de contracción: cuanto mayor sea el valor de \(\alpha\), mayor será la cantidad de contracción y, por tanto, los coeficientes serán más robustos a la colinealidad.

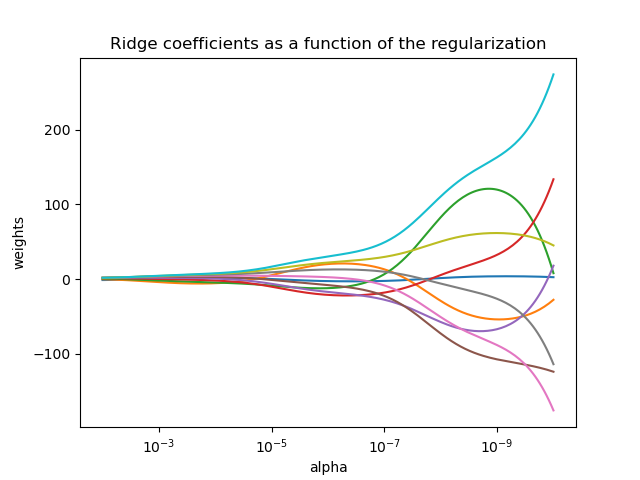
Al igual que con otros modelos lineales, Ridge tomará en su método fit las matrices X, y y almacenará los coeficientes \(w\) del modelo lineal en su miembro coef_:

>>> from sklearn import linear_model
>>> reg = linear_model.Ridge(alpha=.5)
>>> reg.fit([[0, 0], [0, 0], [1, 1]], [0, .1, 1])
Ridge(alpha=0.5)
>>> reg.coef_
array([0.34545455, 0.34545455])
>>> reg.intercept_
0.13636...

1.1.2.2. Clasificación

El regresor Ridge tiene una variante de clasificador: RidgeClassifier. Este clasificador primero convierte los objetivos binarios a {-1, 1} y luego trata el problema como una tarea de regresión, optimizando el mismo objetivo que el anterior. La clase predicha corresponde al signo de la predicción del regresor. Para la clasificación multiclase, el problema se trata como una regresión de salida múltiple, y la clase predicha corresponde a la salida con el valor más alto.

Podría parecer cuestionable utilizar una pérdida de mínimos cuadrados (penalizada) para ajustar un modelo de clasificación en lugar de las pérdidas logísticas o de bisagra más tradicionales. Sin embargo, en la práctica todos esos modelos pueden conducir a puntuaciones de validación cruzada similares en términos de exactitud o precisión/recuperación, mientras que la pérdida de mínimos cuadrados penalizada utilizada por el RidgeClassifier permite una elección muy diferente de los solucionadores numéricos con distintos perfiles de rendimiento computacional.

El RidgeClassifier puede ser significativamente más rápido que, por ejemplo, LogisticRegression con un elevado número de clases, porque es capaz de calcular la matriz de proyección \((X^T X)^{-1} X^T\) sólo una vez.

Este clasificador se denomina a veces Máquinas de vectores de soporte de mínimos cuadrados con un núcleo lineal.

Ejemplos:

• Graficar los coeficientes de Ridge en función de la regularización

• Clasificación de documentos de texto utilizando características dispersas

• Errores comunes en la interpretación de los coeficientes de los modelos lineales

1.1.2.3. Complejidad cresta

Este método tiene el mismo orden de complejidad que Mínimos Cuadrados Ordinarios.

1.1.2.4. Ajuste del parámetro de regularización: Validación cruzada con exclusión (leave-one-out)

RidgeCV implementa la regresión de cresta con validación cruzada incorporada del parámetro alfa. El objeto funciona de la misma manera que GridSearchCV, excepto que por defecto utiliza la validación cruzada con exclusión:

>>> import numpy as np
>>> from sklearn import linear_model
>>> reg = linear_model.RidgeCV(alphas=np.logspace(-6, 6, 13))
>>> reg.fit([[0, 0], [0, 0], [1, 1]], [0, .1, 1])
RidgeCV(alphas=array([1.e-06, 1.e-05, 1.e-04, 1.e-03, 1.e-02, 1.e-01, 1.e+00, 1.e+01,
      1.e+02, 1.e+03, 1.e+04, 1.e+05, 1.e+06]))
>>> reg.alpha_
0.01

Si se especifica el valor del atributo cv se activará el uso de la validación cruzada con GridSearchCV, por ejemplo cv=10 para la validación cruzada de 10 veces, en lugar de la validación cruzada Leave-One-Out.

Referencias

• «Notes on Regularized Least Squares», Rifkin & Lippert (reporte técnico, láminas del curso).

1.1.3. Lasso

El Lasso es un modelo lineal que estima coeficientes dispersos. Es útil en algunos contextos debido a su tendencia a preferir soluciones con menos coeficientes distintos de cero, reduciendo efectivamente el número de características de las que depende la solución dada. Por esta razón, Lasso y sus variantes son fundamentales en el campo de la detección comprimida. Bajo ciertas condiciones, puede recuperar el conjunto exacto de coeficientes no nulos (ver Detección compresiva: reconstrucción de la tomografía con a priori L1 (Lasso)).

Matemáticamente, consiste en un modelo lineal con un término de regularización añadido. La función objetivo a minimizar es:

\[\min_{w} { \frac{1}{2n_{\text{samples}}} ||X w - y||_2 ^ 2 + \alpha ||w||_1}\]

La estimación lasso resuelve así la minimización de la penalización por mínimos cuadrados con \(\alpha ||w|_1\) añadido, donde \(\alpha\) es una constante y \(|w||_1\) es la norma \(\ell_1\) del vector de coeficientes.

La implementación en la clase Lasso utiliza el descenso por coordenadas como algoritmo para ajustar los coeficientes. Ver Regresión de ángulo mínimo para otra implementación:

>>> from sklearn import linear_model
>>> reg = linear_model.Lasso(alpha=0.1)
>>> reg.fit([[0, 0], [1, 1]], [0, 1])
Lasso(alpha=0.1)
>>> reg.predict([[1, 1]])
array([0.8])

La función lasso_path es útil para tareas de nivel inferior, ya que calcula los coeficientes a lo largo de todo el recorrido de valores posibles.

Ejemplos:

• Lasso y red elástica para señales dispersas

• Detección compresiva: reconstrucción de la tomografía con a priori L1 (Lasso)

• Errores comunes en la interpretación de los coeficientes de los modelos lineales

Nota

Selección de características con Lasso

Como la regresión Lasso produce modelos dispersos, puede utilizarse para realizar la selección de características, como se detalla en Selección de características basada en L1.

Las siguientes dos referencias explican las iteraciones utilizadas en el solucionador de descenso de coordenadas de scikit-learn, así como el cálculo de la brecha de dualidad utilizado para el control de la convergencia.

Referencias

• «Regularization Path For Generalized linear Models by Coordinate Descent», Friedman, Hastie & Tibshirani, J Stat Softw, 2010 (Paper).

• «An Interior-Point Method for Large-Scale L1-Regularized Least Squares,» S. J. Kim, K. Koh, M. Lustig, S. Boyd and D. Gorinevsky, en IEEE Journal of Selected Topics in Signal Processing, 2007 (Paper)

1.1.3.1. Ajuste del parámetro de regularización

El parámetro alpha controla el grado de dispersión de los coeficientes estimados.

1.1.3.1.1. Utilizando validación cruzada

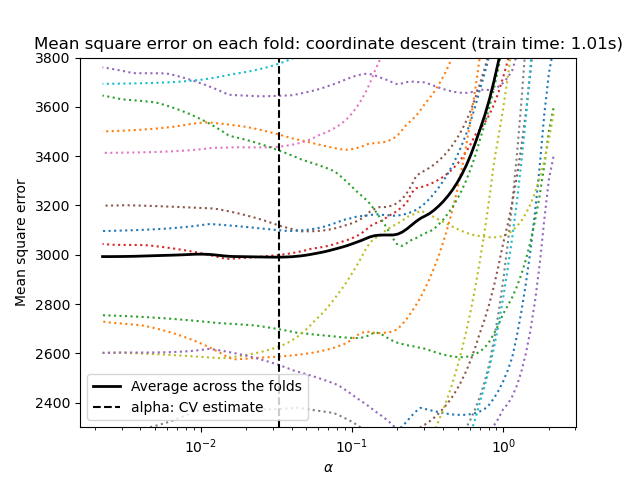
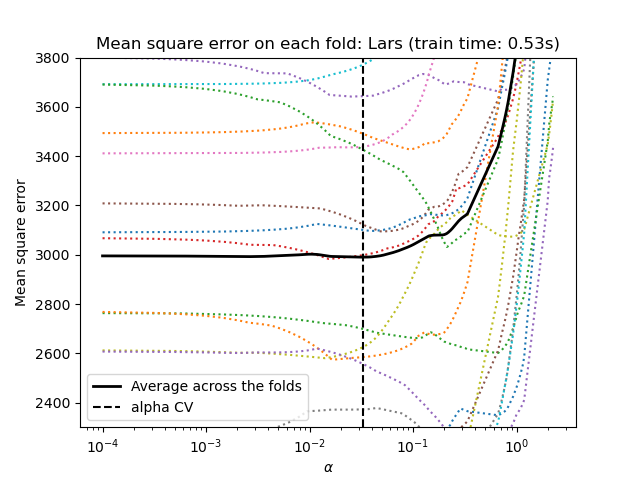
scikit-learn expone objetos que establecen el parámetro alpha de Lasso por validación cruzada: LassoCV y LassoLarsCV. LassoLarsCV se basa en el algoritmo Regresión de ángulo mínimo que se explica a continuación.

Para conjuntos de datos de alta dimensión con muchas características colineales, LassoCV suele ser preferible. Sin embargo, LassoLarsCV tiene la ventaja de explorar valores más relevantes del parámetro alpha, y si el número de muestras es muy pequeño comparado con el número de características, suele ser más rápido que LassoCV.

1.1.3.1.2. Selección de modelos basada en criterios de información

Como alternativa, el estimador LassoLarsIC propone utilizar el criterio de información de Akaike (AIC) y el criterio de información de Bayes (BIC). Se trata de una alternativa computacionalmente más barata para encontrar el valor óptimo de alfa, ya que el camino de regularización se calcula sólo una vez en lugar de k+1 veces cuando se utiliza la validación cruzada k-fold. Sin embargo, estos criterios necesitan una estimación adecuada de los grados de libertad de la solución, se derivan para muestras grandes (resultados asintóticos) y suponen que el modelo es correcto, es decir, que los datos son realmente generados por este modelo. También tienden a fallar cuando el problema está mal condicionado (más características que muestras).

Ejemplos:

• Selección del modelo Lasso: Validación cruzada / AIC / BIC

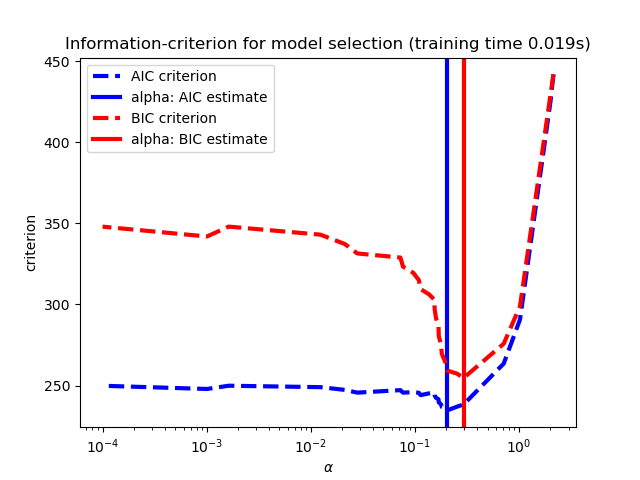
1.1.3.1.3. Comparación con el parámetro de regularización de SVM

La equivalencia entre alpha y el parámetro de regularización de SVM, C viene dada por alpha = 1 / C o alpha = 1 / (n/samples * C), dependiendo del estimador y de la función objetivo exacta optimizada por el modelo.

1.1.4. Lasso multitarea

La MultiTaskLasso es un modelo lineal que estima coeficientes dispersos para problemas de regresión múltiple de forma conjunta: y es un arreglo 2D, de forma (n_samples, n_tasks). La restricción es que las características seleccionadas son las mismas para todos los problemas de regresión, también llamados tareas.

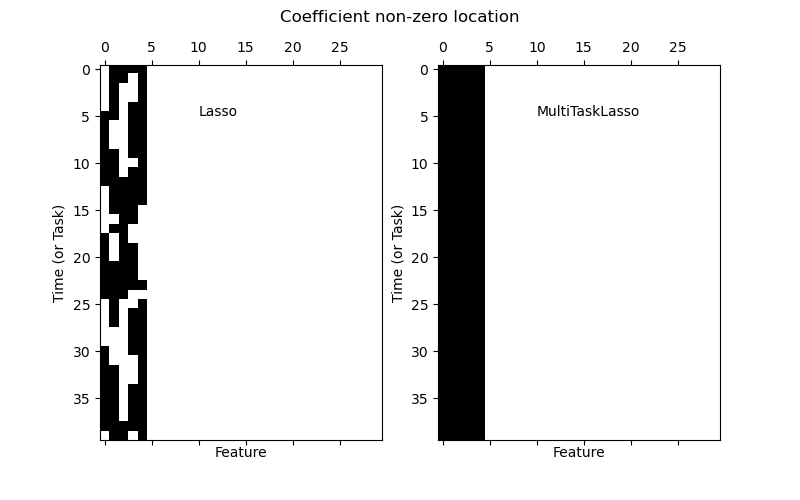
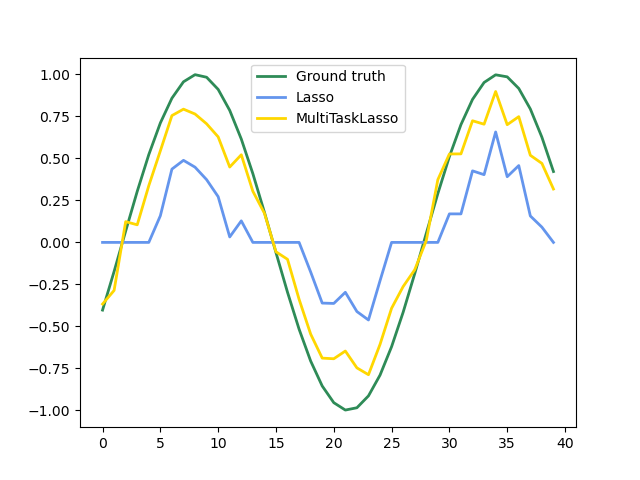
La siguiente figura compara la ubicación de las entradas no nulas en la matriz de coeficientes W obtenida con un Lasso simple o un MultiTaskLasso. Las estimaciones de Lasso producen no ceros dispersos mientras que los no ceros del MultiTaskLasso son columnas completas.

Ajustar un modelo de serie de tiempo, imponiendo que cualquier característica activa esté presente en todo momento.

Ejemplos:

• Selección conjunta de características con Lasso multitarea

Matemáticamente, consiste en un modelo lineal entrenado con una norma mixta \(\ell_1\) \(\ell_2\) para la regularización. La función objetivo a minimizar es:

\[\min_{W} { \frac{1}{2n_{\text{samples}}} ||X W - Y||_{\text{Fro}} ^ 2 + \alpha ||W||_{21}}\]

donde \(\text{Fro}\) indica la norma de Frobenius

\[||A||_{\text{Fro}} = \sqrt{\sum_{ij} a_{ij}^2}\]

y \(\ell_1\) \(\ell_2\) se lee

\[||A||_{2 1} = \sum_i \sqrt{\sum_j a_{ij}^2}.\]

La implementación en la clase MultiTaskLasso utiliza el descenso de coordenadas como algoritmo para ajustar los coeficientes.

1.1.5. Elastic-Net

La clase ElasticNet es un modelo de regresión lineal entrenado con la regularización de los coeficientes mediante las normas \(\ell_1\) y \(\ell_2\). Esta combinación permite aprender un modelo disperso en el que pocos pesos son distintos de cero, como en Lasso, pero manteniendo las propiedades de regularización de Ridge. Controlamos la combinación convexa de \(\ell_1\) y \(\ell_2\) utilizando el parámetro l1_ratio.

Elastic-net es útil cuando hay múltiples características que están correlacionadas entre sí. Lasso es probable que elija una de ellas al azar, mientras que elastic-net es probable que elija ambas.

Una ventaja práctica del intercambio entre Lasso y Cresta es que permite que Elastic-Net herede parte de la estabilidad de Cresta bajo la rotación.

La función objetivo a minimizar es en este caso

\[\min_{w} { \frac{1}{2n_{\text{samples}}} ||X w - y||_2 ^ 2 + \alpha \rho ||w||_1 + \frac{\alpha(1-\rho)}{2} ||w||_2 ^ 2}\]

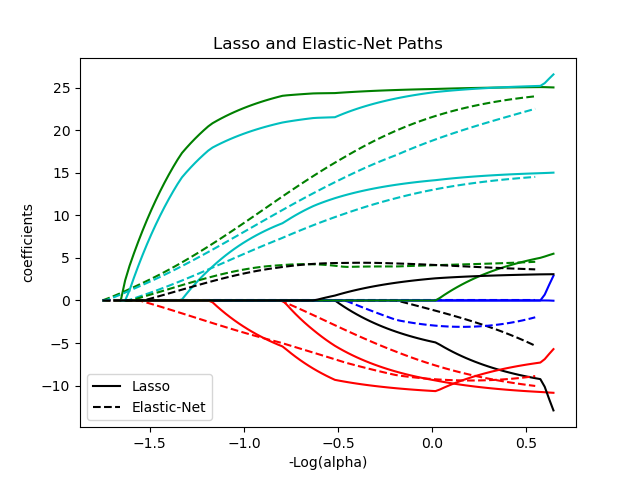
La clase ElasticNetCV puede utilizarse para establecer los parámetros alpha (\(\alpha\)) y l1_ratio (\(\rho\)) mediante validación cruzada.

Ejemplos:

• Lasso y red elástica para señales dispersas

• Lasso y red elástica

Las siguientes dos referencias explican las iteraciones utilizadas en el solucionador de descenso de coordenadas de scikit-learn, así como el cálculo de la brecha de dualidad utilizado para el control de la convergencia.

Referencias

• «Regularization Path For Generalized linear Models by Coordinate Descent», Friedman, Hastie & Tibshirani, J Stat Softw, 2010 (Paper).

• «An Interior-Point Method for Large-Scale L1-Regularized Least Squares,» S. J. Kim, K. Koh, M. Lustig, S. Boyd and D. Gorinevsky, en IEEE Journal of Selected Topics in Signal Processing, 2007 (Paper)

1.1.6. Elastic-Net multitarea

El MultiTaskElasticNet es un modelo de red elástica que estima coeficientes dispersos para problemas de regresión múltiple de forma conjunta: Y es una arreglo 2D de forma (n_samples, n_tasks). La restricción es que las características seleccionadas son las mismas para todos los problemas de regresión, también llamados tareas.

Matemáticamente, consiste en un modelo lineal entrenado con una norma mixta \(\ell_1\) \(\ell_2 y una norma :math:\)ell_2` para la regularización. La función objetivo a minimizar es:

\[\min_{W} { \frac{1}{2n_{\text{samples}}} ||X W - Y||_{\text{Fro}}^2 + \alpha \rho ||W||_{2 1} + \frac{\alpha(1-\rho)}{2} ||W||_{\text{Fro}}^2}\]

La implementación en la clase MultiTaskElasticNet utiliza el descenso por coordenadas como algoritmo para ajustar los coeficientes.

La clase MultiTaskElasticNetCV puede utilizarse para establecer los parámetros alpha (\(\alpha\)) y l1_ratio (\(\rho\)) mediante validación cruzada.

1.1.7. Regresión de ángulo mínimo

La regresión de ángulo mínimo (LARS) es un algoritmo de regresión para datos de alta dimensión, desarrollado por Bradley Efron, Trevor Hastie, Iain Johnstone y Robert Tibshirani. LARS es similar a la regresión escalonada. En cada paso, encuentra la característica más correlacionada con el objetivo. Cuando hay varias características que tienen la misma correlación, en lugar de continuar a lo largo de la misma característica, procede en una dirección equiangular entre las características.

Las ventajas de LARS son:

• Es numéricamente eficiente en contextos donde el número de características es significativamente mayor que el número de muestras.

• Es computacionalmente tan rápido como la selección directa y tiene el mismo orden de complejidad que los mínimos cuadrados ordinarios.

• Produce una ruta de solución lineal completa a trozos, que es útil en la validación cruzada o en intentos similares de ajustar el modelo.

• Si dos características están casi igualmente correlacionadas con el objetivo, sus coeficientes deberían aumentar aproximadamente al mismo ritmo. Así, el algoritmo se comporta como la intuición espera, y además es más estable.

• Se puede modificar fácilmente para producir soluciones para otros estimadores, como el Lasso.

Las desventajas del método LARS son:

• Dado que el LARS se basa en un reajuste iterativo de los residuos, parece ser especialmente sensible a los efectos del ruido. Este problema es discutido en detalle por Weisberg en la sección de discusión del artículo de Efron et al. (2004) Annals of Statistics.

El modelo LARS puede emplearse utilizando el estimador Lars, o su implementación de bajo nivel lars_path o lars_path_gram.

1.1.8. LARS Lasso

LassoLars es un modelo lasso implementado mediante el algoritmo LARS, y a diferencia de la implementación basada en el descenso de coordenadas, éste proporciona la solución exacta, que es lineal a trozos en función de la norma de sus coeficientes.

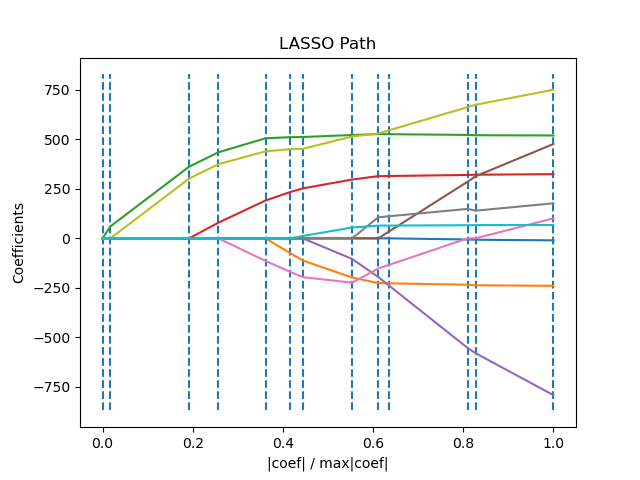
>>> from sklearn import linear_model
>>> reg = linear_model.LassoLars(alpha=.1)
>>> reg.fit([[0, 0], [1, 1]], [0, 1])
LassoLars(alpha=0.1)
>>> reg.coef_
array([0.717157..., 0.        ])

Ejemplos:

• Trayectoria de Lasso utilizando LARS

El algoritmo Lars proporciona la trayectoria completa de los coeficientes a lo largo del parámetro de regularización casi sin esfuerzo, por lo que una operación común es recuperar la trayectoria con una de las funciones lars_path o lars_path_gram.

1.1.8.1. Formulación matemática

El algoritmo es similar al de la regresión escalonada hacia adelante, pero en lugar de incluir características en cada paso, los coeficientes estimados se incrementan en una dirección equiangular a las correlaciones de cada uno con el residuo.

En lugar de dar un resultado vectorial, la solución LARS consiste en una curva que denota la solución para cada valor de la norma \(\ell_1\) del vector de parámetros. La ruta completa de los coeficientes se almacena en la matriz coef_path_, que tiene un tamaño (n_features, max_features+1). La primera columna es siempre cero.

Referencias:

• El algoritmo original se detalla en el artículo Least Angle Regression de Hastie et al.

1.1.9. Búsqueda de coincidencias ortogonales (OMP)

OrthogonalMatchingPursuit y orthogonal_mp implementan el algoritmo OMP para aproximar el ajuste de un modelo lineal con restricciones impuestas en el número de coeficientes no nulos (es decir, la pseudo-norma \(\ell_0\)).

Al ser un método de selección de características hacia adelante, como Regresión de ángulo mínimo, la búsqueda de coincidencias ortogonales puede aproximar el vector de solución óptima con un número fijo de elementos distintos de cero:

\[\underset{w}{\operatorname{arg\,min\,}} ||y - Xw||_2^2 \text{ subject to } ||w||_0 \leq n_{\text{nonzero\_coefs}}\]

Alternativamente, la búsqueda ortogonal de coincidencias puede tener como objetivo un error específico en lugar de un número específico de coeficientes distintos de cero. Esto puede expresarse como:

\[\underset{w}{\operatorname{arg\,min\,}} ||w||_0 \text{ subject to } ||y-Xw||_2^2 \leq \text{tol}\]

OMP se basa en un algoritmo ambicioso que incluye en cada paso el átomo más correlacionado con el residuo actual. Es similar al método más sencillo de búsqueda de coincidencias (MP), pero mejor en el sentido de que, en cada iteración, el residuo se vuelve a calcular utilizando una proyección ortogonal sobre el espacio de los elementos del diccionario elegido previamente.

Ejemplos:

• Búsqueda de correspondencias ortogonales

Referencias:

• https://www.cs.technion.ac.il/~ronrubin/Publications/KSVD-OMP-v2.pdf

• Matching pursuits with time-frequency dictionaries, S. G. Mallat, Z. Zhang,

1.1.10. Regresión bayesiana

Las técnicas de regresión bayesiana pueden utilizarse para incluir parámetros de regularización en el procedimiento de estimación: el parámetro de regularización no se establece en un sentido estricto, sino que se ajusta a los datos disponibles.

Esto se puede hacer introduciendo distribuciones a priori no informativas sobre los hiperparámetros del modelo. La regularización \(\ell_{2}\) utilizada en Regresión de cresta y clasificación es equivalente a encontrar una estimación máxima a posteriori bajo una distribución a priori gaussiana sobre los coeficientes \(w\) con precisión \(\lambda^{-1}\). En lugar de establecer manualmente lambda, es posible tratarla como una variable aleatoria que debe estimarse a partir de los datos.

Para obtener un modelo totalmente probabilístico, se supone que la salida \(y\) se distribuye de forma gaussiana alrededor de \(X w\):

\[p(y|X,w,\alpha) = \mathcal{N}(y|X w,\alpha)\]

donde \(\alpha\) se trata de nuevo como una variable aleatoria que debe estimarse a partir de los datos.

Las ventajas de la regresión bayesiana son:

• Se adapta a los datos en cuestión.

• Puede utilizarse para incluir parámetros de regularización en el procedimiento de estimación.

Las desventajas de la regresión bayesiana son:

• La inferencia del modelo puede llevar mucho tiempo.

Referencias

• Una buena introducción a los métodos bayesianos se encuentra en C. Bishop: Pattern Recognition and Machine learning

• El algoritmo original se detalla en el libro Bayesian learning for neural networks by Radford M. Neal

1.1.10.1. Regresión Bayesiana de Cresta

BayesianRidge estima un modelo probabilístico del problema de regresión como se ha descrito anteriormente. La distribución a priori para el coeficiente \(w\) viene dada por una gaussiana esférica:

\[p(w|\lambda) = \mathcal{N}(w|0,\lambda^{-1}\mathbf{I}_{p})\]

Las distribuciones a priori sobre \(\alpha\) y \(lambda\) se eligen para ser distribuciones gamma, la conjugada a priori para la precisión de la distribución gaussiana. El modelo resultante se llama Regresión Bayesiana de Cresta, y es similar al clásico Ridge.

Los parámetros \(w\), \(\alpha\) y \(lambda\) se estiman conjuntamente durante el ajuste del modelo, los parámetros de regularización \(\alpha\) y \(lambda\) se estiman maximizando la verosimilitud marginal log. La implementación de scikit-learn se basa en el algoritmo descrito en el Apéndice A de (Tipping, 2001) donde la actualización de los parámetros \(\alpha\) y \(lambda\) se realiza como se sugiere en (MacKay, 1992). El valor inicial del procedimiento de maximización se puede establecer con los hiperparámetros alpha_init y lambda_init.

Hay cuatro hiperparámetros más, \(\alpha_1\), \(\alpha_2\), \(lambda_1\) y \(lambda_2\) de las distribuciones previas gamma sobre \(\alpha\) y \(lambda\). Normalmente se eligen para que sean no informativas. Por defecto \(\alpha_1 = \alpha_2 = \lambda_1 = \lambda_2 = 10^{-6}\).

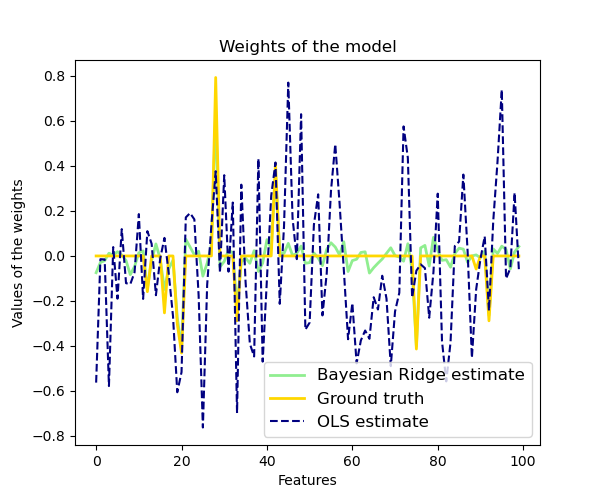
La regresión Bayesiana de Cresta se utiliza para la regresión:

>>> from sklearn import linear_model
>>> X = [[0., 0.], [1., 1.], [2., 2.], [3., 3.]]
>>> Y = [0., 1., 2., 3.]
>>> reg = linear_model.BayesianRidge()
>>> reg.fit(X, Y)
BayesianRidge()

Después de ser ajustado, el modelo puede ser utilizado para predecir nuevos valores:

>>> reg.predict([[1, 0.]])
array([0.50000013])

Se puede acceder a los coeficientes \(w\) del modelo:

>>> reg.coef_
array([0.49999993, 0.49999993])

Debido al framework bayesiano, los pesos encontrados son ligeramente diferentes a los encontrados por Mínimos Cuadrados Ordinarios. Sin embargo, la regresión Bayesiana de Cresta es más robusta frente a los problemas mal definidos.

Ejemplos:

• Regresión Bayesiana de Cresta

• Ajuste de curvas con regresión Bayesiana Ridge

Referencias:

• Sección 3.3 en Christopher M. Bishop: Pattern Recognition and Machine Learning, 2006

• David J. C. MacKay, Bayesian Interpolation, 1992.

• Michael E. Tipping, Sparse Bayesian Learning and the Relevance Vector Machine, 2001.

1.1.10.2. Determinación automática de la relevancia - ARD

ARDRegression es muy similar a la Regresión Bayesiana de Cresta, pero puede dar lugar a coeficientes \(w\) más dispersos 1 2. ARDRegression plantea una distribución a priori diferente sobre \(w\), al abandonar la suposición de que la gaussiana es esférica.

En su lugar, se asume que la distribución sobre \(w\) es una distribución Gaussiana elíptica paralela al eje.

Esto significa que cada coeficiente \(w_{i}\) se extrae de una distribución Gaussiana, centrada en cero y con una precisión \(\lambda_{i}\):

\[p(w|\lambda) = \mathcal{N}(w|0,A^{-1})\]

with \(\text{diag}(A) = \lambda = \{\lambda_{1},...,\lambda_{p}\}\).

En contraste con la Regresión Bayesiana de Cresta, cada coordenada de \(w_{i}\) tiene su propia desviación estándar \(lambda_i\). La distribución a priori sobre todos los \(lambda_i\) se elige para ser la misma distribución gamma dada por los hiperparámetros \(lambda_1\) y \(lambda_2\).

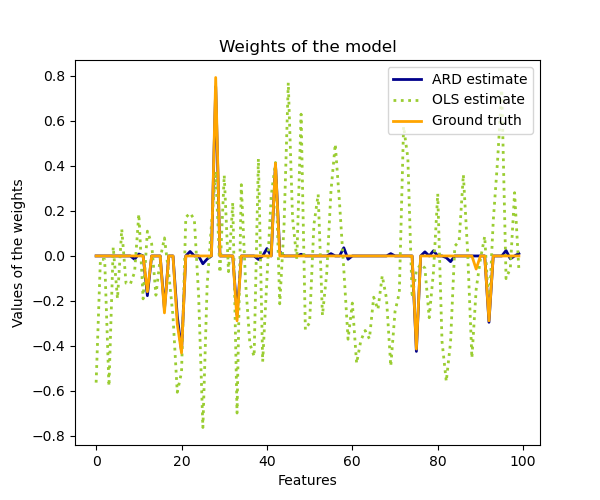
El ARD también se conoce en la literatura como Aprendizaje Bayesiano Disperso y Máquina de Vectores de Relevancia 3 4.

Ejemplos:

• Regresión automática de determinación de la relevancia (ARD)

Referencias:

1

Christopher M. Bishop: Pattern Recognition and Machine Learning, Capítulo 7.2.1

2

David Wipf and Srikantan Nagarajan: A new view of automatic relevance determination

3

Michael E. Tipping: Sparse Bayesian Learning and the Relevance Vector Machine

4

Tristan Fletcher: Relevance Vector Machines explained

1.1.11. Regresión logística

La regresión logística, a pesar de su nombre, es un modelo lineal de clasificación más que de regresión. La regresión logística también se conoce en la literatura como regresión logit, clasificación de máxima entropía (MaxEnt) o clasificador log-lineal. En este modelo, las probabilidades que describen los posibles resultados de un único ensayo se modelan mediante una función logística.

La regresión logística se implementa en LogisticRegression. Esta implementación puede ajustar la regresión logística binaria, One-vs-Rest o multinomial con regularización opcional \(\ell_1\), \(\ell_2\) o Elastic-Net.

Nota

La regularización se aplica por defecto, lo que es habitual en el aprendizaje automático pero no en la estadística. Otra ventaja de la regularización es que mejora la estabilidad numérica. La ausencia de regularización equivale a fijar C en un valor muy alto.

Como problema de optimización, la regresión logística penalizada de clase binaria \(\ell_2\) minimiza la siguiente función de coste:

\[\min_{w, c} \frac{1}{2}w^T w + C \sum_{i=1}^n \log(\exp(- y_i (X_i^T w + c)) + 1) .\]

Del mismo modo, la regresión logística regularizada \(\ell_1\) resuelve el siguiente problema de optimización:

\[\min_{w, c} \|w\|_1 + C \sum_{i=1}^n \log(\exp(- y_i (X_i^T w + c)) + 1).\]

La regularización Elastic-Net es una combinación de \(\ell_1\) y \(\ell_2\), y minimiza la siguiente función de costo:

\[\min_{w, c} \frac{1 - \rho}{2}w^T w + \rho \|w\|_1 + C \sum_{i=1}^n \log(\exp(- y_i (X_i^T w + c)) + 1),\]

donde \(\rho\) controla la fuerza de la regularización \(\ell_1\) frente a la regularización \(\ell_2\) (corresponde al parámetro l1_ratio).

Ten en cuenta que, en esta notación, se supone que el objetivo \(y_i\) toma valores en el conjunto \({-1, 1}\) en el ensayo \(i\). También podemos ver que Elastic-Net es equivalente a \(\ell_1\) cuando \(\rho = 1\) y equivalente a \(\ell_2\) cuando \(\rho=0\).

Los solucionadores implementados en la clase LogisticRegression son «liblinear», «newton-cg», «lbfgs», «sag» y «saga»:

El solucionador «liblinear» utiliza un algoritmo de descenso de coordenadas (CD), y se basa en la excelente biblioteca C++ LIBLINEAR, que se entrega con scikit-learn. Sin embargo, el algoritmo CD implementado en liblinear no puede aprender un verdadero modelo multinomial (multiclase); en su lugar, el problema de optimización se descompone de una manera «uno-vs-resto» para que se entrenen clasificadores binarios separados para todas las clases. Esto sucede lejos de la vista del usuario, así que las instancias de LogisticRegression que utilizan este solucionador se comportan como clasificadores multiclase. Para la regularización \(\ell_1\) sklearn.svm.l1_min_c permite calcular el límite inferior de C para obtener un modelo no «nulo» (todos los pesos de las características a cero).

Los solucionadores «lbfgs», «sag» y «newton-cg» sólo admiten la regularización \(\ell_2\) o ninguna regularización, y se considera que convergen más rápidamente para algunos datos de alta dimensión. Al establecer multi_class a «multinomial» con estos solucionadores se aprende un verdadero modelo de regresión logística multinomial 5, lo que significa que sus estimaciones de probabilidad deberían estar mejor calibradas que la configuración predeterminada «one-vs-rest».

El solucionador «sag» utiliza el descenso de gradiente promedio estocástico 6. Es más rápido que otros solucionadores para grandes conjuntos de datos, cuando tanto el número de muestras como el número de características son grandes.

El solucionador «saga» 7 es una variante de «sag» que también admite la opción no suave penalty="l1". Por lo tanto, este es el solucionador de elección para la regresión logística multinomial dispersa. También es el único solucionador que admite penalty="elasticnet".

El «lbfgs» es un algoritmo de optimización que se aproxima al algoritmo Broyden-Fletcher-Goldfarb-Shanno 8, que pertenece a los métodos quasi-Newton. El solucionador «lbfgs» se recomienda para conjuntos de datos pequeños, pero para conjuntos de datos más grandes su rendimiento se reduce. 9

La siguiente tabla resume las penalizaciones que admite cada solucionador:

	Solucionadores
Penalizaciones	“liblinear”	“lbfgs”	“newton-cg”	“sag”	“saga”
Multinomial + penalización L2	no	si	si	si	si
OVR + penalización L2	si	si	si	si	si
Multinomial + penalización L1	no	no	no	no	si
OVR + penalización L1	si	no	no	no	si
Elastic-Net	no	no	no	no	si
Ninguna penalización (“none”)	no	si	si	si	si
Comportamientos
Penalizar el intercepto (malo)	si	no	no	no	no
Más rápido para conjuntos de datos grandes	no	no	no	si	si
Robusto para conjuntos de datos no escalados	si	si	si	no	no

El solucionador «lbfgs» se utiliza por defecto por su robustez. Para conjuntos de datos grandes, el solucionador «saga» suele ser más rápido. Para conjuntos de datos grandes, también se puede considerar el uso de SGDClassifier con pérdida “log”, que puede ser incluso más rápido pero requiere más ajustes.

Ejemplos:

• Penalización L1 y dispersión en la regresión logística

• Ruta de regularización de la regresión logística L1

• Trazar la regresión logística multinomial y de One-vs-Rest

• Regresión logística dispersa multiclase en 20 nuevos grupos

• Clasificación MNIST mediante logística multinomial + L1

Diferencias con liblinear:

Puede haber una diferencia en las puntuaciones obtenidas entre LogisticRegression con solver=liblinear o LinearSVC y la librería externa liblinear directamente, cuando fit_intercept=False y el ajuste coef_ (o) los datos a predecir son ceros. Esto se debe a que para la(s) muestra(s) con decision_function cero, LogisticRegression y LinearSVC predicen la clase negativa, mientras que liblinear predice la clase positiva. Tenga en cuenta que un modelo con fit_intercept=False y que tiene muchas muestras con decision_function cero, es probable que sea un modelo mal ajustado y se aconseja establecer fit_intercept=True y aumentar el intercept_scaling.

Nota

Selección de características con regresión logística dispersa

Una regresión logística con penalización \(\ell_1\) produce modelos dispersos, y por lo tanto puede ser utilizada para realizar la selección de características, como se detalla en Selección de características basada en L1.

Nota

Estimación del valor p

Es posible obtener los valores p y los intervalos de confianza de los coeficientes en los casos de regresión sin penalidad. El paquete statsmodels <https://pypi.org/project/statsmodels/> soporta esto de forma nativa. Dentro de sklearn, uno podría utilizar bootstrapping en su lugar también.

LogisticRegressionCV implementa la Regresión Logística con soporte de validación cruzada incorporado, para encontrar los parámetros óptimos C y l1_ratio según el atributo scoring. Los solucionadores «newton-cg», «sag», «saga» y «lbfgs» son más rápidos para los datos densos de alta dimensión, debido al arranque en caliente (ver Glosario).

Referencias:

5

Christopher M. Bishop: Pattern Recognition and Machine Learning, Chapter 4.3.4

6

Mark Schmidt, Nicolas Le Roux, and Francis Bach: Minimizing Finite Sums with the Stochastic Average Gradient.

7

Aaron Defazio, Francis Bach, Simon Lacoste-Julien: SAGA: A Fast Incremental Gradient Method With Support for Non-Strongly Convex Composite Objectives.

8

https://en.wikipedia.org/wiki/Broyden%E2%80%93Fletcher%E2%80%93Goldfarb%E2%80%93Shanno_algorithm

9

«Performance Evaluation of Lbfgs vs other solvers»

1.1.12. Regresión lineal generalizada

Los modelos lineales generalizados (GLM) amplían los modelos lineales de dos maneras 10. En primer lugar, los valores predichos \(hat{y}\) están vinculados a una combinación lineal de las variables de entrada \(X\) a través de una función de enlace inversa \(h\) como

\[\hat{y}(w, X) = h(Xw).\]

En segundo lugar, la función de pérdida al cuadrado se sustituye por la desviación unitaria \(d\) de una distribución de la familia exponencial (o más exactamente, un modelo de dispersión exponencial reproductiva (EDM) 11).

El problema de minimización se convierte en:

\[\min_{w} \frac{1}{2 n_{\text{samples}}} \sum_i d(y_i, \hat{y}_i) + \frac{\alpha}{2} ||w||_2,\]

donde \(\alpha\) es la penalización de regularización L2. Cuando se proporcionan los pesos de la muestra, la media se convierte en una media promedio.

La siguiente tabla enumera algunas EDM específicas y su desviación unitaria (todas ellas son instancias de la familia Tweedie):

Distribución	Dominio objetivo	Desviación unitaria \(d(y, \hat{y})\)
Normal	\(y \in (-\infty, \infty)\)	\((y-\hat{y})^2\)
Poisson	\(y \in [0, \infty)\)	\(2(y\log\frac{y}{\hat{y}}-y+\hat{y})\)
Gamma	\(y \in (0, \infty)\)	\(2(\log\frac{\hat{y}}{y}+\frac{y}{\hat{y}}-1)\)
Gaussiana inversa	\(y \in (0, \infty)\)	\(\frac{(y-\hat{y})^2}{y\hat{y}^2}\)

Las Funciones de Densidad de Probabilidad (PDF) de estas distribuciones se ilustran en la siguiente figura,

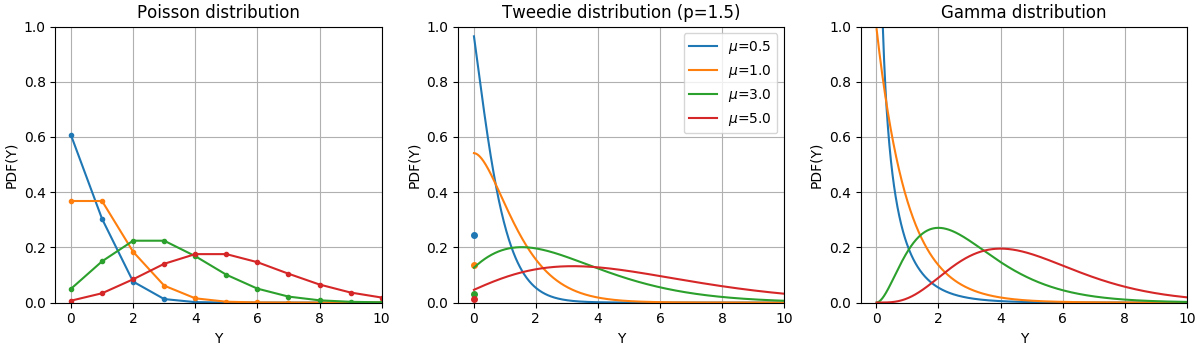
PDF de una variable aleatoria Y que sigue las distribuciones Poisson, Tweedie (potencia=1,5) y Gamma con diferentes valores medios (\(\mu\)). Observa la masa puntual en \(Y=0\) para la distribución de Poisson y la de Tweedie (potencia=1,5), pero no para la distribución Gamma que tiene un dominio objetivo estrictamente positivo.

La elección de la distribución depende del problema en cuestión:

• Si los valores objetivo \(y\) son recuentos (con valor entero no negativo) o frecuencias relativas (no negativas), podrías utilizar una desviación de Poisson con enlace log.

• Si los valores objetivo tienen un valor positivo y son asimétricos, puedes probar una desviación Gamma con enlace logarítmico.

• Si los valores objetivo parecen tener una cola más pesada que la de una distribución Gamma, podrías probar con una desviación Gaussiana Inversa (o incluso con las potencias de varianza más altas de la familia Tweedie).

Algunos ejemplos de casos de uso son:

• Agricultura / modelización meteorológica: número de eventos de lluvia por año (Poisson), cantidad de lluvia por evento (Gamma), lluvia total por año (Tweedie / Compuesta Poisson Gamma).

• Modelización de riesgos / tarificación de pólizas de seguros: número de siniestros / asegurado al año (Poisson), costo por siniestro (Gamma), costo total por asegurado al año (Tweedie / Compuesta Poisson Gamma).

• Mantenimiento predictivo: número de eventos de interrupción de la producción por año (Poisson), duración de la interrupción (Gamma), tiempo total de interrupción por año (Tweedie / Compuesta Poisson Gamma).

Referencias:

10

McCullagh, Peter; Nelder, John (1989). Generalized Linear Models, Segunda Edición. Boca Raton: Chapman and Hall/CRC. ISBN 0-412-31760-5.

11

Jørgensen, B. (1992). The theory of exponential dispersion models and analysis of deviance. Monografias de matemática, no. 51. See also Exponential dispersion model.

1.1.12.1. Uso

TweedieRegressor implementa un modelo lineal generalizado para la distribución de Tweedie, que permite modelar cualquiera de las distribuciones mencionadas utilizando el parámetro power apropiado. En particular:

• power = 0: Distribución normal. Los estimadores específicos como Ridge, ElasticNet suelen ser más apropiados en este caso.

• power = 1: Distribución de Poisson. PoissonRegressor se expone por comodidad. Sin embargo, es estrictamente equivalente a TweedieRegressor(power=1, link='log').

• potencia = 2``: La distribución Gamma. GammaRegressor se expone por conveniencia. Sin embargo, es estrictamente equivalente a TweedieRegressor(power=2, link='log').

• poder = 3: Distribución Gaussiana Inversa.

La función de enlace está determinada por el parámetro link.

Ejemplo de uso:

>>> from sklearn.linear_model import TweedieRegressor
>>> reg = TweedieRegressor(power=1, alpha=0.5, link='log')
>>> reg.fit([[0, 0], [0, 1], [2, 2]], [0, 1, 2])
TweedieRegressor(alpha=0.5, link='log', power=1)
>>> reg.coef_
array([0.2463..., 0.4337...])
>>> reg.intercept_
-0.7638...

Ejemplos:

• Regresión de Poisson y pérdida no normal

• Regresión de Tweedie en los reclamos de seguros

1.1.12.2. Consideraciones prácticas

La matriz de características X debe normalizarse antes del ajuste. Esto asegura que la penalización trata las características por igual.

Como el predictor lineal \(Xw\) puede ser negativo y las distribuciones Poisson, Gamma y Gaussiana Inversa no admiten valores negativos, es necesario aplicar una función de enlace inversa que garantice la no negatividad. Por ejemplo, con link='log', la función de enlace inversa se convierte en \(h(Xw)=\exp(Xw)\).

Si deseas modelar una frecuencia relativa, es decir, recuentos por exposición (tiempo, volumen, …) puedes hacerlo utilizando una distribución de Poisson y pasando \(y=\frac{mathrm{counts}}{\mathrm{exposure}}\) como valores objetivo junto con \(\mathrm{exposure}\) como ponderaciones de la muestra. Para un ejemplo concreto, ver: Regresión de Tweedie en los reclamos de seguros.

Cuando se realiza una validación cruzada para el parámetro power de TweedieRegressor, es aconsejable especificar una función de puntuación explícita, ya que el puntuador predeterminado TweedieRegressor.score es una función de la propia power.

1.1.13. Descenso de gradiente estocástico - SGD

El descenso de gradiente estocástico es un método sencillo pero muy eficaz para ajustar modelos lineales. Es especialmente útil cuando el número de muestras (y el número de características) es muy grande. El método partial_fit permite el aprendizaje en línea y fuera del núcleo.

Las clases SGDClassifier y SGDRegressor proporcionan funcionalidad para ajustar modelos lineales de clasificación y regresión utilizando diferentes funciones de pérdida (convexas) y diferentes penalizaciones. Por ejemplo, con loss="log", SGDClassifier se ajusta a un modelo de regresión logística, mientras que con loss="hinge" se ajusta a una máquina lineal de vectores de soporte (SVM).

Referencias

• Descenso de Gradiente Estocástico

1.1.14. Perceptrón

El Perceptron es otro algoritmo de clasificación simple adecuado para el aprendizaje a gran escala. Por defecto:

• No requiere una tasa de aprendizaje.

• No está regularizado (penalizado).

• Actualiza su modelo sólo en caso de error.

La última característica implica que el Perceptrón es ligeramente más rápido de entrenar que el SGD con la pérdida de bisagra y que los modelos resultantes son más dispersos.

1.1.15. Algoritmos pasivo-agresivos

Los algoritmos pasivo-agresivos son una familia de algoritmos para el aprendizaje a gran escala. Son similares al Perceptrón en el sentido de que no requieren una tasa de aprendizaje. Sin embargo, a diferencia del Perceptrón, incluyen un parámetro de regularización C.

Para la clasificación, PassiveAggressiveClassifier puede utilizarse con loss='hinge' (PA-I) o loss='squared_hinge' (PA-II). Para la regresión, PassiveAggressiveRegressor puede utilizarse con loss='epsilon_insensitive' (PA-I) o loss='squared_epsilon_insensitive' (PA-II).

Referencias:

• «Online Passive-Aggressive Algorithms» K. Crammer, O. Dekel, J. Keshat, S. Shalev-Shwartz, Y. Singer - JMLR 7 (2006)

1.1.16. Regresión robusta: valores atípicos y errores de modelización,

La regresión robusta tiene como objetivo ajustar un modelo de regresión en presencia de datos corruptos: ya sean valores atípicos o errores en el modelo.

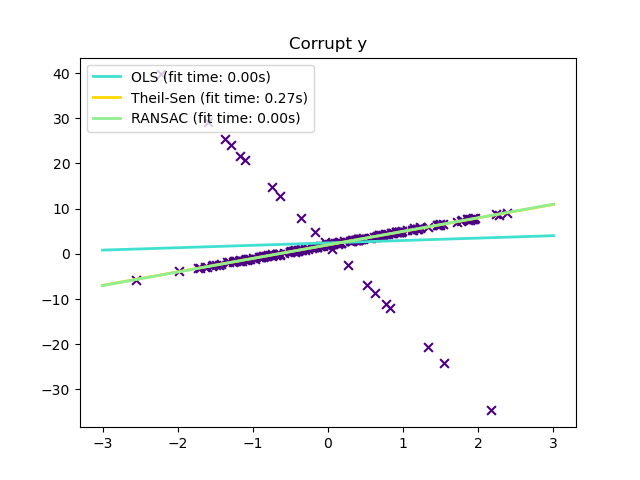
1.1.16.1. Diferentes escenarios y conceptos útiles

Hay diferentes cosas que hay que tener en cuenta cuando se trata de datos corruptos por valores atípicos:

• ¿Valores atípicos en X o en y?

  Valores atípicos en la dirección y	Valores atípicos en la dirección X

• Fracción de valores atípicos frente a la amplitud del error

  El número de puntos atípicos es importante, pero también lo son los valores atípicos.

  Valores atípicos pequeños	Valores atípicos grandes

Una noción importante de adecuación robusta es la del punto de desintegración: la fracción de los datos que pueden estar alejados para que puedan empezar a faltar los datos inminentes.

Ten en cuenta que, en general, el ajuste robusto en un entorno de alta dimensión (grande n_features) es muy difícil. Los modelos robustos aquí probablemente no funcionarán en estos escenarios.

En balance: ¿cuál estimador?

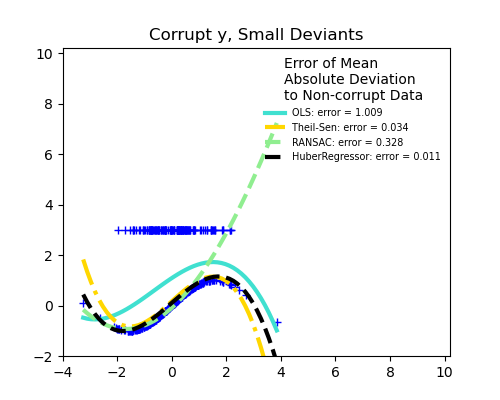
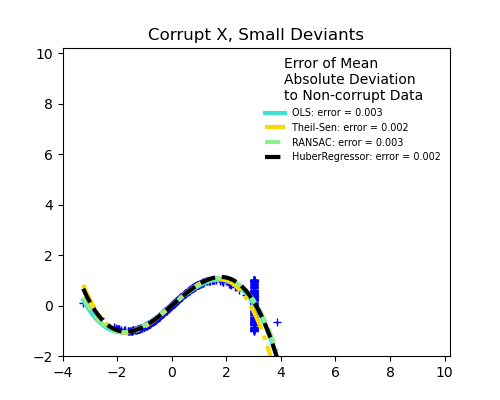
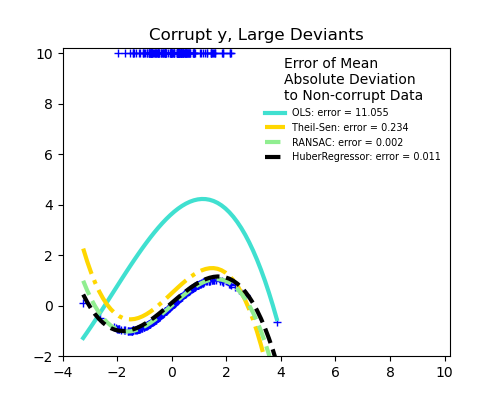
Scikit-learn provides 3 robust regression estimators: RANSAC, Theil Sen and HuberRegressor.

• HuberRegressor debería ser más rápido que RANSAC y Theil Sen a menos que el número de muestras sea muy grande, es decir, n_samples >> n_features. Esto se debe a que RANSAC y Theil Sen se ajustan a subconjuntos más pequeños de los datos. Sin embargo, tanto Theil Sen como RANSAC probablemente no sean tan robustos como HuberRegressor para los parámetros predeterminados.

• RANSAC es más rápido que Theil Sen y se escala mucho mejor con el número de muestras.

• RANSAC se ocupará mejor de los valores atípicos grandes en la dirección y (la situación más común).

• Theil Sen se ocupará mejor de los valores atípicos de tamaño medio en la dirección X, pero esta propiedad desaparecerá en entornos de alta dimensión.

En caso de duda, utilice RANSAC.

1.1.16.2. RANSAC: Consenso RANdom SAmple

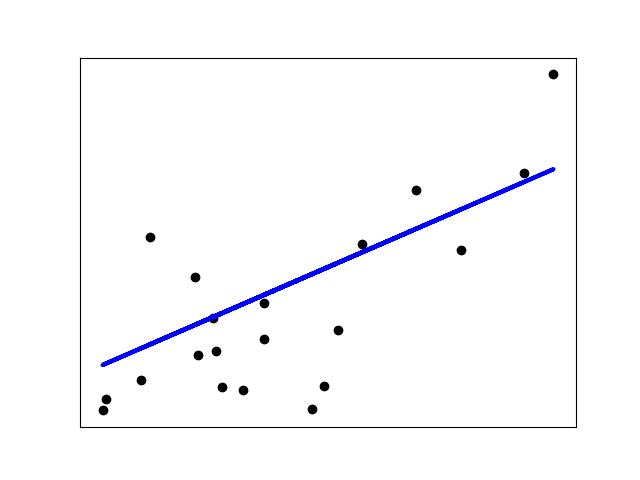
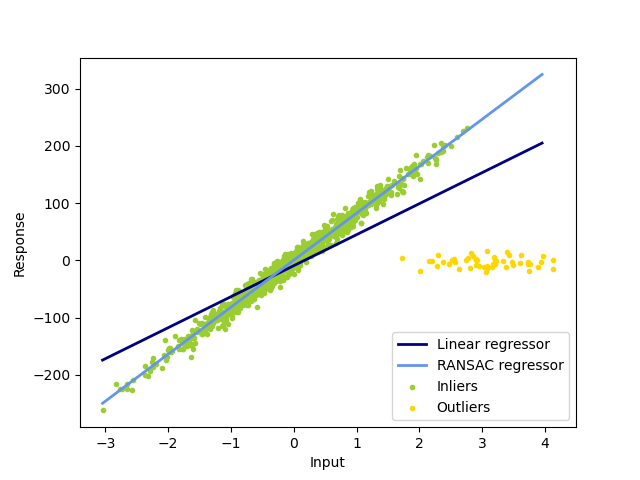
RANSAC (RANdom SAmple Consensus) ajusta un modelo a partir de subconjuntos aleatorios de valores típicos del conjunto completo de datos.

RANSAC es un algoritmo no determinista que sólo produce un resultado razonable con una cierta probabilidad, que depende del número de iteraciones (ver el parámetro max_trials). Se suele utilizar para problemas de regresión lineal y no lineal y es especialmente popular en el campo de la visión fotogramétrica por computadora.

El algoritmo divide los datos completos de la muestra de entrada en un conjunto de valores típicos, que pueden estar sujetos a ruido, y valores atípicos, que están causados, por ejemplo, por mediciones erróneas o hipótesis no válidas sobre los datos. A continuación, el modelo resultante se estima sólo a partir de los valores típicos determinados.

1.1.16.2.1. Detalles del algoritmo

Cada iteración realiza los siguientes pasos:

1. Seleccionar muestras aleatorias min_samples de los datos originales y comprobar si el conjunto de datos es válido (ver is_data_valid).

2. Ajustar un modelo al subconjunto aleatorio (base_estimator.fit) y comprobar si el modelo estimado es válido (ver is_model_valid).

3. Clasificar todos los datos como valores típicos o valores atípicos calculando los residuos del modelo estimado (base_estimator.predict(X) - y) - todas las muestras de datos con residuos absolutos menores que el residual_threshold se consideran valores atipicos.

4. Guarda el modelo ajustado como el mejor modelo si el número de muestras de valores típicos es máximo. En caso de que el modelo estimado actual tenga el mismo número de valores típicos, sólo se considera como el mejor modelo si tiene mejor puntuación.

Estos pasos se realizan un número máximo de veces (max_trials) o hasta que se cumpla uno de los criterios especiales de parada (ver stop_n_inliers y stop_score). El modelo final se estima utilizando todas las muestras de valores típicos (conjunto de consenso) del mejor modelo determinado previamente.

Las funciones is_data_valid y is_model_valid permiten identificar y rechazar combinaciones degeneradas de submuestras aleatorias. Si no se necesita el modelo estimado para identificar los casos degenerados, debería utilizarse is_data_valid, ya que se llama antes de ajustar el modelo y, por tanto, se obtiene un mejor rendimiento computacional.

Ejemplos:

• Estimación robusta de modelos lineales mediante RANSAC

• Ajuste del estimador lineal robusto

Referencias:

• https://es.wikipedia.org/wiki/RANSAC

• «Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography» Martin A. Fischler y Robert C. Bolles - SRI International (1981)

• «Performance Evaluation of RANSAC Family» Sunglok Choi, Taemin Kim and Wonpil Yu - BMVC (2009)

1.1.16.3. Estimador Theil-Sen: estimador basado en la mediana generalizada

El estimador TheilSenRegressor utiliza una generalización de la mediana en múltiples dimensiones. Por lo tanto, es robusto a los valores atípicos multivariados. Sin embargo, la robustez del estimador disminuye rápidamente con la dimensionalidad del problema. Pierde sus propiedades de robustez y no es mejor que un mínimo cuadrado ordinario en una dimensión alta.

Ejemplos:

• Regresión de Theil-Sen

• Ajuste del estimador lineal robusto

Referencias:

• https://en.wikipedia.org/wiki/Theil%E2%80%93Sen_estimator

1.1.16.3.1. Consideraciones teóricas

TheilSenRegressor es comparable al Mínimos cuadrados ordinarios (OLS) en términos de eficiencia asintótica y como estimador insesgado. En contraste con OLS, Theil-Sen es un método no paramétrico, lo que significa que no hace ninguna suposición sobre la distribución subyacente de los datos. Dado que Theil-Sen es un estimador basado en la mediana, es más robusto frente a los datos corruptos y los valores atípicos. En un entorno univariante, Theil-Sen tiene un punto de ruptura de aproximadamente el 29,3% en el caso de una regresión lineal simple, lo que significa que puede tolerar datos corruptos arbitrarios de hasta el 29,3%.

La implementación de TheilSenRegressor en scikit-learn sigue una generalización a un modelo de regresión lineal multivariante 12 utilizando la mediana espacial que es una generalización de la mediana a múltiples dimensiones 13.

En términos de complejidad temporal y espacial, Theil-Sen escala según

\[\binom{n_{\text{samples}}}{n_{\text{subsamples}}}\]

lo que hace inviable su aplicación exhaustiva a problemas con un gran número de muestras y características. Por lo tanto, la magnitud de una subpoblación puede elegirse para limitar la complejidad temporal y espacial considerando sólo un subconjunto aleatorio de todas las combinaciones posibles.

Ejemplos:

• Regresión de Theil-Sen

Referencias:

12

Xin Dang, Hanxiang Peng, Xueqin Wang and Heping Zhang: Theil-Sen Estimators in a Multiple Linear Regression Model.

13

20. Kärkkäinen and S. Äyrämö: On Computation of Spatial Median for Robust Data Mining.

1.1.16.4. Regresión Huber

El HuberRegressor es diferente al Ridge porque aplica una pérdida lineal a las muestras que se clasifican como valores atípicos. Una muestra se clasifica como un valor típico si el error absoluto de esa muestra es menor que un determinado umbral. Se diferencia de TheilSenRegressor y de RANSACRegressor porque no ignora el efecto de los valores atípicos sino que les da un peso menor.

La función de pérdida que minimiza HuberRegressor viene dada por

\[\min_{w, \sigma} {\sum_{i=1}^n\left(\sigma + H_{\epsilon}\left(\frac{X_{i}w - y_{i}}{\sigma}\right)\sigma\right) + \alpha {||w||_2}^2}\]

donde

\[\begin{split}H_{\epsilon}(z) = \begin{cases} z^2, & \text {if } |z| < \epsilon, \\ 2\epsilon|z| - \epsilon^2, & \text{otherwise} \end{cases}\end{split}\]

Se aconseja ajustar el parámetro epsilon a 1,35 para conseguir una eficacia estadística del 95%.

1.1.16.5. Notas

El HuberRegressor difiere del uso de SGDRegressor con la pérdida establecida en huber en los siguientes aspectos.

• HuberRegressor es invariante de la escala. Una vez que epsilon se establece, escalando X y y por diferentes valores produciría la misma robustez a los valores atípicos como antes. en comparación con SGDRegressor donde epsilon tiene que ser establecido de nuevo cuando X y y se escalan.

• HuberRegressor debería ser más eficiente para usar en datos con un pequeño número de muestras mientras que SGDRegressor necesita varias pasadas en los datos de entrenamiento para producir la misma robustez.

Ejemplos:

• HuberRegressor vs Ridge en un conjunto de datos con fuertes valores atípicos

Referencias:

• Peter J. Huber, Elvezio M. Ronchetti: Robust Statistics, Concomitant scale estimates, pg 172

Ten en cuenta que este estimador es diferente de la implementación de R de la Regresión Robusta (http://www.ats.ucla.edu/stat/r/dae/rreg.htm) porque la implementación de R hace una aplicación de mínimos cuadrados ponderados con pesos dados a cada muestra sobre la base de cuánto el residuo es mayor que un cierto umbral.

1.1.17. Regresión polinómica: ampliación de los modelos lineales con funciones de base

Un patrón común dentro del aprendizaje automático es utilizar modelos lineales entrenados en funciones no lineales de los datos. Este enfoque mantiene el rendimiento generalmente rápido de los métodos lineales, al tiempo que les permite ajustarse a una gama mucho más amplia de datos.

Por ejemplo, una regresión lineal simple puede ampliarse construyendo funciones polinómicas a partir de los coeficientes. En el caso de la regresión lineal estándar, se podría tener un modelo como este para datos bidimensionales:

\[\hat{y}(w, x) = w_0 + w_1 x_1 + w_2 x_2\]

Si queremos ajustar un paraboloide a los datos en lugar de un plano, podemos combinar las características en polinomios de segundo orden, de forma que el modelo tenga este aspecto:

\[\hat{y}(w, x) = w_0 + w_1 x_1 + w_2 x_2 + w_3 x_1 x_2 + w_4 x_1^2 + w_5 x_2^2\]

La observación (a veces sorprendente) es que éste es un modelo lineal: para verlo, imaginemos que creamos un nuevo conjunto de características

\[z = [x_1, x_2, x_1 x_2, x_1^2, x_2^2]\]

Con este reetiquetado de los datos, nuestro problema se puede escribir

\[\hat{y}(w, z) = w_0 + w_1 z_1 + w_2 z_2 + w_3 z_3 + w_4 z_4 + w_5 z_5\]

Vemos que la regresión polinómica resultante pertenece a la misma clase de modelos lineales que hemos considerado anteriormente (es decir, el modelo es lineal en \(w\)) y puede resolverse con las mismas técnicas. Al considerar los ajustes lineales dentro de un espacio de mayor dimensión construido con estas funciones base, el modelo tiene la flexibilidad de ajustarse a una gama de datos mucho más amplia.

He aquí un ejemplo de aplicación de esta idea a datos unidimensionales, utilizando funciones polinómicas de distintos grados:

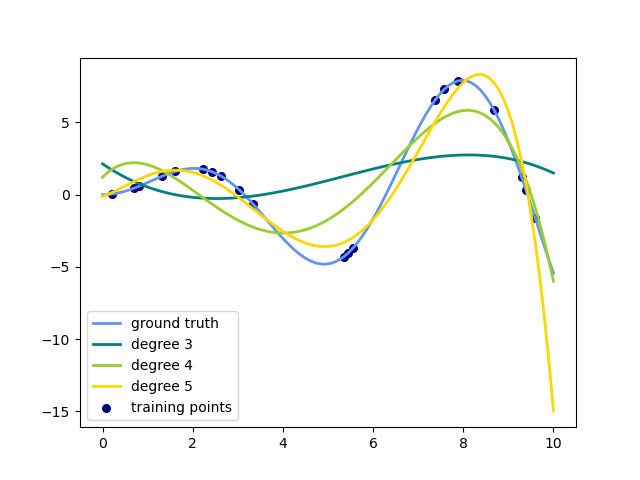
Esta figura se crea utilizando el transformador PolynomialFeatures, que transforma una matriz de datos de entrada en una nueva matriz de datos de un grado determinado. Se puede utilizar de la siguiente manera:

>>> from sklearn.preprocessing import PolynomialFeatures
>>> import numpy as np
>>> X = np.arange(6).reshape(3, 2)
>>> X
array([[0, 1],
       [2, 3],
       [4, 5]])
>>> poly = PolynomialFeatures(degree=2)
>>> poly.fit_transform(X)
array([[ 1.,  0.,  1.,  0.,  0.,  1.],
       [ 1.,  2.,  3.,  4.,  6.,  9.],
       [ 1.,  4.,  5., 16., 20., 25.]])

Las características de X se han transformado de \([x_1, x_2]\) a \([1, x_1, x_2, x_1^2, x_1 x_2, x_2^2]\), y ahora pueden utilizarse dentro de cualquier modelo lineal.

Este tipo de preprocesamiento puede agilizarse con las herramientas Pipeline. Un único objeto que representa una regresión polinómica simple puede crearse y utilizarse de la siguiente manera:

>>> from sklearn.preprocessing import PolynomialFeatures
>>> from sklearn.linear_model import LinearRegression
>>> from sklearn.pipeline import Pipeline
>>> import numpy as np
>>> model = Pipeline([('poly', PolynomialFeatures(degree=3)),
...                   ('linear', LinearRegression(fit_intercept=False))])
>>> # fit to an order-3 polynomial data
>>> x = np.arange(5)
>>> y = 3 - 2 * x + x ** 2 - x ** 3
>>> model = model.fit(x[:, np.newaxis], y)
>>> model.named_steps['linear'].coef_
array([ 3., -2.,  1., -1.])

El modelo lineal entrenado en características polinómicas es capaz de recuperar exactamente los coeficientes polinómicos de entrada.

En algunos casos no es necesario incluir las potencias más altas de ninguna característica, sino sólo las llamadas características de interacción que multiplican a lo sumo \(d\) características distintas. Estas pueden obtenerse de PolynomialFeatures con el ajuste interaction_only=True.

Por ejemplo, cuando se trata de características booleanas, \(x_i^n = x_i\) para todos los \(n\) y, por tanto, es inútil; pero \(x_i x_j\) representa la conjunción de dos booleanos. De este modo, podemos resolver el problema XOR con un clasificador lineal:

>>> from sklearn.linear_model import Perceptron
>>> from sklearn.preprocessing import PolynomialFeatures
>>> import numpy as np
>>> X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
>>> y = X[:, 0] ^ X[:, 1]
>>> y
array([0, 1, 1, 0])
>>> X = PolynomialFeatures(interaction_only=True).fit_transform(X).astype(int)
>>> X
array([[1, 0, 0, 0],
       [1, 0, 1, 0],
       [1, 1, 0, 0],
       [1, 1, 1, 1]])
>>> clf = Perceptron(fit_intercept=False, max_iter=10, tol=None,
...                  shuffle=False).fit(X, y)

Y las «predicciones» del clasificador son perfectas:

>>> clf.predict(X)
array([0, 1, 1, 0])
>>> clf.score(X, y)
1.0