Nota
Haz clic aquí para descargar el código completo del ejemplo o para ejecutar este ejemplo en tu navegador a través de Binder
Errores comunes en la interpretación de los coeficientes de los modelos lineales¶
En los modelos lineales, el valor objetivo se modela como una combinación lineal de las características (consulta la sección del Manual de Usuario Modelos lineales para una descripción de un conjunto de modelos lineales disponibles en scikit-learn). Los coeficientes en los modelos lineales múltiples representan la relación entre la característica dada, \(X_i\) y el objetivo, \(y\), asumiendo que todas las demás características permanecen constantes (dependencia condicional). Esto es diferente de graficar \(X_i\) versus \(y\) y ajustar una relación lineal: en ese caso todos los valores posibles de las otras características se tienen en cuenta en la estimación (dependencia marginal).
Este ejemplo proporcionará algunas pistas para interpretar los coeficientes en los modelos lineales, señalando los problemas que surgen cuando el modelo lineal no es apropiado para describir el conjunto de datos o cuando las características están correlacionadas.
Utilizaremos datos de la «Current Population Survey» de 1985 para predecir el salario en función de diversas características como la experiencia, la edad o la educación.
print(__doc__)
import numpy as np
import scipy as sp
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
El conjunto de datos: salarios (wages)¶
Obtenemos los datos de OpenML. Ten en cuenta que al establecer el parámetro as_frame en True se recuperarán los datos como un dataframe de pandas.
from sklearn.datasets import fetch_openml
survey = fetch_openml(data_id=534, as_frame=True)
Luego, identificamos las características X y los objetivos y: la columna WAGE es nuestra variable objetivo (es decir, la variable que queremos predecir).
X = survey.data[survey.feature_names]
X.describe(include="all")
Ten en cuenta que el conjunto de datos contiene variables categóricas y numéricas. Tendremos que tener esto en cuenta al preprocesar el conjunto de datos a partir de entonces.
X.head()
Nuestro objetivo de predicción: el salario. Los salarios se describen como un número de punto flotante en dólares por hora.
y = survey.target.values.ravel()
survey.target.head()
Out:
0 5.10
1 4.95
2 6.67
3 4.00
4 7.50
Name: WAGE, dtype: float64
Dividimos la muestra en un conjunto de datos de entrenamiento y otro de prueba. En el siguiente análisis exploratorio sólo se utilizará el conjunto de datos de entrenamiento. Esta es una forma de emular una situación real en la que las predicciones se realizan sobre un objetivo desconocido, y no queremos que nuestros análisis y decisiones estén sesgados por nuestro conocimiento de los datos de prueba.
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
X, y, random_state=42
)
Primero, obtengamos algunas ideas observando las distribuciones de las variables y las relaciones por pares entre ellas. Sólo se utilizarán variables numéricas. En el siguiente gráfico, cada punto representa una muestra.
train_dataset = X_train.copy()
train_dataset.insert(0, "WAGE", y_train)
_ = sns.pairplot(train_dataset, kind='reg', diag_kind='kde')
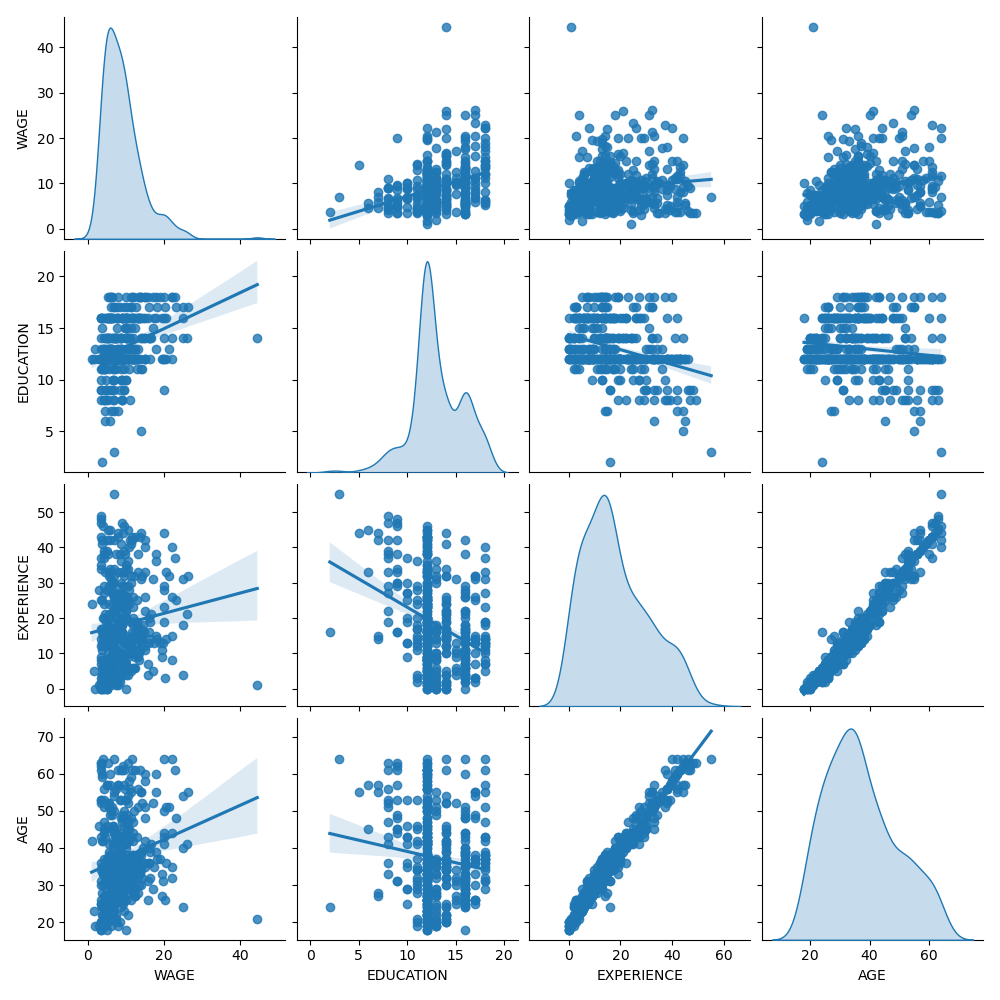
Si observamos detenidamente la distribución del salario (WAGE), veremos que tiene una cola larga. Por ello, debemos tomar su logaritmo para convertirla aproximadamente en una distribución normal (los modelos lineales como el cresta o el lasso funcionan mejor para una distribución normal del error).
El salario (WAGE) es creciente cuando la educación (EDUCATION) es creciente. Ten en cuenta que la dependencia entre WAGE y EDUCATION representada aquí es una dependencia marginal, es decir, describe el comportamiento de una variable específica sin mantener fijas las demás.
Además, la experiencia (EXPERIENCE) y la edad (AGE) están fuertemente correlacionadas de forma lineal.
El pipeline del aprendizaje automático¶
Para diseñar nuestro pipeline de aprendizaje automático, primero comprobamos manualmente el tipo de datos con los que estamos tratando:
survey.data.info()
Out:
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 534 entries, 0 to 533
Data columns (total 10 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 EDUCATION 534 non-null float64
1 SOUTH 534 non-null category
2 SEX 534 non-null category
3 EXPERIENCE 534 non-null float64
4 UNION 534 non-null category
5 AGE 534 non-null float64
6 RACE 534 non-null category
7 OCCUPATION 534 non-null category
8 SECTOR 534 non-null category
9 MARR 534 non-null category
dtypes: category(7), float64(3)
memory usage: 17.2 KB
Como se ha visto anteriormente, el conjunto de datos contiene columnas con diferentes tipos de datos y tenemos que aplicar un preprocesamiento específico para cada tipo de datos. En particular, las variables categóricas no pueden incluirse en el modelo lineal si no se codifican primero como números enteros. Además, para evitar que las características categóricas se traten como valores ordenados, necesitamos aplicarles una codificación one-hot. Nuestro preprocesador
codificará one-hot (es decir, generará una columna por categoría) las columnas categóricas;
como primer enfoque (veremos después cómo afectará la normalización de los valores numéricos a nuestra discusión), mantendrá los valores numéricos tal y como están.
from sklearn.compose import make_column_transformer
from sklearn.preprocessing import OneHotEncoder
categorical_columns = ['RACE', 'OCCUPATION', 'SECTOR',
'MARR', 'UNION', 'SEX', 'SOUTH']
numerical_columns = ['EDUCATION', 'EXPERIENCE', 'AGE']
preprocessor = make_column_transformer(
(OneHotEncoder(drop='if_binary'), categorical_columns),
remainder='passthrough'
)
Para describir el conjunto de datos como un modelo lineal utilizamos un regresor ridge (de cresta) con una regularización muy pequeña y para modelar el logaritmo del WAGE.
from sklearn.pipeline import make_pipeline
from sklearn.linear_model import Ridge
from sklearn.compose import TransformedTargetRegressor
model = make_pipeline(
preprocessor,
TransformedTargetRegressor(
regressor=Ridge(alpha=1e-10),
func=np.log10,
inverse_func=sp.special.exp10
)
)
Procesamiento del conjunto de datos¶
Primero, ajustamos el modelo.
_ = model.fit(X_train, y_train)
Luego comprobamos el rendimiento del modelo calculado graficando sus predicciones en el conjunto de pruebas y calculando, por ejemplo, la mediana del error absoluto del modelo.
from sklearn.metrics import median_absolute_error
y_pred = model.predict(X_train)
mae = median_absolute_error(y_train, y_pred)
string_score = f'MAE on training set: {mae:.2f} $/hour'
y_pred = model.predict(X_test)
mae = median_absolute_error(y_test, y_pred)
string_score += f'\nMAE on testing set: {mae:.2f} $/hour'
fig, ax = plt.subplots(figsize=(5, 5))
plt.scatter(y_test, y_pred)
ax.plot([0, 1], [0, 1], transform=ax.transAxes, ls="--", c="red")
plt.text(3, 20, string_score)
plt.title('Ridge model, small regularization')
plt.ylabel('Model predictions')
plt.xlabel('Truths')
plt.xlim([0, 27])
_ = plt.ylim([0, 27])
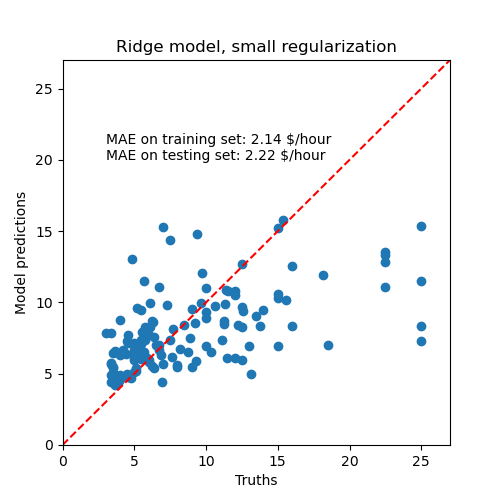
El modelo aprendido está lejos de ser un buen modelo para hacer predicciones precisas: esto es obvio al observar el gráfico anterior, donde las buenas predicciones deberían situarse en la línea roja.
En la siguiente sección, interpretaremos los coeficientes del modelo. Mientras lo hacemos, debemos tener en cuenta que cualquier conclusión que saquemos es sobre el modelo que construimos, y no sobre el verdadero proceso generativo (del mundo real) de los datos.
Interpretación de los coeficientes: la escala importa¶
En primer lugar, podemos echar un vistazo a los valores de los coeficientes del regresor que hemos ajustado.
feature_names = (model.named_steps['columntransformer']
.named_transformers_['onehotencoder']
.get_feature_names(input_features=categorical_columns))
feature_names = np.concatenate(
[feature_names, numerical_columns])
coefs = pd.DataFrame(
model.named_steps['transformedtargetregressor'].regressor_.coef_,
columns=['Coefficients'], index=feature_names
)
coefs
El coeficiente de la edad (AGE) se expresa en «dólares/hora por años de vida», mientras que el de la educación (EDUCATION) se expresa en «dólares/hora por años de educación». Esta representación de los coeficientes tiene la ventaja de dejar claras las predicciones prácticas del modelo: un aumento de \(1\) año en AGE significa una disminución de \(0,030867\) dólares/hora, mientras que un aumento de \(1\) año en EDUCATION significa un aumento de \(0,054699\) dólares/hora. Por otro lado, las variables categóricas (como UNION o SEX) son números adimensionales que toman el valor 0 o 1. Sus coeficientes se expresan en dólares/hora. Entonces, no podemos comparar la magnitud de los distintos coeficientes, ya que las características tienen escalas naturales diferentes, y por tanto rangos de valores, debido a su diferente unidad de medida. Esto es más visible si graficamos los coeficientes.
coefs.plot(kind='barh', figsize=(9, 7))
plt.title('Ridge model, small regularization')
plt.axvline(x=0, color='.5')
plt.subplots_adjust(left=.3)
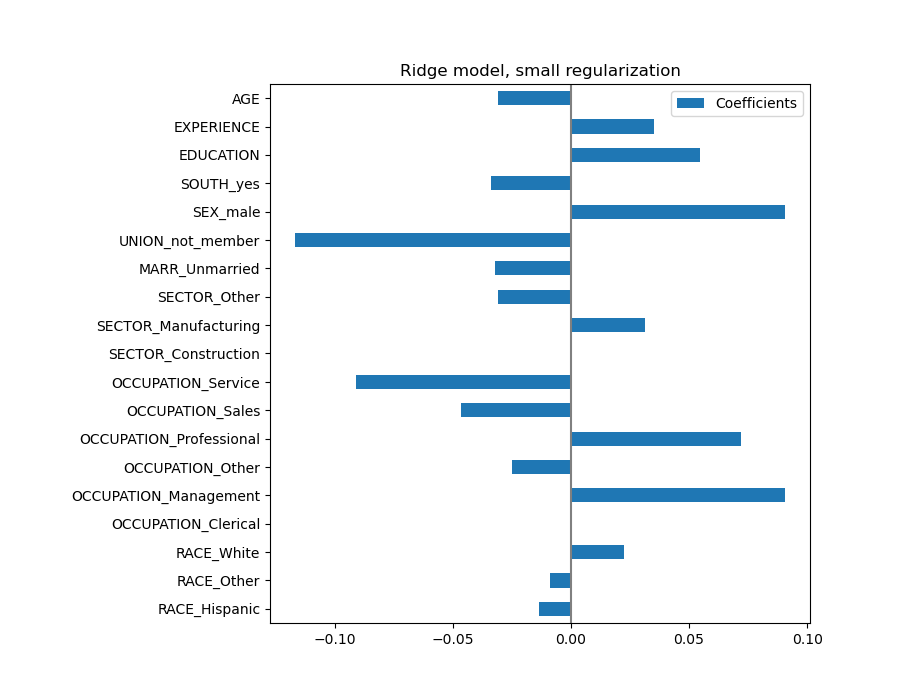
De hecho, según el gráfico anterior, el factor más importante para determinar el salario (WAGE) parece ser la variable UNION, aunque nuestra intuición nos diga que variables como EXPERIENCE deberían tener más impacto.
Observar el gráfico de coeficientes para medir la importancia de las características puede ser no representativo, ya que algunas de ellas varían a pequeña escala, mientras que otras, como AGE, varían mucho más, varias décadas.
Esto es visible si comparamos las desviaciones estándar de las diferentes características.
X_train_preprocessed = pd.DataFrame(
model.named_steps['columntransformer'].transform(X_train),
columns=feature_names
)
X_train_preprocessed.std(axis=0).plot(kind='barh', figsize=(9, 7))
plt.title('Features std. dev.')
plt.subplots_adjust(left=.3)
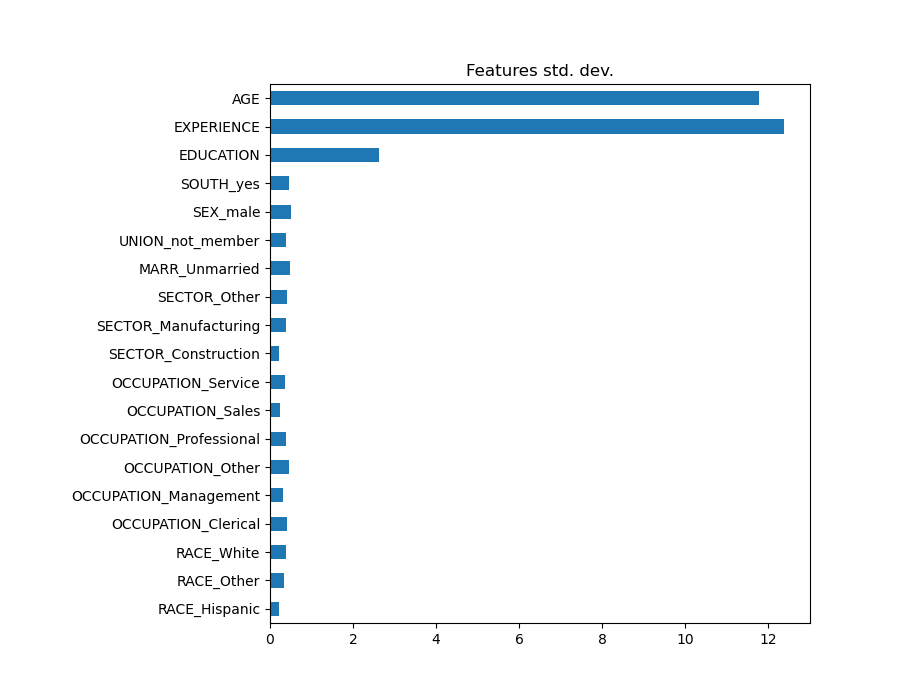
Multiplicar los coeficientes por la desviación estándar de la característica relacionada reduciría todos los coeficientes a la misma unidad de medida. Como veremos después esto equivale a normalizar las variables numéricas a su desviación estándar, como \(y = \sum{coef_i \times X_i} = \sum{(coef_i \times std_i) \times (X_i / std_i)}\).
De este modo, destacamos que cuanto mayor sea la varianza de una característica, mayor será la ponderación del coeficiente correspondiente en la salida, en igualdad de condiciones.
coefs = pd.DataFrame(
model.named_steps['transformedtargetregressor'].regressor_.coef_ *
X_train_preprocessed.std(axis=0),
columns=['Coefficient importance'], index=feature_names
)
coefs.plot(kind='barh', figsize=(9, 7))
plt.title('Ridge model, small regularization')
plt.axvline(x=0, color='.5')
plt.subplots_adjust(left=.3)
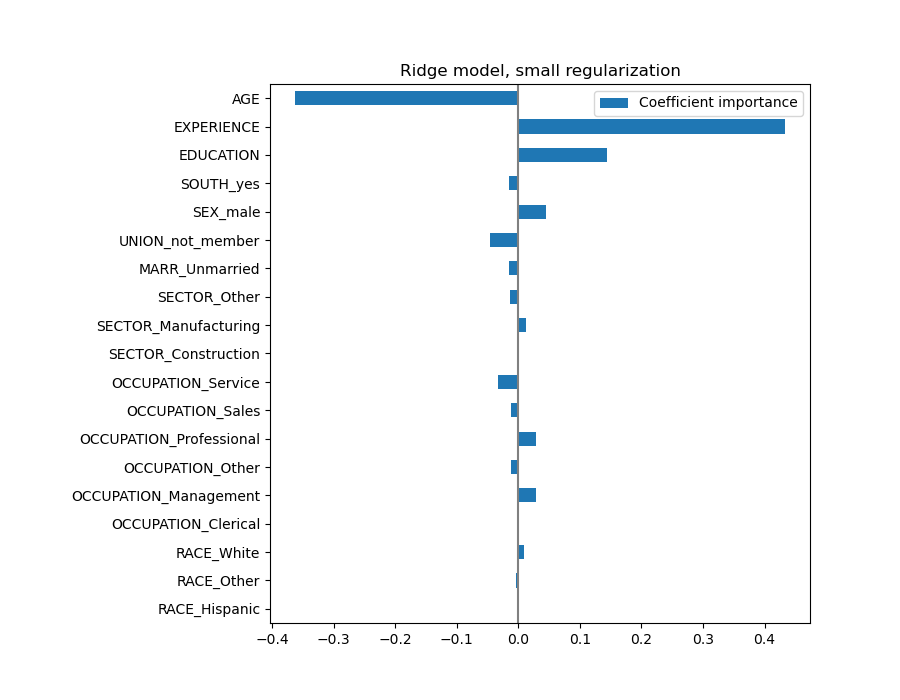
Ahora que se han escalado los coeficientes, podemos compararlos con seguridad.
Advertencia
¿Por qué el gráfico anterior sugiere que un aumento de la edad conduce a una disminución del salario? ¿Por qué el initial pairplot dice lo contrario?
El gráfico anterior nos informa sobre las dependencias entre una característica específica y el objetivo cuando todas las demás características permanecen constantes, es decir, las dependencias condicionales. Un aumento de la edad (AGE) inducirá una disminución del salario (WAGE) cuando todas las demás características permanecen constantes. Por el contrario, un aumento de la experiencia (EXPERIENCE) inducirá un aumento de WAGE cuando todas las demás características permanezcan constantes. Además, AGE, EXPERIENCE y EDUCATION son las tres variables que más influyen en el modelo.
Comprobación de la variabilidad de los coeficientes¶
Podemos comprobar la variabilidad de los coeficientes mediante la validación cruzada: es una forma de perturbación de los datos (relacionada con el remuestreo).
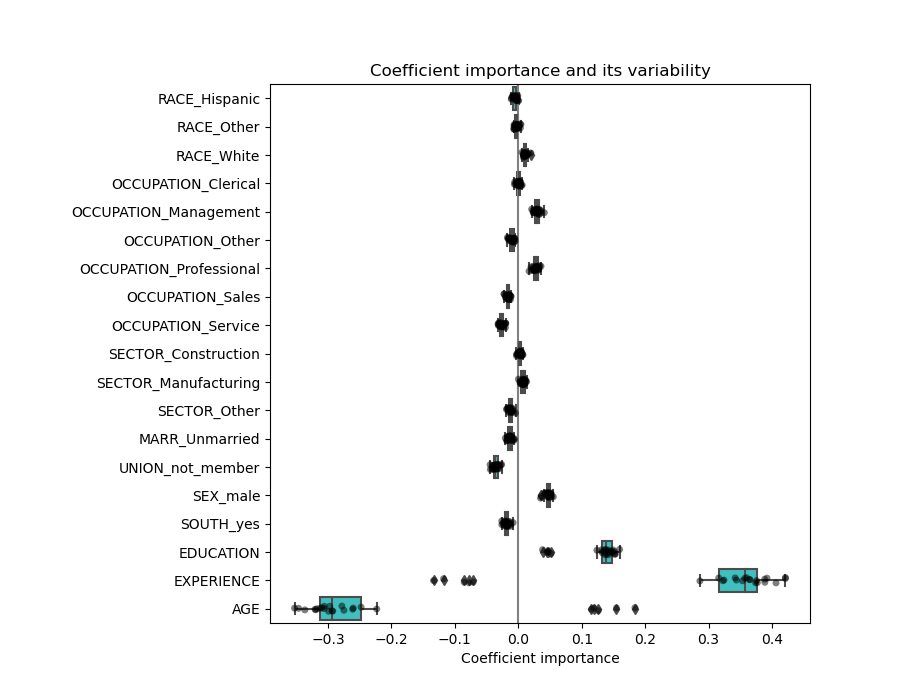
Si los coeficientes varían significativamente al cambiar el conjunto de datos de entrada, su robustez no está garantizada, y probablemente deban interpretarse con precaución.
from sklearn.model_selection import cross_validate
from sklearn.model_selection import RepeatedKFold
cv_model = cross_validate(
model, X, y, cv=RepeatedKFold(n_splits=5, n_repeats=5),
return_estimator=True, n_jobs=-1
)
coefs = pd.DataFrame(
[est.named_steps['transformedtargetregressor'].regressor_.coef_ *
X_train_preprocessed.std(axis=0)
for est in cv_model['estimator']],
columns=feature_names
)
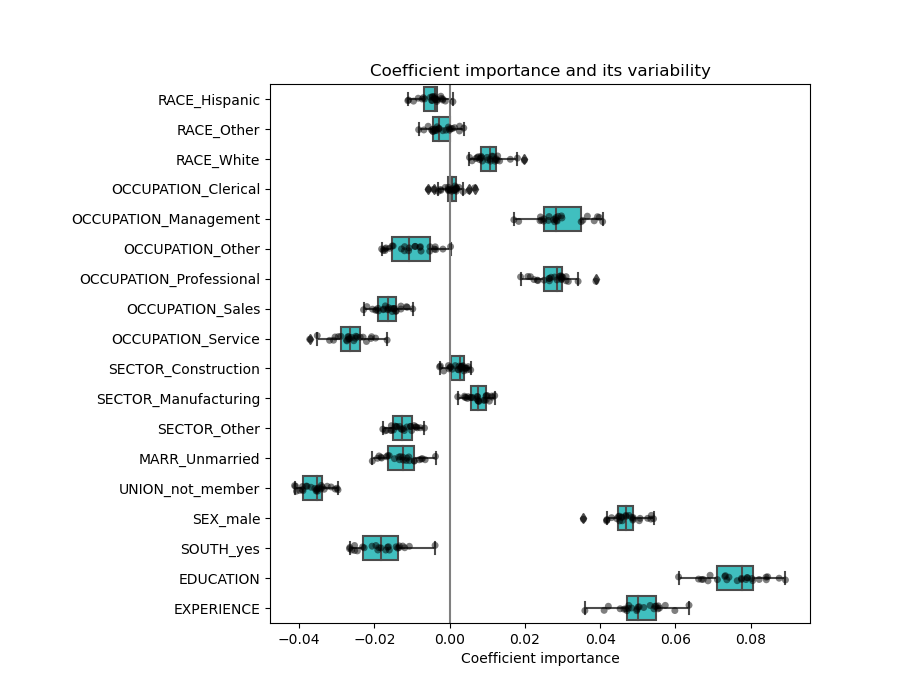
plt.figure(figsize=(9, 7))
sns.stripplot(data=coefs, orient='h', color='k', alpha=0.5)
sns.boxplot(data=coefs, orient='h', color='cyan', saturation=0.5)
plt.axvline(x=0, color='.5')
plt.xlabel('Coefficient importance')
plt.title('Coefficient importance and its variability')
plt.subplots_adjust(left=.3)
El problema de las variables correlacionadas¶
Los coeficientes de AGE y EXPERIENCE están afectados por una fuerte variabilidad que podría deberse a la colinealidad entre las dos características: como AGE y EXPERIENCE varían juntas en los datos, su efecto es difícil de separar.
Para verificar esta interpretación, graficamos la variabilidad del coeficiente de AGE y EXPERIENCE.
plt.ylabel('Age coefficient')
plt.xlabel('Experience coefficient')
plt.grid(True)
plt.xlim(-0.4, 0.5)
plt.ylim(-0.4, 0.5)
plt.scatter(coefs["AGE"], coefs["EXPERIENCE"])
_ = plt.title('Co-variations of coefficients for AGE and EXPERIENCE '
'across folds')
Dos regiones están pobladas: cuando el coeficiente de EXPERIENCE es positivo el de AGE es negativo y viceversa.
Para ir más lejos, eliminamos una de las dos características y comprobamos cuál es el impacto en la estabilidad del modelo.
column_to_drop = ['AGE']
cv_model = cross_validate(
model, X.drop(columns=column_to_drop), y,
cv=RepeatedKFold(n_splits=5, n_repeats=5),
return_estimator=True, n_jobs=-1
)
coefs = pd.DataFrame(
[est.named_steps['transformedtargetregressor'].regressor_.coef_ *
X_train_preprocessed.drop(columns=column_to_drop).std(axis=0)
for est in cv_model['estimator']],
columns=feature_names[:-1]
)
plt.figure(figsize=(9, 7))
sns.stripplot(data=coefs, orient='h', color='k', alpha=0.5)
sns.boxplot(data=coefs, orient='h', color='cyan', saturation=0.5)
plt.axvline(x=0, color='.5')
plt.title('Coefficient importance and its variability')
plt.xlabel('Coefficient importance')
plt.subplots_adjust(left=.3)
La estimación del coeficiente de EXPERIENCE es ahora menos variable y sigue siendo importante para todos los modelos entrenados durante la validación cruzada.
Preprocesamiento de variables numéricas¶
Como se dijo anteriormente (ver «El pipeline del aprendizaje automático»), también podríamos optar por escalar los valores numéricos antes de entrenar el modelo. Esto puede ser útil para aplicar una regularización de cantidad similar a todos ellos en la Cresta. El preprocesador se redefine para restar la media y escalar las variables a la varianza unitaria.
from sklearn.preprocessing import StandardScaler
preprocessor = make_column_transformer(
(OneHotEncoder(drop='if_binary'), categorical_columns),
(StandardScaler(), numerical_columns),
remainder='passthrough'
)
El modelo se mantendrá sin cambios.
model = make_pipeline(
preprocessor,
TransformedTargetRegressor(
regressor=Ridge(alpha=1e-10),
func=np.log10,
inverse_func=sp.special.exp10
)
)
_ = model.fit(X_train, y_train)
De nuevo, comprobamos el rendimiento del modelo calculado utilizando, por ejemplo, la mediana del error absoluto del modelo y el coeficiente R cuadrado.
y_pred = model.predict(X_train)
mae = median_absolute_error(y_train, y_pred)
string_score = f'MAE on training set: {mae:.2f} $/hour'
y_pred = model.predict(X_test)
mae = median_absolute_error(y_test, y_pred)
string_score += f'\nMAE on testing set: {mae:.2f} $/hour'
fig, ax = plt.subplots(figsize=(6, 6))
plt.scatter(y_test, y_pred)
ax.plot([0, 1], [0, 1], transform=ax.transAxes, ls="--", c="red")
plt.text(3, 20, string_score)
plt.title('Ridge model, small regularization, normalized variables')
plt.ylabel('Model predictions')
plt.xlabel('Truths')
plt.xlim([0, 27])
_ = plt.ylim([0, 27])
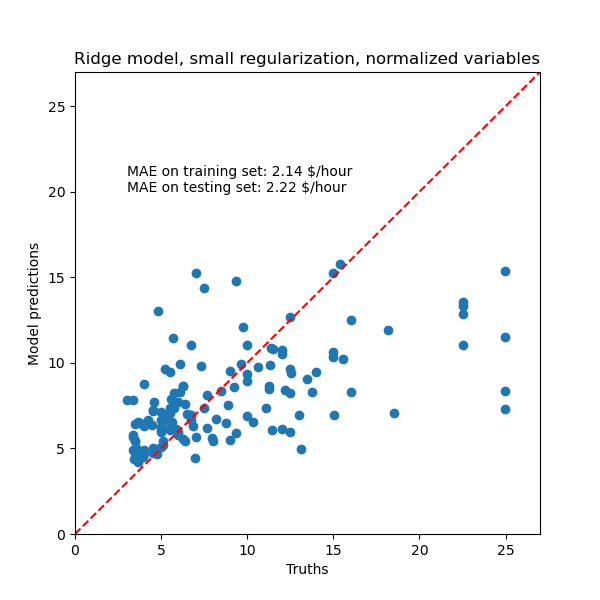
Para el análisis de los coeficientes, esta vez no es necesario el escalamiento.
coefs = pd.DataFrame(
model.named_steps['transformedtargetregressor'].regressor_.coef_,
columns=['Coefficients'], index=feature_names
)
coefs.plot(kind='barh', figsize=(9, 7))
plt.title('Ridge model, small regularization, normalized variables')
plt.axvline(x=0, color='.5')
plt.subplots_adjust(left=.3)
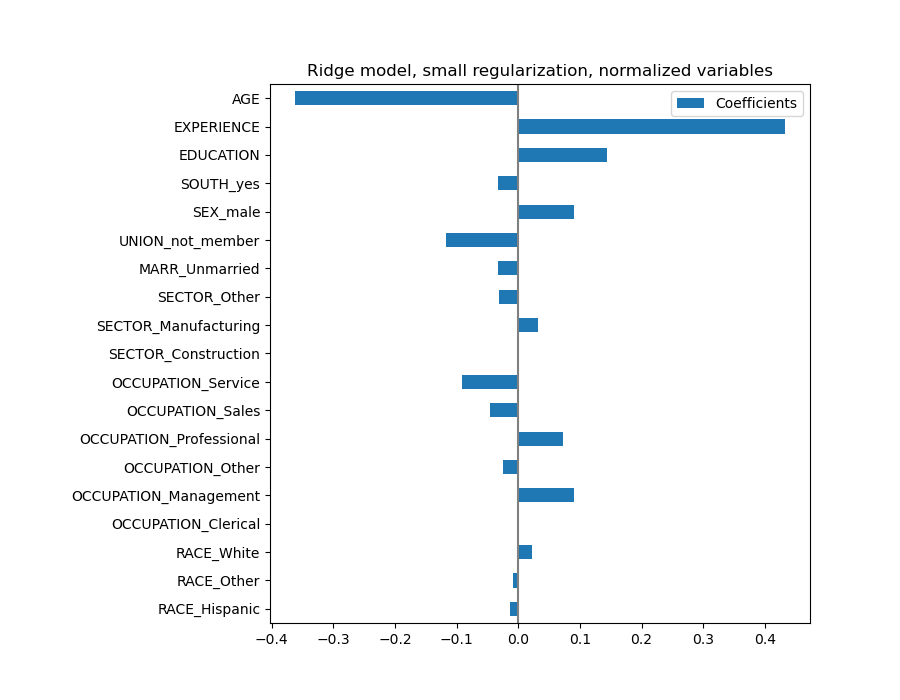
Ahora inspeccionamos los coeficientes en varios pliegues (folds) de validación cruzada.
cv_model = cross_validate(
model, X, y, cv=RepeatedKFold(n_splits=5, n_repeats=5),
return_estimator=True, n_jobs=-1
)
coefs = pd.DataFrame(
[est.named_steps['transformedtargetregressor'].regressor_.coef_
for est in cv_model['estimator']],
columns=feature_names
)
plt.figure(figsize=(9, 7))
sns.stripplot(data=coefs, orient='h', color='k', alpha=0.5)
sns.boxplot(data=coefs, orient='h', color='cyan', saturation=0.5)
plt.axvline(x=0, color='.5')
plt.title('Coefficient variability')
plt.subplots_adjust(left=.3)
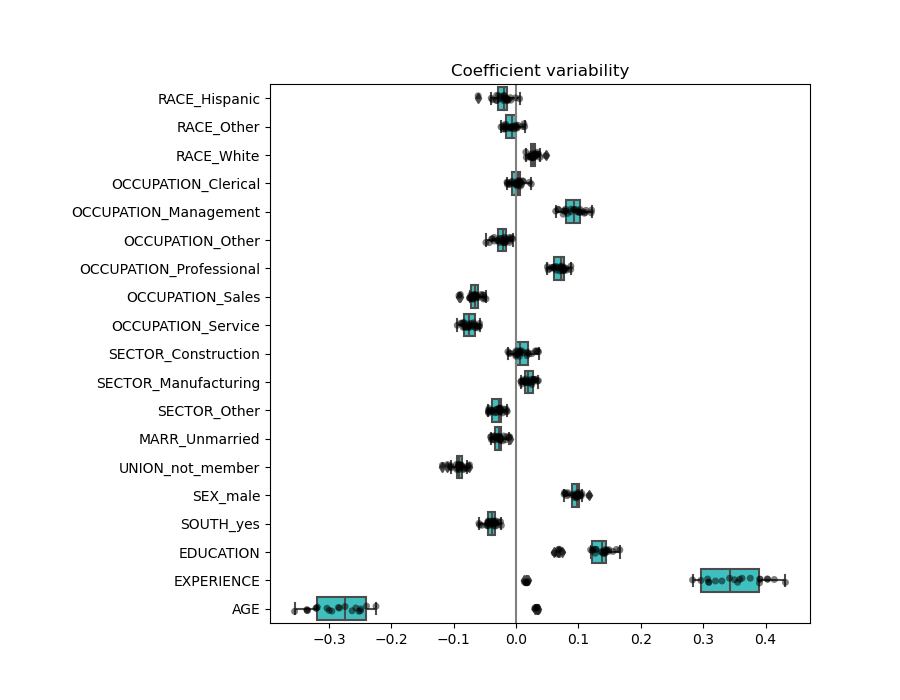
El resultado es bastante similar al caso no normalizado.
Modelos lineales con regularización¶
En la práctica del aprendizaje automático, la Regresión de Cresta se utiliza más a menudo con una regularización no despreciable.
Arriba, limitamos esta regularización a una cantidad muy pequeña. La regularización mejora el condicionamiento del problema y reduce la varianza de las estimaciones. RidgeCV aplica la validación cruzada para determinar qué valor del parámetro de regularización (alpha) es el más adecuado para la predicción.
from sklearn.linear_model import RidgeCV
model = make_pipeline(
preprocessor,
TransformedTargetRegressor(
regressor=RidgeCV(alphas=np.logspace(-10, 10, 21)),
func=np.log10,
inverse_func=sp.special.exp10
)
)
_ = model.fit(X_train, y_train)
Primero comprobamos qué valor de \(\alpha\) ha sido seleccionado.
model[-1].regressor_.alpha_
Out:
10.0
Luego comprobamos la calidad de las predicciones.
y_pred = model.predict(X_train)
mae = median_absolute_error(y_train, y_pred)
string_score = f'MAE on training set: {mae:.2f} $/hour'
y_pred = model.predict(X_test)
mae = median_absolute_error(y_test, y_pred)
string_score += f'\nMAE on testing set: {mae:.2f} $/hour'
fig, ax = plt.subplots(figsize=(6, 6))
plt.scatter(y_test, y_pred)
ax.plot([0, 1], [0, 1], transform=ax.transAxes, ls="--", c="red")
plt.text(3, 20, string_score)
plt.title('Ridge model, regularization, normalized variables')
plt.ylabel('Model predictions')
plt.xlabel('Truths')
plt.xlim([0, 27])
_ = plt.ylim([0, 27])
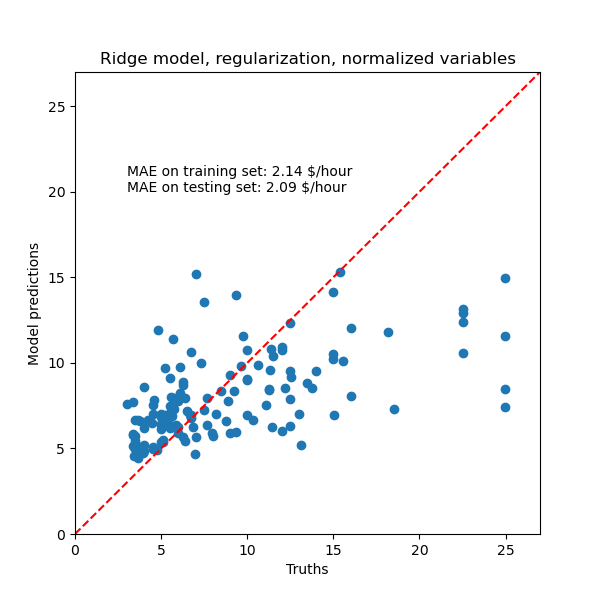
La capacidad de reproducir los datos del modelo regularizado es similar a la del modelo no regularizado.
coefs = pd.DataFrame(
model.named_steps['transformedtargetregressor'].regressor_.coef_,
columns=['Coefficients'], index=feature_names
)
coefs.plot(kind='barh', figsize=(9, 7))
plt.title('Ridge model, regularization, normalized variables')
plt.axvline(x=0, color='.5')
plt.subplots_adjust(left=.3)
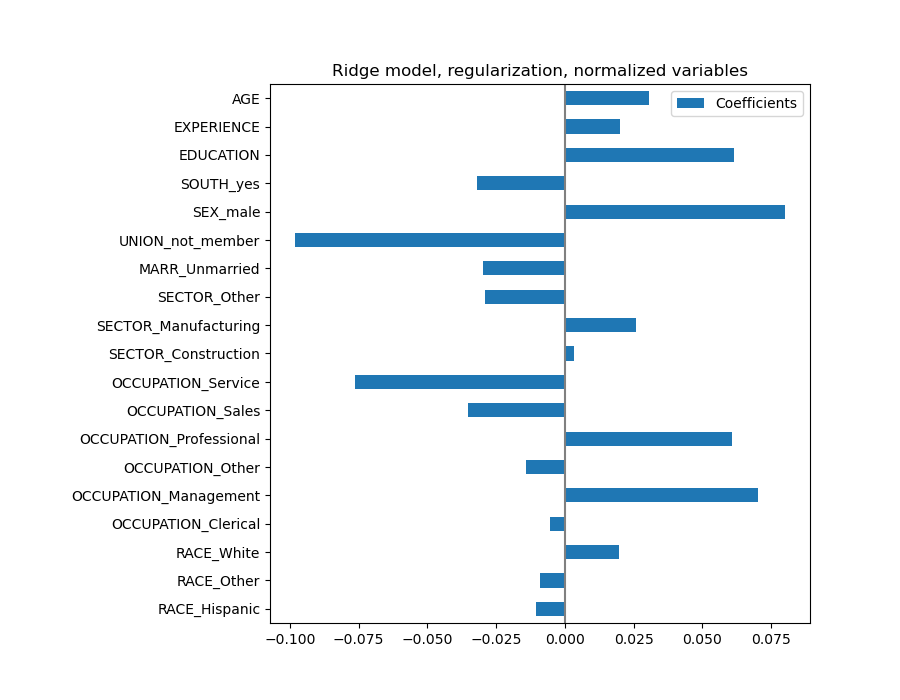
Los coeficientes son significativamente diferentes. Los coeficientes de AGE y EXPERIENCE son positivos, pero ahora tienen menos influencia en la predicción.
La regularización reduce la influencia de las variables correlacionadas en el modelo porque la ponderación se comparte entre las dos variables predictivas, por lo que ninguna de las dos por sí sola tendría ponderaciones fuertes.
Por otra parte, las ponderaciones obtenidas con la regularización son más estables (ver la sección del Manual de Usuario Regresión de cresta y clasificación). Esta mayor estabilidad es visible en el gráfico, obtenido a partir de las perturbaciones de los datos, en una validación cruzada. Este gráfico puede compararse con el anterior.
cv_model = cross_validate(
model, X, y, cv=RepeatedKFold(n_splits=5, n_repeats=5),
return_estimator=True, n_jobs=-1
)
coefs = pd.DataFrame(
[est.named_steps['transformedtargetregressor'].regressor_.coef_ *
X_train_preprocessed.std(axis=0)
for est in cv_model['estimator']],
columns=feature_names
)
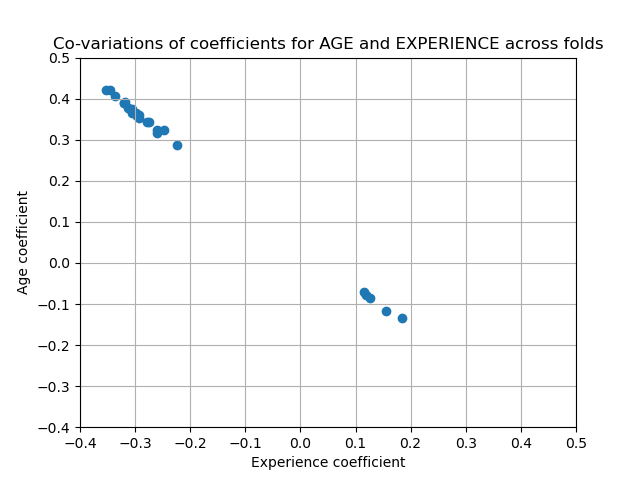
plt.ylabel('Age coefficient')
plt.xlabel('Experience coefficient')
plt.grid(True)
plt.xlim(-0.4, 0.5)
plt.ylim(-0.4, 0.5)
plt.scatter(coefs["AGE"], coefs["EXPERIENCE"])
_ = plt.title('Co-variations of coefficients for AGE and EXPERIENCE '
'across folds')
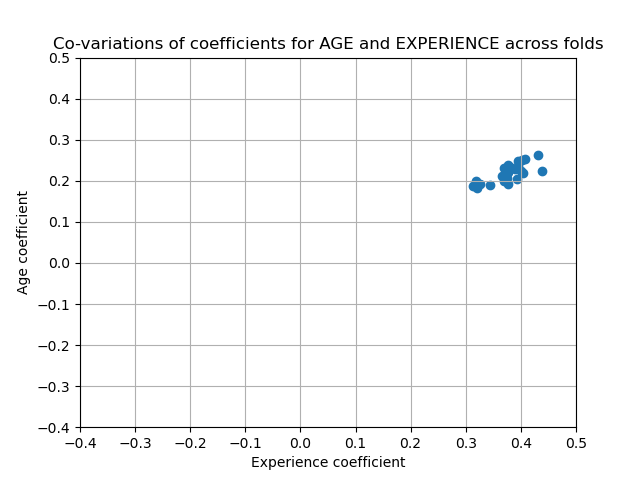
Modelos lineales con coeficientes dispersos¶
Otra posibilidad para tener en cuenta sobre las variables correlacionadas en el conjunto de datos, es estimar coeficientes dispersos. En cierto modo, ya lo hicimos manualmente cuando eliminamos la columna AGE en la estimación de Cresta anterior.
Los modelos Lasso (ver la sección del Manual de Usuario Lasso) estiman coeficientes dispersos. LassoCV aplica la validación cruzada para determinar qué valor del parámetro de regularización (alpha) es el más adecuado para la estimación del modelo.
from sklearn.linear_model import LassoCV
model = make_pipeline(
preprocessor,
TransformedTargetRegressor(
regressor=LassoCV(alphas=np.logspace(-10, 10, 21), max_iter=100000),
func=np.log10,
inverse_func=sp.special.exp10
)
)
_ = model.fit(X_train, y_train)
Primero verificamos qué valor de \(\alpha\) ha sido seleccionado.
model[-1].regressor_.alpha_
Out:
0.001
Luego comprobamos la calidad de las predicciones.
y_pred = model.predict(X_train)
mae = median_absolute_error(y_train, y_pred)
string_score = f'MAE on training set: {mae:.2f} $/hour'
y_pred = model.predict(X_test)
mae = median_absolute_error(y_test, y_pred)
string_score += f'\nMAE on testing set: {mae:.2f} $/hour'
fig, ax = plt.subplots(figsize=(6, 6))
plt.scatter(y_test, y_pred)
ax.plot([0, 1], [0, 1], transform=ax.transAxes, ls="--", c="red")
plt.text(3, 20, string_score)
plt.title('Lasso model, regularization, normalized variables')
plt.ylabel('Model predictions')
plt.xlabel('Truths')
plt.xlim([0, 27])
_ = plt.ylim([0, 27])
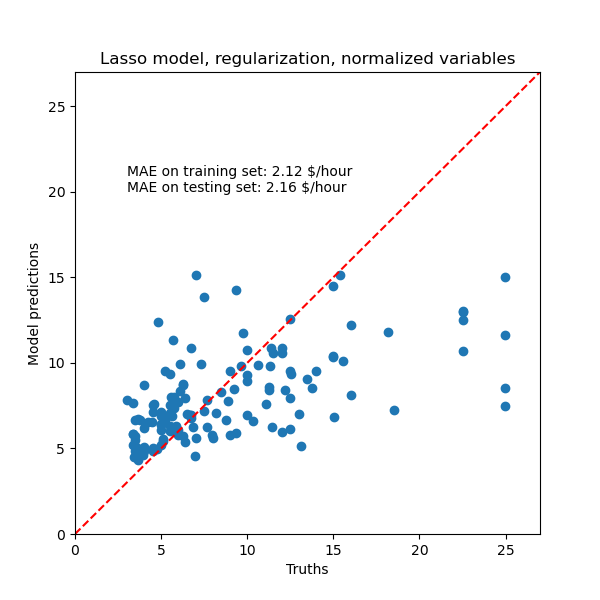
Para nuestro conjunto de datos, de nuevo el modelo no es muy predictivo.
coefs = pd.DataFrame(
model.named_steps['transformedtargetregressor'].regressor_.coef_,
columns=['Coefficients'], index=feature_names
)
coefs.plot(kind='barh', figsize=(9, 7))
plt.title('Lasso model, regularization, normalized variables')
plt.axvline(x=0, color='.5')
plt.subplots_adjust(left=.3)
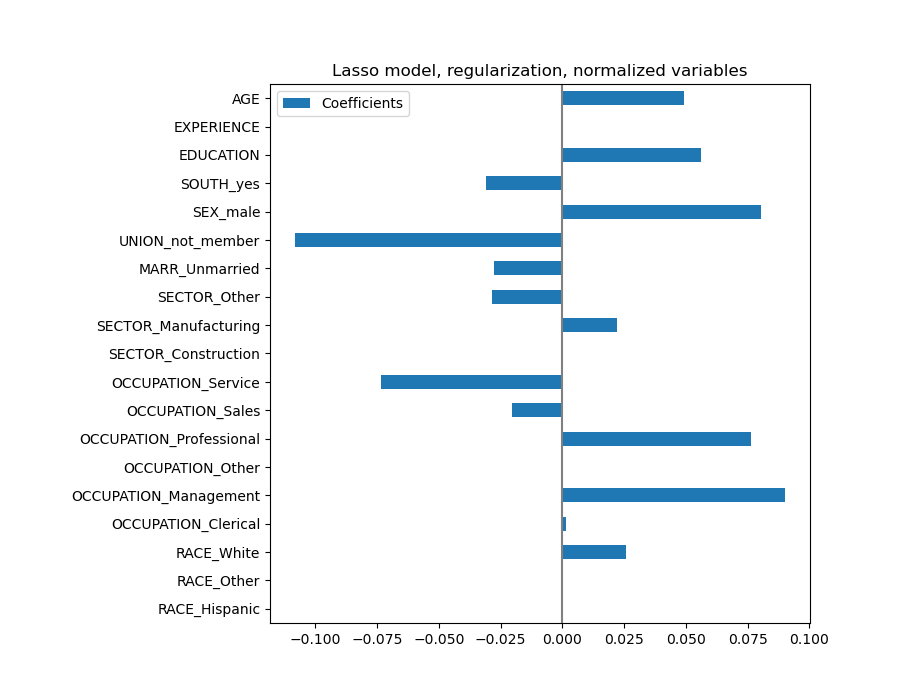
Un modelo Lasso identifica la correlación entre AGE y EXPERIENCE y suprime uno de ellas en aras de la predicción.
Es importante tener en cuenta que los coeficientes que se han eliminado aún pueden estar relacionados con el resultado por sí mismos: el modelo decidió suprimirlos porque aportan poca o ninguna información adicional sobre las otras características. Además, esta selección es inestable para las características correlacionadas, y debe interpretarse con precaución.
Lecciones aprendidas¶
Los coeficientes deben escalarse a la misma unidad de medida para recuperar la importancia de las características. Una aproximación útil es escalarlos con la desviación estándar de la característica.
Los coeficientes de los modelos lineales multivariantes representan la dependencia entre una característica determinada y el objetivo, condicionada a las demás características.
Las características correlacionadas inducen inestabilidades en los coeficientes de los modelos lineales y sus efectos no se pueden separar bien.
Los distintos modelos lineales responden de manera diferente a la correlación de las característica y los coeficientes podrían variar significativamente entre sí.
La inspección de los coeficientes en los pliegues de un bucle de validación cruzada da una idea de su estabilidad.
Tiempo total de ejecución del script: (0 minutos 17.976 segundos)
