Aprendizaje escalable con aproximación del núcleo polinomial

Este ejemplo ilustra el uso de PolynomialCountSketch para generar eficientemente aproximaciones de espacio en el núcleo polinomial. Esto se utiliza para entrenar clasificadores lineales que aproximan la precisión de los kernelizados.

Utilizamos el conjunto de datos Covtype [2], tratando de reproducir los experimentos del documento original de Tensor Sketch [1], es decir, el algoritmo implementado por PolynomialCountSketch.

Primero, calculamos la precisión de un clasificador lineal en las características originales. Luego, entrenamos clasificadores lineales en diferentes números de características (n_components) generados por PolynomialCountSketch, aproximar la precisión de un clasificador kernelizado de una manera escalable.

print(__doc__)

# Author: Daniel Lopez-Sanchez <lope@usal.es>
# License: BSD 3 clause
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_covtype
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler, Normalizer
from sklearn.svm import LinearSVC
from sklearn.kernel_approximation import PolynomialCountSketch
from sklearn.pipeline import Pipeline, make_pipeline
import time

Carga el conjunto de datos Covtype, que contiene 581.012 muestras con 54 características cada una, distribuidas entre 6 clases. El objetivo de este conjunto de datos es predecir el tipo de cubierta forestal únicamente a partir de variables cartográficas (sin datos de teledetección). Después de cargarlo, lo transformamos en un problema de clasificación binaria para que coincida con la versión del conjunto de datos en la página web de LIBSVM [2], que fue la que se utilizó en [1].

X, y = fetch_covtype(return_X_y=True)

y[y != 2] = 0
y[y == 2] = 1  # We will try to separate class 2 from the other 6 classes.

Aquí seleccionamos 5.000 muestras para entrenamiento y 10.000 para pruebas. Para reproducir realmente los resultados en el papel original del dibujo del sensor, selecciona 100.000 para entrenamiento.

X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=5_000,
                                                    test_size=10_000,
                                                    random_state=42)

Ahora escalamos las características al rango [0, 1] para que coincidan con el formato del conjunto de datos en la página web de LIBSVM, y luego las normalizamos a longitudes unitarias como se hizo en el documento original de Tensor Sketch [1].

mm = make_pipeline(MinMaxScaler(), Normalizer())
X_train = mm.fit_transform(X_train)
X_test = mm.transform(X_test)

Como línea de base, entrenar una SVM lineal sobre las características originales e imprimir la exactitud. También medimos y almacenamos exactitudes y tiempos de entrenamiento para tramitar estos últimos.

results = {}

lsvm = LinearSVC()
start = time.time()
lsvm.fit(X_train, y_train)
lsvm_time = time.time() - start
lsvm_score = 100 * lsvm.score(X_test, y_test)

results["LSVM"] = {"time": lsvm_time, "score": lsvm_score}
print(f"Linear SVM score on raw features: {lsvm_score:.2f}%")

Out:

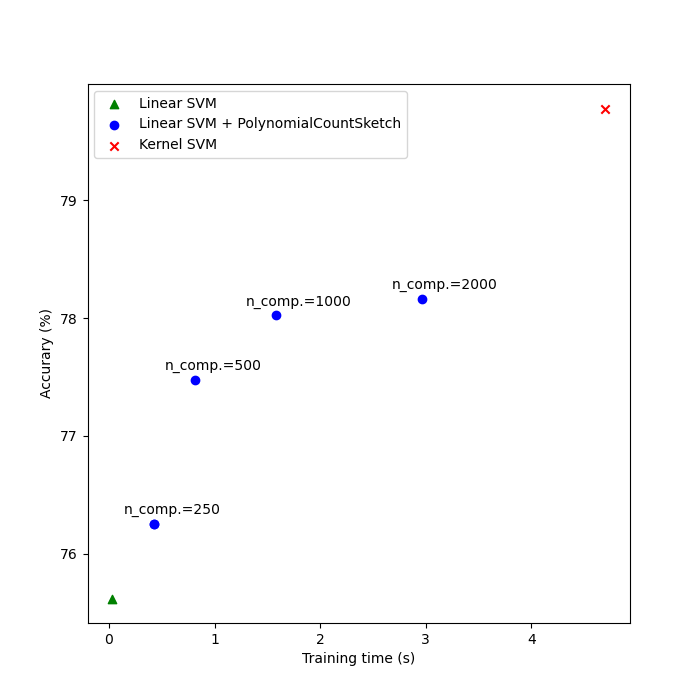
Linear SVM score on raw features: 75.62%

A continuación, entrenamos SVMs lineales en las características generadas por PolynomialCountSketch con diferentes valores para n_components, mostrando que estas aproximaciones de características del núcleo mejoran la precisión de la clasificación lineal. En los escenarios típicos de aplicación, n_components debe ser mayor que el número de características en la representación de entrada para lograr una mejora con respecto a la clasificación lineal. Como regla general, la puntuación óptima de la evaluación/coste del tiempo de ejecución suele alcanzarse en torno a n_components = 10 * n_features, aunque esto puede depender del conjunto de datos específico que se maneje. Ten en cuenta que, dado que las muestras originales tienen 54 características, el mapa de características explícito del núcleo polinómico de grado cuatro tendría aproximadamente 8,5 millones de características (exactamente, 54^4). Gracias a PolynomialCountSketch, podemos condensar la mayor parte de la información discriminativa de ese espacio de características en una representación mucho más compacta. Repetimos el experimento 5 veces para compensar la naturaleza estocástica de PolynomialCountSketch.

n_runs = 3
for n_components in [250, 500, 1000, 2000]:

    ps_lsvm_time = 0
    ps_lsvm_score = 0
    for _ in range(n_runs):

        pipeline = Pipeline(steps=[("kernel_approximator",
                                    PolynomialCountSketch(
                                        n_components=n_components,
                                        degree=4)),
                                   ("linear_classifier", LinearSVC())])

        start = time.time()
        pipeline.fit(X_train, y_train)
        ps_lsvm_time += time.time() - start
        ps_lsvm_score += 100 * pipeline.score(X_test, y_test)

    ps_lsvm_time /= n_runs
    ps_lsvm_score /= n_runs

    results[f"LSVM + PS({n_components})"] = {
        "time": ps_lsvm_time, "score": ps_lsvm_score
    }
    print(f"Linear SVM score on {n_components} PolynomialCountSketch " +
          f"features: {ps_lsvm_score:.2f}%")

Out:

Linear SVM score on 250 PolynomialCountSketch features: 76.26%
Linear SVM score on 500 PolynomialCountSketch features: 77.48%
Linear SVM score on 1000 PolynomialCountSketch features: 78.02%
Linear SVM score on 2000 PolynomialCountSketch features: 78.17%

Entrena un SVM kernelizado para ver qué tan bien PolynomialCountSketch se aproxima al rendimiento del núcleo. Esto, por supuesto, puede llevar algún tiempo, ya que la clase SVM tiene una escalabilidad relativamente pobre. Esta es la razón por la que los aproximadores del núcleo son tan útiles:

from sklearn.svm import SVC

ksvm = SVC(C=500., kernel="poly", degree=4, coef0=0, gamma=1.)

start = time.time()
ksvm.fit(X_train, y_train)
ksvm_time = time.time() - start
ksvm_score = 100 * ksvm.score(X_test, y_test)

results["KSVM"] = {"time": ksvm_time, "score": ksvm_score}
print(f"Kernel-SVM score on raw featrues: {ksvm_score:.2f}%")

Out:

Kernel-SVM score on raw featrues: 79.78%

Por último, traza los resultados de los diferentes métodos frente a sus tiempos de entrenamiento. Como podemos ver, la SVM kernelizada consigue una mayor precisión, pero su tiempo de entrenamiento es mucho mayor y, lo que es más importante, crecerá mucho más rápido si el número de muestras de entrenamiento aumenta.

N_COMPONENTS = [250, 500, 1000, 2000]

fig, ax = plt.subplots(figsize=(7, 7))
ax.scatter([results["LSVM"]["time"], ], [results["LSVM"]["score"], ],
           label="Linear SVM", c="green", marker="^")

ax.scatter([results["LSVM + PS(250)"]["time"], ],
           [results["LSVM + PS(250)"]["score"], ],
           label="Linear SVM + PolynomialCountSketch", c="blue")
for n_components in N_COMPONENTS:
    ax.scatter([results[f"LSVM + PS({n_components})"]["time"], ],
               [results[f"LSVM + PS({n_components})"]["score"], ],
               c="blue")
    ax.annotate(f"n_comp.={n_components}",
                (results[f"LSVM + PS({n_components})"]["time"],
                 results[f"LSVM + PS({n_components})"]["score"]),
                xytext=(-30, 10), textcoords="offset pixels")

ax.scatter([results["KSVM"]["time"], ], [results["KSVM"]["score"], ],
           label="Kernel SVM", c="red", marker="x")

ax.set_xlabel("Training time (s)")
ax.set_ylabel("Accurary (%)")
ax.legend()
plt.show()

Referencias

[1] Pham, Ninh and Rasmus Pagh. «Fast and scalable polynomial kernels via explicit feature maps.» KDD “13 (2013). https://doi.org/10.1145/2487575.2487591

[2] LIBSVM binary datasets repository https://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/binary.html