Gráficos de Dependencia Parcial y de Expectativa Condicional Individual

Los gráficos de dependencia parcial muestran la dependencia entre la función objetivo 2 y un conjunto de características de interés, marginando sobre los valores de todas las demás características (las características del complemento). Debido a los límites de la percepción humana, el tamaño del conjunto de características de interés debe ser pequeño (normalmente, uno o dos), por lo que se suelen elegir entre las características más importantes.

De forma similar, un gráfico de expectativa condicional individual (ICE) 3 muestra la dependencia entre la función objetivo y una característica de interés. Sin embargo, a diferencia de los gráficos de dependencia parcial, que muestran el efecto promedio de las características de interés, los gráficos ICE visualizan la dependencia de la predicción de una característica para cada muestra por separado, con una línea por muestra. Sólo se admite una característica de interés para los gráficos ICE.

Este ejemplo muestra cómo obtener gráficos de dependencia parcial e ICE de un MLPRegressor y un HistGradientBoostingRegressor entrenados en el conjunto de datos de viviendas de California. El ejemplo está tomado de 1.

1

T. Hastie, R. Tibshirani and J. Friedman, «Elements of Statistical Learning Ed. 2», Springer, 2009.

2

En el caso de la clasificación, se puede considerar como la puntuación de regresión antes de la función de enlace.

3

Goldstein, A., Kapelner, A., Bleich, J., and Pitkin, E., Peeking Inside the Black Box: Visualizing Statistical Learning With Plots of Individual Conditional Expectation. (2015) Journal of Computational and Graphical Statistics, 24(1): 44-65 (https://arxiv.org/abs/1309.6392)

print(__doc__)

Preprocesamiento de los datos de las Viviendas de California

Objetivo central para evitar el sesgo inicial de la potenciación de gradiente: la potenciación de gradiente con el método “recursion” no tiene en cuenta el estimador inicial (aquí el objetivo promedio, por defecto).

import pandas as pd
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split

cal_housing = fetch_california_housing()
X = pd.DataFrame(cal_housing.data, columns=cal_housing.feature_names)
y = cal_housing.target

y -= y.mean()

X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.1, random_state=0
)

Dependencia parcial unidireccional con diferentes modelos

En esta sección, calcularemos la dependencia parcial unidereccional con dos modelos diferentes de aprendizaje automático: (i) un perceptrón multicapa y (ii) una potenciación del gradiente. Con estos dos modelos, ilustramos cómo calcular e interpretar tanto el gráfico de dependencia parcial (PDP) como la expectativa condicional individual (ICE).

Perceptrón multicapa

Vamos a ajustar un MLPRegressor y calcular gráficos de dependencia parcial de una sola variable.

from time import time
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import QuantileTransformer
from sklearn.neural_network import MLPRegressor

print("Training MLPRegressor...")
tic = time()
est = make_pipeline(QuantileTransformer(),
                    MLPRegressor(hidden_layer_sizes=(50, 50),
                                 learning_rate_init=0.01,
                                 early_stopping=True))
est.fit(X_train, y_train)
print(f"done in {time() - tic:.3f}s")
print(f"Test R2 score: {est.score(X_test, y_test):.2f}")

Out:

Training MLPRegressor...
done in 8.881s
Test R2 score: 0.80

Configuramos un pipeline para escalar las características numéricas de entrada y ajustamos el tamaño de la red neuronal y la tasa de aprendizaje para obtener un compromiso razonable entre el tiempo de entrenamiento y el rendimiento predictivo en un conjunto de pruebas.

Es importante destacar que este conjunto de datos tabulares tiene rangos dinámicos muy diferentes para sus características. Las redes neuronales tienden a ser muy sensibles a las características con escalas variables y olvidarse de preprocesar la característica numérica conduciría a un modelo muy pobre.

Sería posible obtener un rendimiento predictivo aún mayor con una red neuronal más grande, pero el entrenamiento también sería significativamente más costoso.

Ten en cuenta que es importante comprobar que el modelo es lo suficientemente preciso en un conjunto de pruebas antes de graficar la dependencia parcial, ya que de poco serviría explicar el impacto de una característica determinada en la función de predicción de un modelo deficiente.

Graficaremos la dependencia parcial, tanto individual (ICE) como promediada (PDP). Nos limitamos a sólo 50 curvas ICE para no saturar el gráfico.

import matplotlib.pyplot as plt
from sklearn.inspection import partial_dependence
from sklearn.inspection import plot_partial_dependence

print('Computing partial dependence plots...')
tic = time()
features = ['MedInc', 'AveOccup', 'HouseAge', 'AveRooms']
display = plot_partial_dependence(
       est, X_train, features, kind="both", subsample=50,
       n_jobs=3, grid_resolution=20, random_state=0
)
print(f"done in {time() - tic:.3f}s")
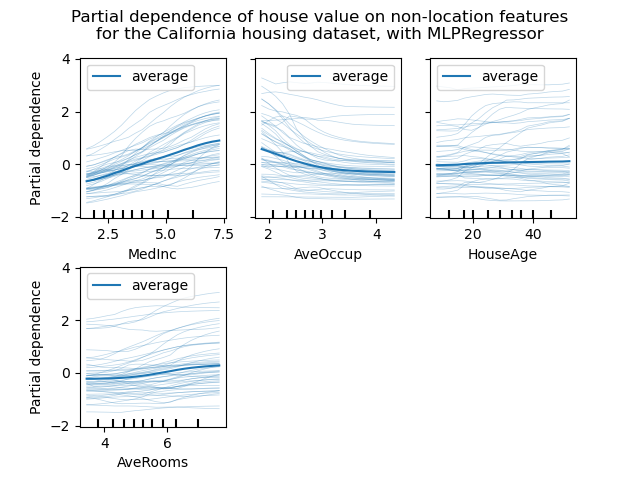
display.figure_.suptitle(
    'Partial dependence of house value on non-location features\n'
    'for the California housing dataset, with MLPRegressor'
)
display.figure_.subplots_adjust(hspace=0.3)

Out:

Computing partial dependence plots...
done in 3.048s

Potenciación del gradiente

Ahora vamos a ajustar un HistGradientBoostingRegressor y calcular la dependencia parcial de las mismas características.

from sklearn.experimental import enable_hist_gradient_boosting  # noqa
from sklearn.ensemble import HistGradientBoostingRegressor

print("Training HistGradientBoostingRegressor...")
tic = time()
est = HistGradientBoostingRegressor()
est.fit(X_train, y_train)
print(f"done in {time() - tic:.3f}s")
print(f"Test R2 score: {est.score(X_test, y_test):.2f}")

Out:

Training HistGradientBoostingRegressor...
done in 0.588s
Test R2 score: 0.85

En este caso, utilizamos los hiperparámetros predeterminados para el modelo de potenciación del gradiente sin ningún tipo de preprocesamiento, ya que los modelos basados en árboles son naturalmente robustos a las transformaciones monótonas de las características numéricas.

Observa que, en este conjunto de datos tabulares, las Máquinas de Potenciación del Gradiente son significativamente más rápidas de entrenar y más precisas que las redes neuronales. También es mucho más barato ajustar sus hiperparámetros (los valores predeterminados suelen funcionar bien, mientras que esto no suele ocurrir con las redes neuronales).

Graficaremos la dependencia parcial, tanto individual (ICE) como promediada (PDP). Nos limitamos a sólo 50 curvas ICE para no saturar el gráfico.

print('Computing partial dependence plots...')
tic = time()
display = plot_partial_dependence(
    est, X_train, features, kind="both", subsample=50,
    n_jobs=3, grid_resolution=20, random_state=0
)
print(f"done in {time() - tic:.3f}s")
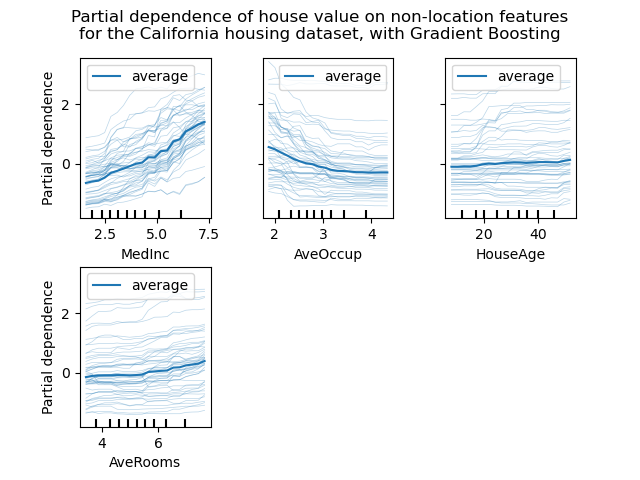
display.figure_.suptitle(
    'Partial dependence of house value on non-location features\n'
    'for the California housing dataset, with Gradient Boosting'
)
display.figure_.subplots_adjust(wspace=0.4, hspace=0.3)

Out:

Computing partial dependence plots...
done in 6.730s

Análisis de los gráficos

Podemos ver claramente en los PDP (línea azul gruesa) que la mediana del precio de la vivienda muestra una relación lineal con la mediana del ingreso (arriba a la izquierda) y que el precio de la vivienda baja cuando aumenta el promedio de ocupantes por hogar (arriba al centro). El gráfico de arriba a la derecha muestra que la edad de la vivienda en un distrito no tiene una gran influencia en el precio (mediana) de la vivienda; lo mismo ocurre con el promedio de habitaciones por hogar.

Las curvas ICE (líneas azul claro) complementan el análisis: podemos ver que hay algunas excepciones, en las que el precio de la vivienda permanece constante con la mediana del ingreso y los ocupantes promedio. Por otra parte, aunque la edad de la vivienda (arriba a la derecha) no tiene una gran influencia en la mediana del precio de la vivienda, parece que hay algunas excepciones en las que el precio de la vivienda aumenta cuando se encuentra entre los 15 y los 25 años. Se observan excepciones similares para el número promedio de habitaciones (abajo a la izquierda). Por lo tanto, los gráficos ICE muestran algún efecto individual que se atenúa al tomar los promedios.

En todos los gráficos, las marcas en el eje x representan los deciles de los valores de las características en los datos de entrenamiento.

También observamos que MLPRegressor tiene predicciones mucho más suaves que HistGradientBoostingRegressor.

Sin embargo, hay que tener en cuenta que estamos creando posibles muestras sintéticas sin sentido si las características están correlacionadas.

Gráficos de interacción 2D

Las PDP con dos características de interés nos permiten visualizar las interacciones entre ellas. Sin embargo, los ICE no se pueden trazar de forma sencilla y, por tanto, interpretar. Otra consideración está relacionada con el rendimiento para calcular los PDP. Con el algoritmo basado en el árbol, cuando sólo se solicitan los PDP, éstos pueden calcularse de forma eficiente utilizando el método 'recursion'.

features = ['AveOccup', 'HouseAge', ('AveOccup', 'HouseAge')]
print('Computing partial dependence plots...')
tic = time()
_, ax = plt.subplots(ncols=3, figsize=(9, 4))
display = plot_partial_dependence(
    est, X_train, features, kind='average', n_jobs=3, grid_resolution=20,
    ax=ax,
)
print(f"done in {time() - tic:.3f}s")
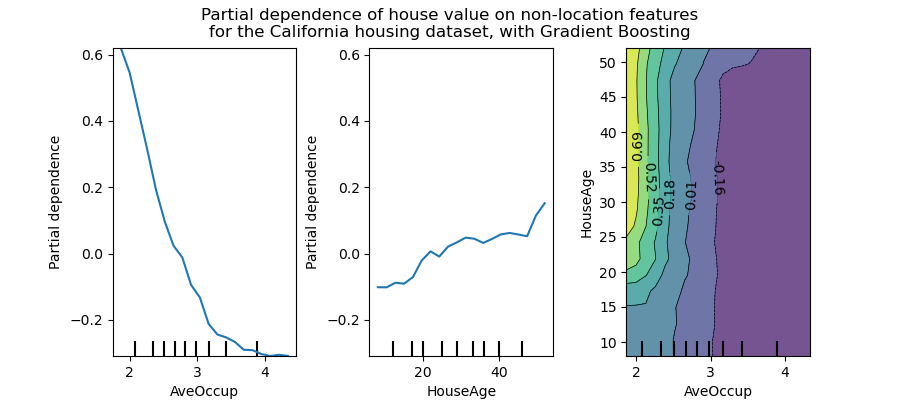
display.figure_.suptitle(
    'Partial dependence of house value on non-location features\n'
    'for the California housing dataset, with Gradient Boosting'
)
display.figure_.subplots_adjust(wspace=0.4, hspace=0.3)

Out:

Computing partial dependence plots...
done in 0.258s

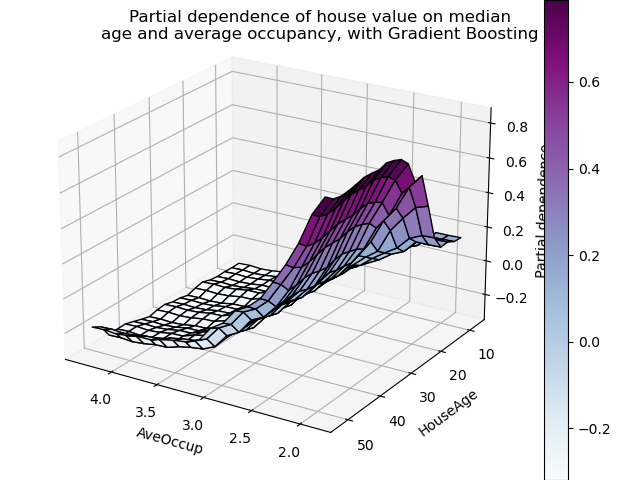
El gráfico de dependencia parcial bidireccional muestra la dependencia de la mediana del precio de la vivienda en los valores conjuntos de la edad de la vivienda y el promedio de ocupantes por hogar. Podemos ver claramente una interacción entre las dos características: para una ocupación promedio mayor a dos, el precio de la vivienda es casi independiente de la edad de la vivienda, mientras que para valores menores a dos hay una fuerte dependencia de la edad.

Gráficos de interacción 3D

Vamos a hacer el mismo gráfico de dependencia parcial para la interacción de 2 características, esta vez en 3 dimensiones.

import numpy as np
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()

features = ('AveOccup', 'HouseAge')
pdp = partial_dependence(
    est, X_train, features=features, kind='average', grid_resolution=20
)
XX, YY = np.meshgrid(pdp["values"][0], pdp["values"][1])
Z = pdp.average[0].T
ax = Axes3D(fig)
surf = ax.plot_surface(XX, YY, Z, rstride=1, cstride=1,
                       cmap=plt.cm.BuPu, edgecolor='k')
ax.set_xlabel(features[0])
ax.set_ylabel(features[1])
ax.set_zlabel('Partial dependence')
# pretty init view
ax.view_init(elev=22, azim=122)
plt.colorbar(surf)
plt.suptitle('Partial dependence of house value on median\n'
             'age and average occupancy, with Gradient Boosting')
plt.subplots_adjust(top=0.9)
plt.show()