Importancia de la Permutación vs la Importancia de las Características del Bosque Aleatorio (MDI)

En este ejemplo, compararemos la importancia de las características basadas en las impurezas de RandomForestClassifier con la importancia de la permutación en el conjunto de datos titanic utilizando permutation_importance. Mostraremos que la importancia de la característica basada en impurezas puede inflar la importancia de las características numéricas.

Además, la importancia de las características basadas en las impurezas de los bosques aleatorios se ve afectada por el hecho de que se calculan a partir de las estadísticas derivadas del conjunto de datos de entrenamiento: las importancias pueden ser altas incluso para las características que no son predictivas de la variable objetivo, siempre y cuando el modelo tenga la capacidad de utilizarlas para sobreajustar.

Este ejemplo muestra cómo utilizar las Importancias de Permutación como una alternativa que puede mitigar esas limitaciones.

Referencias:

[1] L. Breiman, «Random Forests», Machine Learning, 45(1), 5-32,

2001. https://doi.org/10.1023/A:1010933404324

print(__doc__)
import matplotlib.pyplot as plt
import numpy as np

from sklearn.datasets import fetch_openml
from sklearn.ensemble import RandomForestClassifier
from sklearn.impute import SimpleImputer
from sklearn.inspection import permutation_importance
from sklearn.compose import ColumnTransformer
from sklearn.model_selection import train_test_split
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import OneHotEncoder

Carga de Datos e Ingeniería de Características

Utilicemos pandas para cargar una copia del conjunto de datos del titanic. A continuación se muestra cómo aplicar el preprocesamiento por separado en características numéricas y categóricas.

Además, incluimos dos variables aleatorias que no están correlacionadas de ninguna manera con la variable objetivo (survived):

• random_num es una variable numérica de alta cardinalidad (tantos valores únicos como registros).

• random_cat es una variable categórica de baja cardinalidad (3 valores posibles).

X, y = fetch_openml("titanic", version=1, as_frame=True, return_X_y=True)
rng = np.random.RandomState(seed=42)
X['random_cat'] = rng.randint(3, size=X.shape[0])
X['random_num'] = rng.randn(X.shape[0])

categorical_columns = ['pclass', 'sex', 'embarked', 'random_cat']
numerical_columns = ['age', 'sibsp', 'parch', 'fare', 'random_num']

X = X[categorical_columns + numerical_columns]

X_train, X_test, y_train, y_test = train_test_split(
    X, y, stratify=y, random_state=42)

categorical_encoder = OneHotEncoder(handle_unknown='ignore')
numerical_pipe = Pipeline([
    ('imputer', SimpleImputer(strategy='mean'))
])

preprocessing = ColumnTransformer(
    [('cat', categorical_encoder, categorical_columns),
     ('num', numerical_pipe, numerical_columns)])

rf = Pipeline([
    ('preprocess', preprocessing),
    ('classifier', RandomForestClassifier(random_state=42))
])
rf.fit(X_train, y_train)

Out:

Pipeline(steps=[('preprocess',
                 ColumnTransformer(transformers=[('cat',
                                                  OneHotEncoder(handle_unknown='ignore'),
                                                  ['pclass', 'sex', 'embarked',
                                                   'random_cat']),
                                                 ('num',
                                                  Pipeline(steps=[('imputer',
                                                                   SimpleImputer())]),
                                                  ['age', 'sibsp', 'parch',
                                                   'fare', 'random_num'])])),
                ('classifier', RandomForestClassifier(random_state=42))])

Precisión del modelo

Antes de inspeccionar la importancia de las características, es fundamental comprobar que el rendimiento predictivo del modelo es lo suficientemente alto. De hecho, no tendría mucho interés inspeccionar las características importantes de un modelo no predictivo.

Aquí se puede observar que la precisión del entrenamiento es muy alta (el modelo de bosque tiene suficiente capacidad para memorizar completamente el conjunto de entrenamiento) pero todavía puede generalizar lo suficientemente bien al conjunto de prueba gracias al empaquetado incorporado de los bosques aleatorios.

Podría ser posible intercambiar algo de precisión en el conjunto de entrenamiento por una precisión ligeramente mejor en el conjunto de prueba limitando la capacidad de los árboles (por ejemplo, estableciendo min_samples_leaf=5 o min_samples_leaf=10) para limitar el sobreajuste sin introducir demasiado subajuste.

Sin embargo, vamos a mantener nuestro modelo de bosque aleatorio de alta capacidad por ahora para ilustrar algunas dificultades con la importancia de las características en las variables con muchos valores únicos.

print("RF train accuracy: %0.3f" % rf.score(X_train, y_train))
print("RF test accuracy: %0.3f" % rf.score(X_test, y_test))

Out:

RF train accuracy: 1.000
RF test accuracy: 0.817

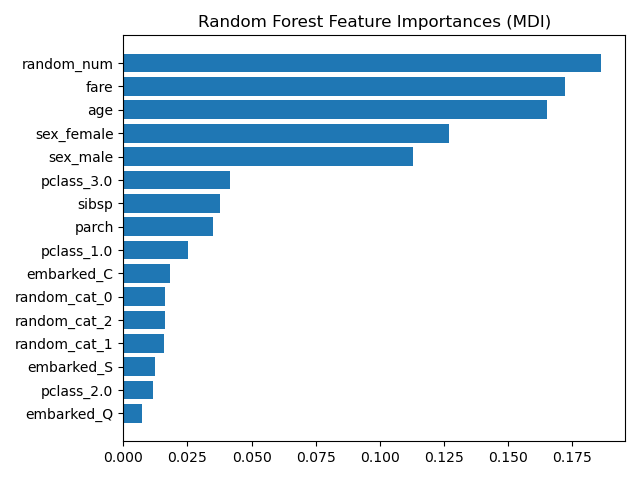
Importancia de la Característica del Árbol a partir de la Disminución Media de la Impureza (MDI)

La importancia de la característica basada en impurezas clasifica las características numéricas como las características más importantes. Como resultado, ¡la variable no predictiva random_num se clasifica como la más importante!

Este problema se debe a dos limitaciones de la importancia de las características basadas en las impurezas:

• las importancias basadas en las impurezas están sesgadas hacia las características de alta cardinalidad;

• las importancias basadas en las impurezas se calculan sobre las estadísticas del conjunto de entrenamiento y por tanto, no reflejan la capacidad de la característica de ser útil para hacer predicciones que se generalicen al conjunto de prueba (cuando el modelo tiene suficiente capacidad).

ohe = (rf.named_steps['preprocess']
         .named_transformers_['cat'])
feature_names = ohe.get_feature_names(input_features=categorical_columns)
feature_names = np.r_[feature_names, numerical_columns]

tree_feature_importances = (
    rf.named_steps['classifier'].feature_importances_)
sorted_idx = tree_feature_importances.argsort()

y_ticks = np.arange(0, len(feature_names))
fig, ax = plt.subplots()
ax.barh(y_ticks, tree_feature_importances[sorted_idx])
ax.set_yticklabels(feature_names[sorted_idx])
ax.set_yticks(y_ticks)
ax.set_title("Random Forest Feature Importances (MDI)")
fig.tight_layout()
plt.show()

Out:

/home/mapologo/Descargas/scikit-learn-0.24.X/examples/inspection/plot_permutation_importance.py:133: UserWarning: FixedFormatter should only be used together with FixedLocator
  ax.set_yticklabels(feature_names[sorted_idx])

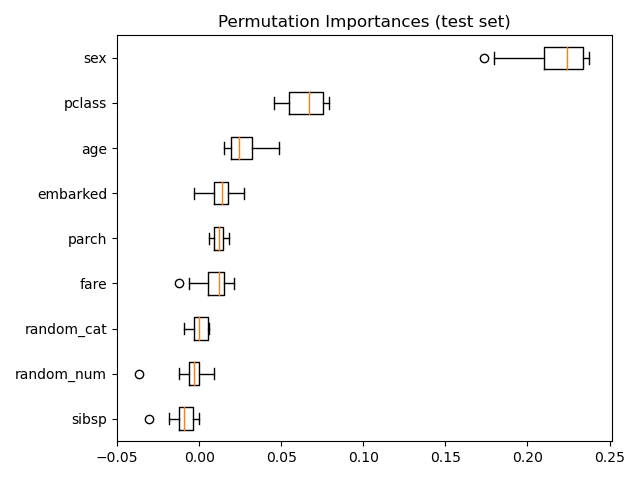
Como alternativa, las importancias de la permutación de rf se calculan en un conjunto de pruebas retenido. Esto muestra que la característica categórica de baja cardinalidad, «sex», es la característica más importante.

Observa también que ambas características aleatorias tienen importancias muy bajas (cercanas a 0), como era de esperar.

result = permutation_importance(rf, X_test, y_test, n_repeats=10,
                                random_state=42, n_jobs=2)
sorted_idx = result.importances_mean.argsort()

fig, ax = plt.subplots()
ax.boxplot(result.importances[sorted_idx].T,
           vert=False, labels=X_test.columns[sorted_idx])
ax.set_title("Permutation Importances (test set)")
fig.tight_layout()
plt.show()

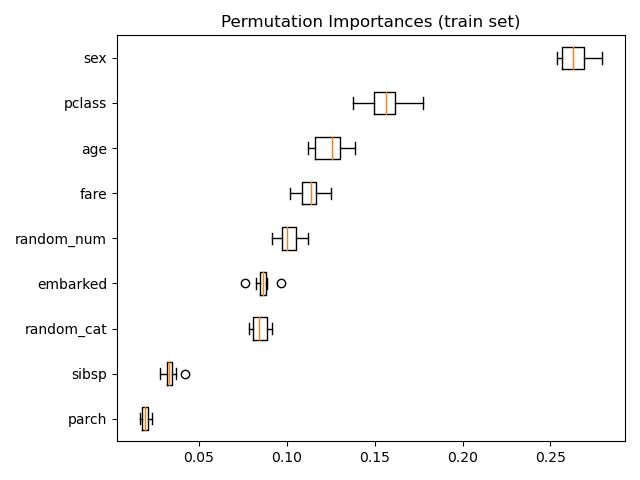
También es posible calcular las importancias de las permutaciones en el conjunto de entrenamiento. Esto revela que random_num obtiene una clasificación de importancias significativamente mayor que cuando se calcula en el conjunto de prueba. La diferencia entre esos dos gráficos es una confirmación de que el modelo de RF tiene suficiente capacidad para utilizar esa característica numérica aleatoria para sobreajustar. Puedes confirmarlo aún más volviendo a ejecutar este ejemplo con RF restringida con min_samples_leaf=10.

result = permutation_importance(rf, X_train, y_train, n_repeats=10,
                                random_state=42, n_jobs=2)
sorted_idx = result.importances_mean.argsort()

fig, ax = plt.subplots()
ax.boxplot(result.importances[sorted_idx].T,
           vert=False, labels=X_train.columns[sorted_idx])
ax.set_title("Permutation Importances (train set)")
fig.tight_layout()
plt.show()