Importancia de la Permutación con Características Multicolineales o Correlacionadas

En este ejemplo, calculamos la importancia de la permutación en el conjunto de datos de cáncer de mama de Wisconsin utilizando permutation_importance. El RandomForestClassifier puede obtener fácilmente alrededor del 97% de precisión en un conjunto de datos de prueba. Dado que este conjunto de datos contiene características multicolineales, la importancia de la permutación mostrará que ninguna de las características es importante. Un enfoque para manejar la multicolinealidad es realizar un agrupamiento jerárquico en las correlaciones de rangos de Spearman de las características, eligiendo un umbral y manteniendo una sola característica de cada grupo o conglomerado.

Nota

Ver también Importancia de la Permutación vs la Importancia de las Características del Bosque Aleatorio (MDI)

print(__doc__)
from collections import defaultdict

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import spearmanr
from scipy.cluster import hierarchy

from sklearn.datasets import load_breast_cancer
from sklearn.ensemble import RandomForestClassifier
from sklearn.inspection import permutation_importance
from sklearn.model_selection import train_test_split

Importancia de las Características Bosques Aleatorios en los Datos del Cáncer de Mama

Primero, entrenamos un bosque aleatorio en el conjunto de datos de cáncer de mama y evaluamos su precisión en un conjunto de pruebas:

data = load_breast_cancer()
X, y = data.data, data.target
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)

clf = RandomForestClassifier(n_estimators=100, random_state=42)
clf.fit(X_train, y_train)
print("Accuracy on test data: {:.2f}".format(clf.score(X_test, y_test)))

Out:

Accuracy on test data: 0.97

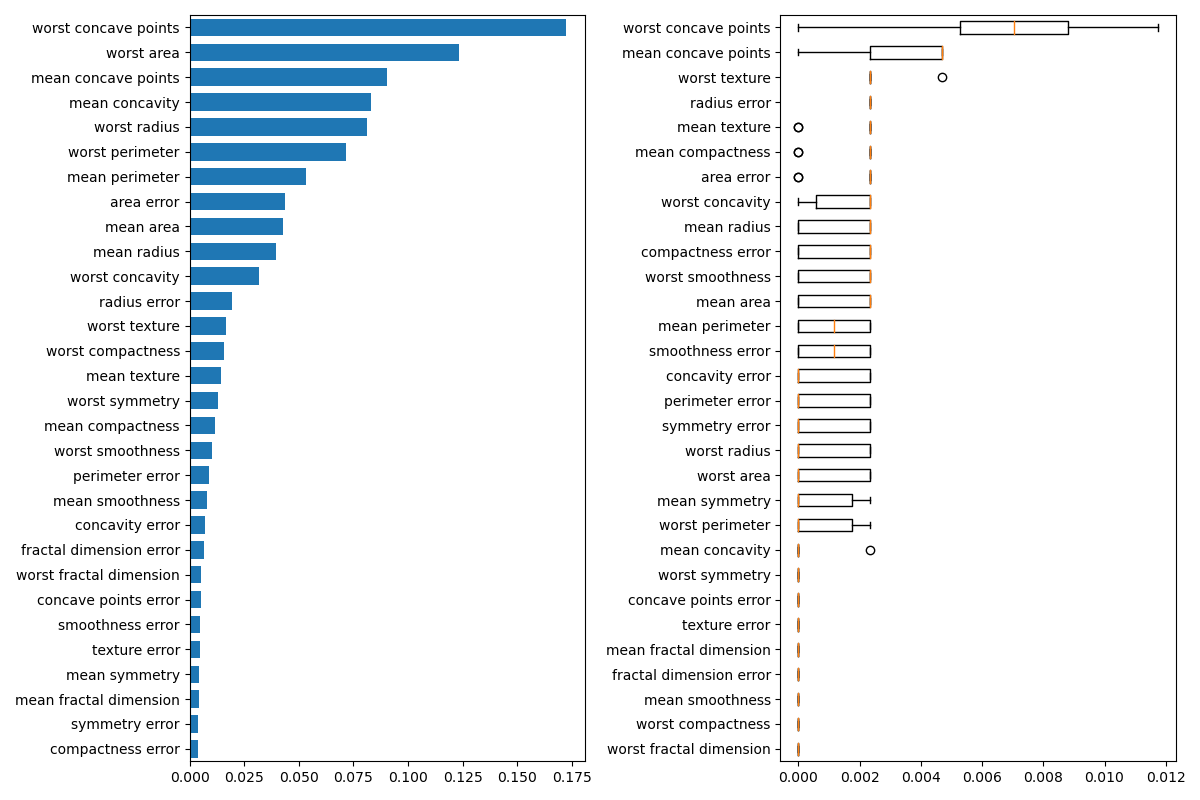
A continuación, trazamos la importancia de la característica basada en el árbol y la importancia de la permutación. El gráfico de la importancia de la permutación muestra que la permutación de una característica reduce la precisión en un máximo de 0.012, lo que sugiere que ninguna de las características es importante. Esto se contradice con la alta precisión de la prueba calculada anteriormente: alguna característica debe ser importante. La importancia de la permutación se calcula en el conjunto de entrenamiento para mostrar en qué medida el modelo depende de cada característica durante el entrenamiento.

result = permutation_importance(clf, X_train, y_train, n_repeats=10,
                                random_state=42)
perm_sorted_idx = result.importances_mean.argsort()

tree_importance_sorted_idx = np.argsort(clf.feature_importances_)
tree_indices = np.arange(0, len(clf.feature_importances_)) + 0.5

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 8))
ax1.barh(tree_indices,
         clf.feature_importances_[tree_importance_sorted_idx], height=0.7)
ax1.set_yticklabels(data.feature_names[tree_importance_sorted_idx])
ax1.set_yticks(tree_indices)
ax1.set_ylim((0, len(clf.feature_importances_)))
ax2.boxplot(result.importances[perm_sorted_idx].T, vert=False,
            labels=data.feature_names[perm_sorted_idx])
fig.tight_layout()
plt.show()

Out:

/home/mapologo/Descargas/scikit-learn-0.24.X/examples/inspection/plot_permutation_importance_multicollinear.py:63: UserWarning: FixedFormatter should only be used together with FixedLocator
  ax1.set_yticklabels(data.feature_names[tree_importance_sorted_idx])

Manejo de Características Multicolineales

Cuando las características son colineales, la permutación de una característica tendrá poco efecto en el rendimiento del modelo, ya que puede obtener la misma información de una característica correlacionada. Una forma de tratar las características multicolineales es realizar un agrupamiento jerárquico en las correlaciones de rangos de Spearman, eligiendo un umbral y manteniendo una única característica de cada grupo o conglomerado. En primer lugar, trazamos un mapa de calor de las características correlacionadas:

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 8))
corr = spearmanr(X).correlation
corr_linkage = hierarchy.ward(corr)
dendro = hierarchy.dendrogram(
    corr_linkage, labels=data.feature_names.tolist(), ax=ax1, leaf_rotation=90
)
dendro_idx = np.arange(0, len(dendro['ivl']))

ax2.imshow(corr[dendro['leaves'], :][:, dendro['leaves']])
ax2.set_xticks(dendro_idx)
ax2.set_yticks(dendro_idx)
ax2.set_xticklabels(dendro['ivl'], rotation='vertical')
ax2.set_yticklabels(dendro['ivl'])
fig.tight_layout()
plt.show()

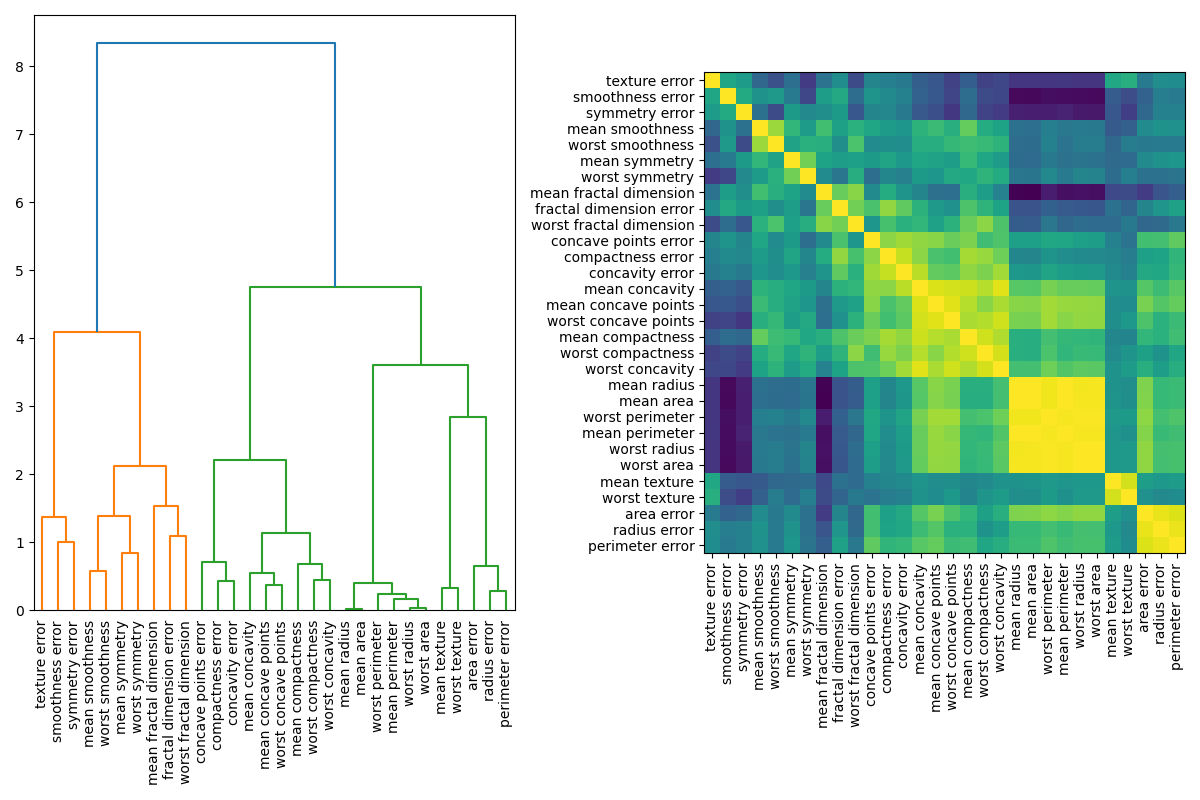
A continuación, elegimos manualmente un umbral mediante inspección visual del dendrograma para agrupar nuestras características en conglomerados y elegimos una característica de cada conglomerado para mantenerla, seleccionamos esas características de nuestro conjunto de datos y entrenamos un nuevo bosque aleatorio. La precisión de la prueba del nuevo bosque aleatorio no cambió mucho en comparación con el bosque aleatorio entrenado en el conjunto de datos completo.

cluster_ids = hierarchy.fcluster(corr_linkage, 1, criterion='distance')
cluster_id_to_feature_ids = defaultdict(list)
for idx, cluster_id in enumerate(cluster_ids):
    cluster_id_to_feature_ids[cluster_id].append(idx)
selected_features = [v[0] for v in cluster_id_to_feature_ids.values()]

X_train_sel = X_train[:, selected_features]
X_test_sel = X_test[:, selected_features]

clf_sel = RandomForestClassifier(n_estimators=100, random_state=42)
clf_sel.fit(X_train_sel, y_train)
print("Accuracy on test data with features removed: {:.2f}".format(
      clf_sel.score(X_test_sel, y_test)))

Out:

Accuracy on test data with features removed: 0.97