Nota
Haz clic en aquí para descargar el código completo del ejemplo o para ejecutar este ejemplo en tu navegador a través de Binder
Regresión de Tweedie en los reclamos de seguros¶
Este ejemplo ilustra el uso de la regresión de Poisson, Gamma y Tweedie en el conjunto de datos French Motor Third-Party Liability Claims, y está inspirado en un tutorial de R 1.
En este conjunto de datos, cada muestra corresponde a una póliza de seguro, es decir, a un contrato entre una compañía de seguros y un individuo (asegurado). Las características disponibles incluyen la edad del conductor, la edad del vehículo, la potencia del vehículo, etc.
Algunas definiciones: una reclamo es la petición que hace el asegurado a la aseguradora para que le compense un siniestro cubierto por el seguro. La cantidad de los reclamos es la cantidad de dinero que la aseguradora debe pagar. La exposición es la duración de la cobertura del seguro de una determinada póliza, en años.
En este caso, nuestro objetivo es predecir el valor esperado, es decir, la media, del importe total de los siniestros por unidad de exposición, también denominado prima pura.
Hay varias posibilidades para hacerlo, dos de las cuales son:
Modela el número de siniestros con una distribución de Poisson, y el importe medio de los siniestros, también conocido como gravedad, como una distribución Gamma y multiplica las predicciones de ambos para obtener el importe total de los siniestros.
Modela el importe total de los siniestros por exposición directamente, normalmente con una distribución de Tweedie de potencia \(p \Nen (1, 2)\).
En este ejemplo ilustraremos ambos enfoques. Comenzamos definiendo algunas funciones de ayuda para cargar los datos y visualizar los resultados.
- 1
A. Noll, R. Salzmann and M.V. Wuthrich, Case Study: French Motor Third-Party Liability Claims (November 8, 2018). doi:10.2139/ssrn.3164764
print(__doc__)
# Authors: Christian Lorentzen <lorentzen.ch@gmail.com>
# Roman Yurchak <rth.yurchak@gmail.com>
# Olivier Grisel <olivier.grisel@ensta.org>
# License: BSD 3 clause
from functools import partial
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.datasets import fetch_openml
from sklearn.compose import ColumnTransformer
from sklearn.linear_model import PoissonRegressor, GammaRegressor
from sklearn.linear_model import TweedieRegressor
from sklearn.metrics import mean_tweedie_deviance
from sklearn.model_selection import train_test_split
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import FunctionTransformer, OneHotEncoder
from sklearn.preprocessing import StandardScaler, KBinsDiscretizer
from sklearn.metrics import mean_absolute_error, mean_squared_error, auc
def load_mtpl2(n_samples=100000):
"""Fetch the French Motor Third-Party Liability Claims dataset.
Parameters
----------
n_samples: int, default=100000
number of samples to select (for faster run time). Full dataset has
678013 samples.
"""
# freMTPL2freq dataset from https://www.openml.org/d/41214
df_freq = fetch_openml(data_id=41214, as_frame=True)['data']
df_freq['IDpol'] = df_freq['IDpol'].astype(int)
df_freq.set_index('IDpol', inplace=True)
# freMTPL2sev dataset from https://www.openml.org/d/41215
df_sev = fetch_openml(data_id=41215, as_frame=True)['data']
# sum ClaimAmount over identical IDs
df_sev = df_sev.groupby('IDpol').sum()
df = df_freq.join(df_sev, how="left")
df["ClaimAmount"].fillna(0, inplace=True)
# unquote string fields
for column_name in df.columns[df.dtypes.values == object]:
df[column_name] = df[column_name].str.strip("'")
return df.iloc[:n_samples]
def plot_obs_pred(df, feature, weight, observed, predicted, y_label=None,
title=None, ax=None, fill_legend=False):
"""Plot observed and predicted - aggregated per feature level.
Parameters
----------
df : DataFrame
input data
feature: str
a column name of df for the feature to be plotted
weight : str
column name of df with the values of weights or exposure
observed : str
a column name of df with the observed target
predicted : DataFrame
a dataframe, with the same index as df, with the predicted target
fill_legend : bool, default=False
whether to show fill_between legend
"""
# aggregate observed and predicted variables by feature level
df_ = df.loc[:, [feature, weight]].copy()
df_["observed"] = df[observed] * df[weight]
df_["predicted"] = predicted * df[weight]
df_ = (
df_.groupby([feature])[[weight, "observed", "predicted"]]
.sum()
.assign(observed=lambda x: x["observed"] / x[weight])
.assign(predicted=lambda x: x["predicted"] / x[weight])
)
ax = df_.loc[:, ["observed", "predicted"]].plot(style=".", ax=ax)
y_max = df_.loc[:, ["observed", "predicted"]].values.max() * 0.8
p2 = ax.fill_between(
df_.index,
0,
y_max * df_[weight] / df_[weight].values.max(),
color="g",
alpha=0.1,
)
if fill_legend:
ax.legend([p2], ["{} distribution".format(feature)])
ax.set(
ylabel=y_label if y_label is not None else None,
title=title if title is not None else "Train: Observed vs Predicted",
)
def score_estimator(
estimator, X_train, X_test, df_train, df_test, target, weights,
tweedie_powers=None,
):
"""Evaluate an estimator on train and test sets with different metrics"""
metrics = [
("D² explained", None), # Use default scorer if it exists
("mean abs. error", mean_absolute_error),
("mean squared error", mean_squared_error),
]
if tweedie_powers:
metrics += [(
"mean Tweedie dev p={:.4f}".format(power),
partial(mean_tweedie_deviance, power=power)
) for power in tweedie_powers]
res = []
for subset_label, X, df in [
("train", X_train, df_train),
("test", X_test, df_test),
]:
y, _weights = df[target], df[weights]
for score_label, metric in metrics:
if isinstance(estimator, tuple) and len(estimator) == 2:
# Score the model consisting of the product of frequency and
# severity models.
est_freq, est_sev = estimator
y_pred = est_freq.predict(X) * est_sev.predict(X)
else:
y_pred = estimator.predict(X)
if metric is None:
if not hasattr(estimator, "score"):
continue
score = estimator.score(X, y, sample_weight=_weights)
else:
score = metric(y, y_pred, sample_weight=_weights)
res.append(
{"subset": subset_label, "metric": score_label, "score": score}
)
res = (
pd.DataFrame(res)
.set_index(["metric", "subset"])
.score.unstack(-1)
.round(4)
.loc[:, ['train', 'test']]
)
return res
Carga de conjuntos de datos, extracción de características básicas y definiciones de objetivos¶
Construimos el conjunto de datos freMTPL2 uniendo la tabla freMTPL2freq, que contiene el número de siniestros (ClaimNb), con la tabla freMTPL2sev, que contiene el importe de los siniestros (ClaimAmount) para los mismos identificadores de póliza (IDpol).
df = load_mtpl2(n_samples=60000)
# Note: filter out claims with zero amount, as the severity model
# requires strictly positive target values.
df.loc[(df["ClaimAmount"] == 0) & (df["ClaimNb"] >= 1), "ClaimNb"] = 0
# Correct for unreasonable observations (that might be data error)
# and a few exceptionally large claim amounts
df["ClaimNb"] = df["ClaimNb"].clip(upper=4)
df["Exposure"] = df["Exposure"].clip(upper=1)
df["ClaimAmount"] = df["ClaimAmount"].clip(upper=200000)
log_scale_transformer = make_pipeline(
FunctionTransformer(func=np.log),
StandardScaler()
)
column_trans = ColumnTransformer(
[
("binned_numeric", KBinsDiscretizer(n_bins=10),
["VehAge", "DrivAge"]),
("onehot_categorical", OneHotEncoder(),
["VehBrand", "VehPower", "VehGas", "Region", "Area"]),
("passthrough_numeric", "passthrough",
["BonusMalus"]),
("log_scaled_numeric", log_scale_transformer,
["Density"]),
],
remainder="drop",
)
X = column_trans.fit_transform(df)
# Insurances companies are interested in modeling the Pure Premium, that is
# the expected total claim amount per unit of exposure for each policyholder
# in their portfolio:
df["PurePremium"] = df["ClaimAmount"] / df["Exposure"]
# This can be indirectly approximated by a 2-step modeling: the product of the
# Frequency times the average claim amount per claim:
df["Frequency"] = df["ClaimNb"] / df["Exposure"]
df["AvgClaimAmount"] = df["ClaimAmount"] / np.fmax(df["ClaimNb"], 1)
with pd.option_context("display.max_columns", 15):
print(df[df.ClaimAmount > 0].head())
Out:
/home/mapologo/miniconda3/envs/sklearn/lib/python3.9/site-packages/scikit_learn-0.24.1-py3.9-linux-x86_64.egg/sklearn/datasets/_openml.py:849: UserWarning: Version 1 of dataset freMTPL2freq is inactive, meaning that issues have been found in the dataset. Try using a newer version from this URL: https://www.openml.org/data/v1/download/20649148/freMTPL2freq.arff
warn("Version {} of dataset {} is inactive, meaning that issues have "
/home/mapologo/miniconda3/envs/sklearn/lib/python3.9/site-packages/scikit_learn-0.24.1-py3.9-linux-x86_64.egg/sklearn/datasets/_openml.py:849: UserWarning: Version 1 of dataset freMTPL2sev is inactive, meaning that issues have been found in the dataset. Try using a newer version from this URL: https://www.openml.org/data/v1/download/20649149/freMTPL2sev.arff
warn("Version {} of dataset {} is inactive, meaning that issues have "
/home/mapologo/miniconda3/envs/sklearn/lib/python3.9/site-packages/scikit_learn-0.24.1-py3.9-linux-x86_64.egg/sklearn/preprocessing/_discretization.py:220: UserWarning: Bins whose width are too small (i.e., <= 1e-8) in feature 0 are removed. Consider decreasing the number of bins.
warnings.warn('Bins whose width are too small (i.e., <= '
ClaimNb Exposure Area VehPower VehAge DrivAge BonusMalus VehBrand \
IDpol
139 1.0 0.75 F 7.0 1.0 61.0 50.0 B12
190 1.0 0.14 B 12.0 5.0 50.0 60.0 B12
414 1.0 0.14 E 4.0 0.0 36.0 85.0 B12
424 2.0 0.62 F 10.0 0.0 51.0 100.0 B12
463 1.0 0.31 A 5.0 0.0 45.0 50.0 B12
VehGas Density Region ClaimAmount PurePremium Frequency \
IDpol
139 Regular 27000.0 R11 303.00 404.000000 1.333333
190 Diesel 56.0 R25 1981.84 14156.000000 7.142857
414 Regular 4792.0 R11 1456.55 10403.928571 7.142857
424 Regular 27000.0 R11 10834.00 17474.193548 3.225806
463 Regular 12.0 R73 3986.67 12860.225806 3.225806
AvgClaimAmount
IDpol
139 303.00
190 1981.84
414 1456.55
424 5417.00
463 3986.67
Modelo de frecuencia – Distribución de Poisson¶
El número de siniestros (ClaimNb) es un número entero positivo (incluido el 0). Por tanto, este objetivo puede modelizarse mediante una distribución de Poisson. Se supone entonces que es el número de eventos discretos que ocurren con una tasa constante en un intervalo de tiempo determinado (Exposición, en unidades de años). Aquí modelamos la frecuencia y = ClaimNb / Exposure, que sigue siendo una distribución de Poisson (a escala), y utilizamos Exposure como sample_weight.
df_train, df_test, X_train, X_test = train_test_split(df, X, random_state=0)
# The parameters of the model are estimated by minimizing the Poisson deviance
# on the training set via a quasi-Newton solver: l-BFGS. Some of the features
# are collinear, we use a weak penalization to avoid numerical issues.
glm_freq = PoissonRegressor(alpha=1e-3, max_iter=400)
glm_freq.fit(X_train, df_train["Frequency"],
sample_weight=df_train["Exposure"])
scores = score_estimator(
glm_freq,
X_train,
X_test,
df_train,
df_test,
target="Frequency",
weights="Exposure",
)
print("Evaluation of PoissonRegressor on target Frequency")
print(scores)
Out:
Evaluation of PoissonRegressor on target Frequency
subset train test
metric
D² explained 0.0590 0.0579
mean abs. error 0.1706 0.1661
mean squared error 0.3041 0.3043
Podemos comparar visualmente los valores observados y los previstos, agregados por la edad del conductor (DrivAge), la edad del vehículo (VehAge) y el bonus/malus del seguro (BonusMalus).
fig, ax = plt.subplots(ncols=2, nrows=2, figsize=(16, 8))
fig.subplots_adjust(hspace=0.3, wspace=0.2)
plot_obs_pred(
df=df_train,
feature="DrivAge",
weight="Exposure",
observed="Frequency",
predicted=glm_freq.predict(X_train),
y_label="Claim Frequency",
title="train data",
ax=ax[0, 0],
)
plot_obs_pred(
df=df_test,
feature="DrivAge",
weight="Exposure",
observed="Frequency",
predicted=glm_freq.predict(X_test),
y_label="Claim Frequency",
title="test data",
ax=ax[0, 1],
fill_legend=True
)
plot_obs_pred(
df=df_test,
feature="VehAge",
weight="Exposure",
observed="Frequency",
predicted=glm_freq.predict(X_test),
y_label="Claim Frequency",
title="test data",
ax=ax[1, 0],
fill_legend=True
)
plot_obs_pred(
df=df_test,
feature="BonusMalus",
weight="Exposure",
observed="Frequency",
predicted=glm_freq.predict(X_test),
y_label="Claim Frequency",
title="test data",
ax=ax[1, 1],
fill_legend=True
)
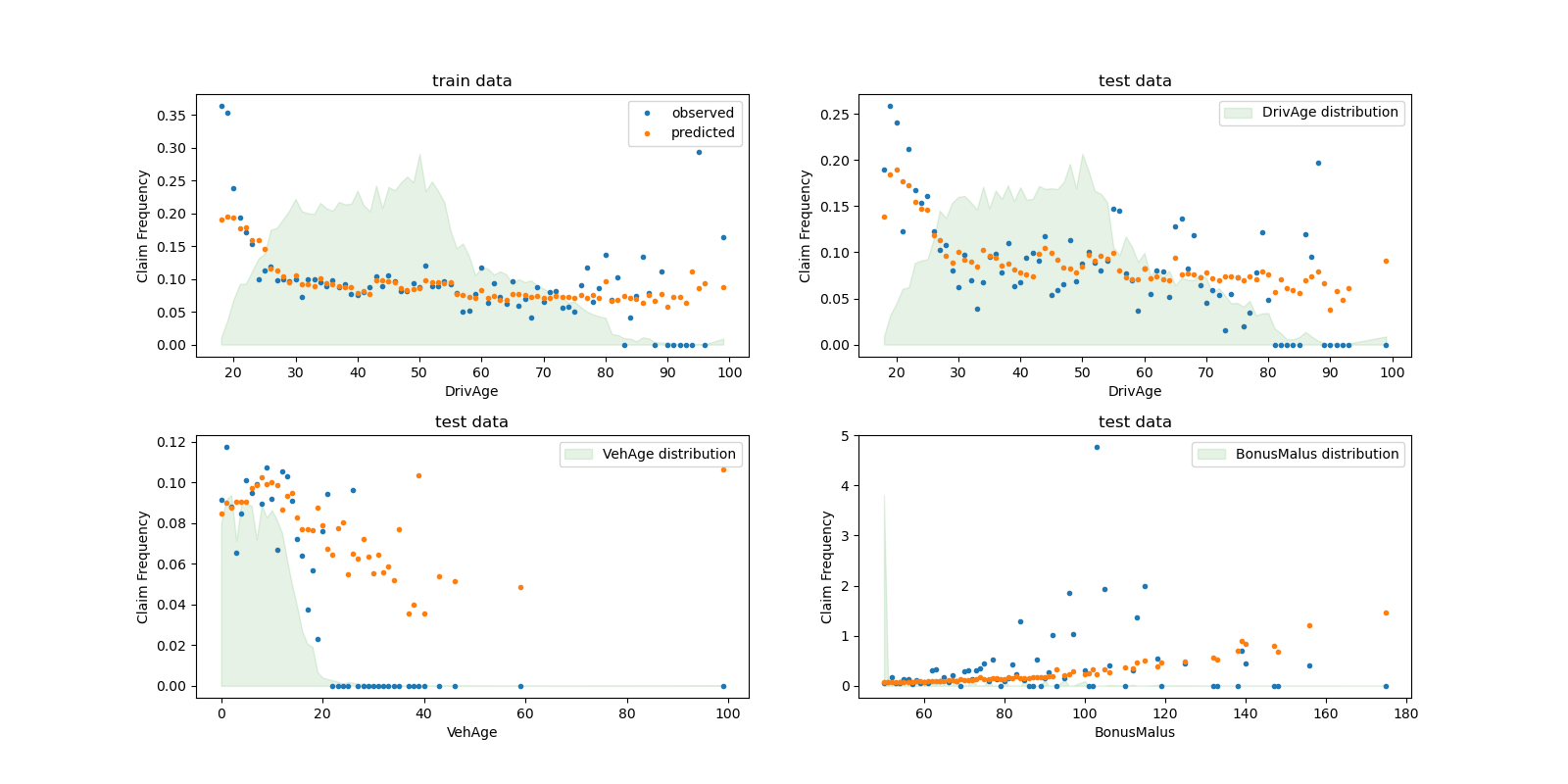
Según los datos observados, la frecuencia de los accidentes es mayor para los conductores menores de 30 años, y está positivamente correlacionada con la variable BonusMalus. Nuestro modelo es capaz de modelar correctamente este comportamiento.
Modelo de gravedad - Distribución gamma¶
Se puede demostrar empíricamente que el importe medio de los siniestros o la gravedad (AvgClaimAmount) sigue aproximadamente una distribución Gamma. Ajustamos un modelo GLM para la gravedad con las mismas características que el modelo de frecuencia.
Nota:
Filtramos
ClaimAmount == 0ya que la distribución Gamma tiene soporte en \((0, \infty)\), no en \([0, \infty)\).Utilizamos «ClaimNb» como
sample_weightpara tener en cuenta las pólizas que contienen más de un siniestro.
mask_train = df_train["ClaimAmount"] > 0
mask_test = df_test["ClaimAmount"] > 0
glm_sev = GammaRegressor(alpha=10., max_iter=10000)
glm_sev.fit(
X_train[mask_train.values],
df_train.loc[mask_train, "AvgClaimAmount"],
sample_weight=df_train.loc[mask_train, "ClaimNb"],
)
scores = score_estimator(
glm_sev,
X_train[mask_train.values],
X_test[mask_test.values],
df_train[mask_train],
df_test[mask_test],
target="AvgClaimAmount",
weights="ClaimNb",
)
print("Evaluation of GammaRegressor on target AvgClaimAmount")
print(scores)
Out:
Evaluation of GammaRegressor on target AvgClaimAmount
subset train test
metric
D² explained 4.300000e-03 -1.380000e-02
mean abs. error 1.699197e+03 2.027923e+03
mean squared error 4.548147e+07 6.094863e+07
En este caso, las puntuaciones de los datos de prueba exigen precaución, ya que son significativamente peores que las de los datos de entrenamiento, lo que indica un sobreajuste a pesar de la fuerte regularización.
Hay que tener en cuenta que el modelo resultante es el importe medio de los siniestros por póliza. Como tal, está condicionado a tener al menos un siniestro, y no puede utilizarse para predecir el importe medio de los siniestros por póliza en general.
print("Mean AvgClaim Amount per policy: %.2f "
% df_train["AvgClaimAmount"].mean())
print("Mean AvgClaim Amount | NbClaim > 0: %.2f"
% df_train["AvgClaimAmount"][df_train["AvgClaimAmount"] > 0].mean())
print("Predicted Mean AvgClaim Amount | NbClaim > 0: %.2f"
% glm_sev.predict(X_train).mean())
Out:
Mean AvgClaim Amount per policy: 97.89
Mean AvgClaim Amount | NbClaim > 0: 1899.60
Predicted Mean AvgClaim Amount | NbClaim > 0: 1884.40
Podemos comparar visualmente los valores observados y previstos, agregados para la edad del conductor (DrivAge).
fig, ax = plt.subplots(ncols=1, nrows=2, figsize=(16, 6))
plot_obs_pred(
df=df_train.loc[mask_train],
feature="DrivAge",
weight="Exposure",
observed="AvgClaimAmount",
predicted=glm_sev.predict(X_train[mask_train.values]),
y_label="Average Claim Severity",
title="train data",
ax=ax[0],
)
plot_obs_pred(
df=df_test.loc[mask_test],
feature="DrivAge",
weight="Exposure",
observed="AvgClaimAmount",
predicted=glm_sev.predict(X_test[mask_test.values]),
y_label="Average Claim Severity",
title="test data",
ax=ax[1],
fill_legend=True
)
plt.tight_layout()
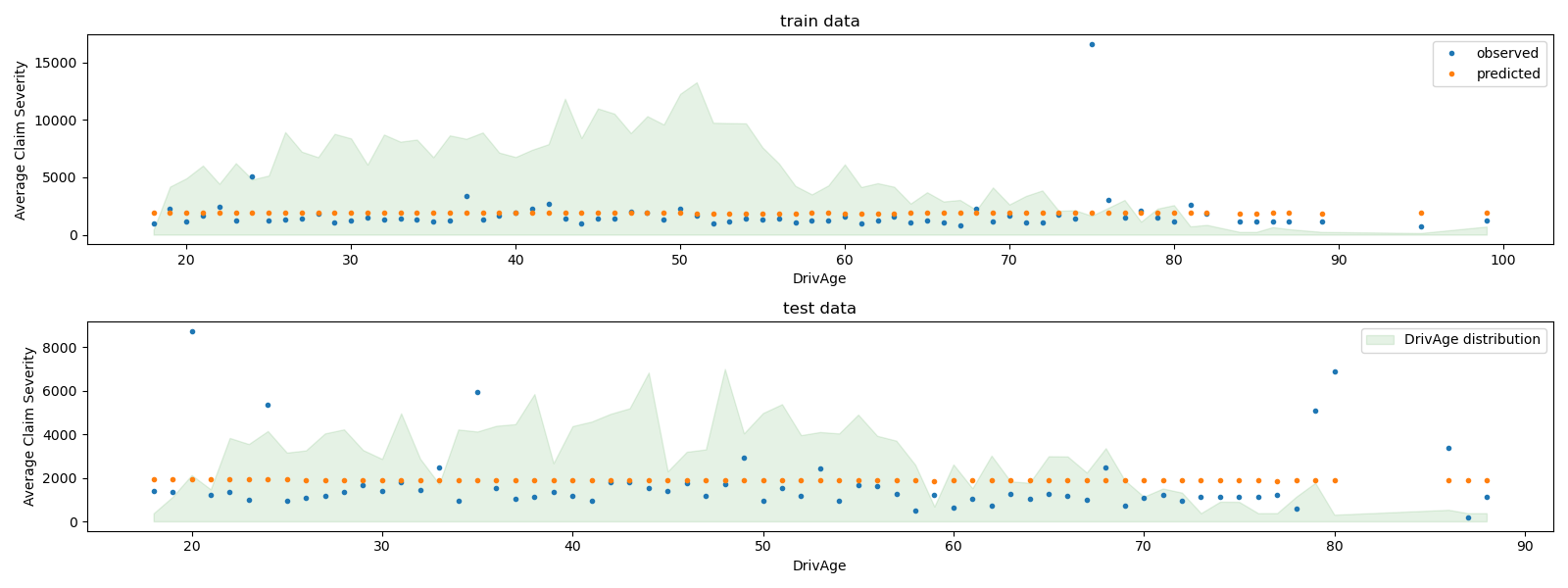
En general, la edad del conductor (DrivAge) tiene un impacto débil en la gravedad de los siniestros, tanto en los datos observados como en los previstos.
Modelización de la prima pura mediante un modelo de producto frente a un único TweedieRegressor¶
Como se ha mencionado en la introducción, el importe total de los siniestros por unidad de exposición puede modelarse como el producto de la predicción del modelo de frecuencia por la predicción del modelo de gravedad.
Como alternativa, se puede modelar directamente la pérdida total con un único modelo lineal generalizado de Poisson Gamma Compuesto (con una función de enlace logarítmica). Este modelo es un caso especial del MLG de Tweedie con un parámetro de «power» \(p \in (1, 2)\). En este caso, fijamos a priori el parámetro de power del modelo de Tweedie en un valor arbitrario (1.9) dentro del rango válido. Lo ideal sería seleccionar este valor a través de la búsqueda en cuadrícula minimizando el logaritmo de la verosimilitud negativa del modelo de Tweedie, pero desafortunadamente la implementación actual no permite esto (todavía).
Compararemos el rendimiento de ambos enfoques. Para cuantificar el rendimiento de ambos modelos, se puede calcular la desviación media de los datos de entrenamiento y de prueba suponiendo una distribución Poisson-Gamma compuesta del importe total de la reclamación. Esto equivale a una distribución de Tweedie con un parámetro de power entre 1 y 2.
La sklearn.metrics.mean_tweedie_deviance depende de un parámetro power. Como no conocemos el valor real del parámetro power, aquí calculamos las desviaciones medias para una parrilla de valores posibles, y comparamos los modelos uno al lado del otro, es decir, los comparamos con valores idénticos de power. Idealmente, esperamos que un modelo sea sistemáticamente mejor que el otro, independientemente de la power.
glm_pure_premium = TweedieRegressor(power=1.9, alpha=.1, max_iter=10000)
glm_pure_premium.fit(X_train, df_train["PurePremium"],
sample_weight=df_train["Exposure"])
tweedie_powers = [1.5, 1.7, 1.8, 1.9, 1.99, 1.999, 1.9999]
scores_product_model = score_estimator(
(glm_freq, glm_sev),
X_train,
X_test,
df_train,
df_test,
target="PurePremium",
weights="Exposure",
tweedie_powers=tweedie_powers,
)
scores_glm_pure_premium = score_estimator(
glm_pure_premium,
X_train,
X_test,
df_train,
df_test,
target="PurePremium",
weights="Exposure",
tweedie_powers=tweedie_powers
)
scores = pd.concat([scores_product_model, scores_glm_pure_premium],
axis=1, sort=True,
keys=('Product Model', 'TweedieRegressor'))
print("Evaluation of the Product Model and the Tweedie Regressor "
"on target PurePremium")
with pd.option_context('display.expand_frame_repr', False):
print(scores)
Out:
Evaluation of the Product Model and the Tweedie Regressor on target PurePremium
Product Model TweedieRegressor
subset train test train test
metric
D² explained NaN NaN 2.550000e-02 2.480000e-02
mean Tweedie dev p=1.5000 8.217800e+01 8.639750e+01 7.960780e+01 8.618780e+01
mean Tweedie dev p=1.7000 3.833700e+01 3.920270e+01 3.737390e+01 3.917480e+01
mean Tweedie dev p=1.8000 3.106890e+01 3.148660e+01 3.047890e+01 3.148140e+01
mean Tweedie dev p=1.9000 3.396240e+01 3.420550e+01 3.360060e+01 3.420830e+01
mean Tweedie dev p=1.9900 1.989243e+02 1.996416e+02 1.986911e+02 1.996462e+02
mean Tweedie dev p=1.9990 1.886429e+03 1.892748e+03 1.886206e+03 1.892753e+03
mean Tweedie dev p=1.9999 1.876452e+04 1.882692e+04 1.876430e+04 1.882692e+04
mean abs. error 3.246831e+02 3.469773e+02 3.202432e+02 3.397005e+02
mean squared error 1.469183e+08 3.325903e+07 1.469327e+08 3.325470e+07
En este ejemplo, ambos enfoques de modelización ofrecen métricas de rendimiento comparables. Por razones de implementación, el porcentaje de varianza explicada \(D^2\) no está disponible para el modelo de producto.
Además, podemos validar estos modelos comparando el importe total de siniestros observado y predicho en los subconjuntos de prueba y de entrenamiento. Vemos que, en promedio, ambos modelos tienden a subestimar la siniestralidad total (pero este comportamiento depende de la cantidad de regularización).
res = []
for subset_label, X, df in [
("train", X_train, df_train),
("test", X_test, df_test),
]:
exposure = df["Exposure"].values
res.append(
{
"subset": subset_label,
"observed": df["ClaimAmount"].values.sum(),
"predicted, frequency*severity model": np.sum(
exposure * glm_freq.predict(X) * glm_sev.predict(X)
),
"predicted, tweedie, power=%.2f"
% glm_pure_premium.power: np.sum(
exposure * glm_pure_premium.predict(X)),
}
)
print(pd.DataFrame(res).set_index("subset").T)
Out:
subset train test
observed 4.577616e+06 1.725665e+06
predicted, frequency*severity model 4.565330e+06 1.495512e+06
predicted, tweedie, power=1.90 4.451462e+06 1.431938e+06
Por último, podemos comparar los dos modelos utilizando un gráfico de los siniestros acumulados: para cada modelo, los asegurados se clasifican de más seguros a más arriesgados y la fracción de los siniestros totales acumulados observados se representa en el eje Y. Este Gráfico suele denominarse curva de Lorenz ordenada del modelo.
El coeficiente de Gini (basado en el área bajo la curva) puede utilizarse como métrica de selección de modelos para cuantificar la capacidad del modelo de clasificar a los asegurados. Hay que tener en cuenta que esta métrica no refleja la capacidad de los modelos para hacer predicciones precisas en términos de valor absoluto de los importes totales de los siniestros, sino sólo en términos de importes relativos como métrica de clasificación.
Ambos modelos son capaces de clasificar a los asegurados por su nivel de riesgo significativamente mejor que el azar, aunque también están lejos de ser perfectos debido a la dificultad natural del problema de predicción a partir de pocas características.
Observa que el índice de Gini sólo caracteriza el rendimiento de la clasificación del modelo, pero no su calibración: cualquier transformación monótona de las predicciones deja inalterado el índice de Gini del modelo.
Por último, cabe destacar que el modelo Gamma de Poisson compuesto que se ajusta directamente a la prima pura es operativamente más sencillo de desarrollar y mantener, ya que consiste en un único estimador de scikit-learn en lugar de un par de modelos, cada uno con su propio conjunto de hiperparámetros.
def lorenz_curve(y_true, y_pred, exposure):
y_true, y_pred = np.asarray(y_true), np.asarray(y_pred)
exposure = np.asarray(exposure)
# order samples by increasing predicted risk:
ranking = np.argsort(y_pred)
ranked_exposure = exposure[ranking]
ranked_pure_premium = y_true[ranking]
cumulated_claim_amount = np.cumsum(ranked_pure_premium * ranked_exposure)
cumulated_claim_amount /= cumulated_claim_amount[-1]
cumulated_samples = np.linspace(0, 1, len(cumulated_claim_amount))
return cumulated_samples, cumulated_claim_amount
fig, ax = plt.subplots(figsize=(8, 8))
y_pred_product = glm_freq.predict(X_test) * glm_sev.predict(X_test)
y_pred_total = glm_pure_premium.predict(X_test)
for label, y_pred in [("Frequency * Severity model", y_pred_product),
("Compound Poisson Gamma", y_pred_total)]:
ordered_samples, cum_claims = lorenz_curve(
df_test["PurePremium"], y_pred, df_test["Exposure"])
gini = 1 - 2 * auc(ordered_samples, cum_claims)
label += " (Gini index: {:.3f})".format(gini)
ax.plot(ordered_samples, cum_claims, linestyle="-", label=label)
# Oracle model: y_pred == y_test
ordered_samples, cum_claims = lorenz_curve(
df_test["PurePremium"], df_test["PurePremium"], df_test["Exposure"])
gini = 1 - 2 * auc(ordered_samples, cum_claims)
label = "Oracle (Gini index: {:.3f})".format(gini)
ax.plot(ordered_samples, cum_claims, linestyle="-.", color="gray",
label=label)
# Random baseline
ax.plot([0, 1], [0, 1], linestyle="--", color="black",
label="Random baseline")
ax.set(
title="Lorenz Curves",
xlabel=('Fraction of policyholders\n'
'(ordered by model from safest to riskiest)'),
ylabel='Fraction of total claim amount'
)
ax.legend(loc="upper left")
plt.plot()
Out:
[]
Tiempo total de ejecución del script: (0 minutos 33.168 segundos)
