Nota
Haz clic en aquí para descargar el código de ejemplo completo o para ejecutar este ejemplo en tu navegador a través de Binder
Regresión de Poisson y pérdida no normal¶
Este ejemplo ilustra el uso de la regresión logarítmica lineal de Poisson en el conjunto de datos de reclamaciones de responsabilidad civil de automóviles de Francia <https://www.openml.org/d/41214>`_ de 1 y lo compara con un modelo lineal ajustado con el error mínimo cuadrático habitual y un modelo no lineal GBRT ajustado con la pérdida de Poisson (y un enlace logarítmico).
Unas cuantas definiciones:
Una póliza es un contrato entre una compañía de seguros y un individuo: el tomador del seguro, es decir, el conductor del vehículo en este caso.
Un reclamo es la petición que hace el asegurado a la aseguradora para que le indemnice por un siniestro cubierto por el seguro.
La exposición es la duración de la cobertura del seguro de una determinada póliza, en años.
La frecuencia de los siniestros es el número de siniestros dividido por la exposición, que suele medirse en número de siniestros por año.
En este conjunto de datos, cada muestra corresponde a una póliza de seguro. Las características disponibles incluyen la edad del conductor, la edad del vehículo, la potencia del vehículo, etc.
Nuestro objetivo es predecir la frecuencia esperada de siniestros tras un accidente de coche para un nuevo asegurado, dados los datos históricos sobre una población de asegurados.
- 1
A. Noll, R. Salzmann and M.V. Wuthrich, Case Study: French Motor Third-Party Liability Claims (November 8, 2018). doi:10.2139/ssrn.3164764
print(__doc__)
# Authors: Christian Lorentzen <lorentzen.ch@gmail.com>
# Roman Yurchak <rth.yurchak@gmail.com>
# Olivier Grisel <olivier.grisel@ensta.org>
# License: BSD 3 clause
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
El conjunto de datos de siniestros de responsabilidad civil del automóvil en Francia¶
Carguemos el conjunto de datos de siniestros de automóviles desde OpenML: https://www.openml.org/d/41214
from sklearn.datasets import fetch_openml
df = fetch_openml(data_id=41214, as_frame=True).frame
df
Out:
/home/mapologo/miniconda3/envs/sklearn/lib/python3.9/site-packages/scikit_learn-0.24.1-py3.9-linux-x86_64.egg/sklearn/datasets/_openml.py:849: UserWarning: Version 1 of dataset freMTPL2freq is inactive, meaning that issues have been found in the dataset. Try using a newer version from this URL: https://www.openml.org/data/v1/download/20649148/freMTPL2freq.arff
warn("Version {} of dataset {} is inactive, meaning that issues have "
El número de siniestros (ClaimNb) es un número entero positivo que puede modelarse como una distribución de Poisson. Se supone entonces que es el número de eventos discretos que ocurren con una tasa constante en un intervalo de tiempo determinado (Exposure, en unidades de años).
Aquí queremos modelar la frecuencia y = ClaimNb / Exposure condicionada a X mediante una distribución de Poisson (escalada), y utilizar Exposure como sample_weight.
df["Frequency"] = df["ClaimNb"] / df["Exposure"]
print("Average Frequency = {}"
.format(np.average(df["Frequency"], weights=df["Exposure"])))
print("Fraction of exposure with zero claims = {0:.1%}"
.format(df.loc[df["ClaimNb"] == 0, "Exposure"].sum() /
df["Exposure"].sum()))
fig, (ax0, ax1, ax2) = plt.subplots(ncols=3, figsize=(16, 4))
ax0.set_title("Number of claims")
_ = df["ClaimNb"].hist(bins=30, log=True, ax=ax0)
ax1.set_title("Exposure in years")
_ = df["Exposure"].hist(bins=30, log=True, ax=ax1)
ax2.set_title("Frequency (number of claims per year)")
_ = df["Frequency"].hist(bins=30, log=True, ax=ax2)
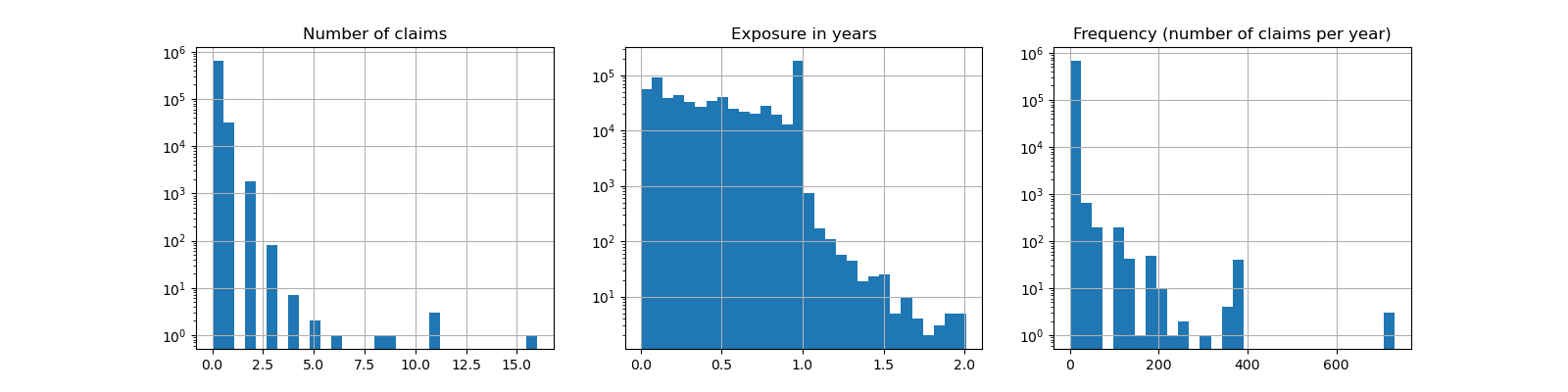
Out:
Average Frequency = 0.10070308464041304
Fraction of exposure with zero claims = 93.9%
Las columnas restantes pueden utilizarse para predecir la frecuencia de los siniestros. Esas columnas son muy heterogéneas con una mezcla de variables categóricas y numéricas con diferentes escalas, posiblemente muy desigualmente distribuidas.
Por lo tanto, para ajustar los modelos lineales con esos predictores es necesario realizar las transformaciones estándar de las características, como se indica a continuación:
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import FunctionTransformer, OneHotEncoder
from sklearn.preprocessing import StandardScaler, KBinsDiscretizer
from sklearn.compose import ColumnTransformer
log_scale_transformer = make_pipeline(
FunctionTransformer(np.log, validate=False),
StandardScaler()
)
linear_model_preprocessor = ColumnTransformer(
[
("passthrough_numeric", "passthrough",
["BonusMalus"]),
("binned_numeric", KBinsDiscretizer(n_bins=10),
["VehAge", "DrivAge"]),
("log_scaled_numeric", log_scale_transformer,
["Density"]),
("onehot_categorical", OneHotEncoder(),
["VehBrand", "VehPower", "VehGas", "Region", "Area"]),
],
remainder="drop",
)
Una línea de base de predicción constante¶
Cabe destacar que más del 93% de los asegurados tienen cero siniestros. Si convirtiéramos este problema en una tarea de clasificación binaria, estaría significativamente desequilibrado, e incluso un modelo simplista que sólo predijera la media puede alcanzar una precisión del 93%.
Para evaluar la pertinencia de las métricas utilizadas, consideraremos como línea de base un estimador «ficticio» que predice constantemente la frecuencia media de la muestra de entrenamiento.
from sklearn.dummy import DummyRegressor
from sklearn.pipeline import Pipeline
from sklearn.model_selection import train_test_split
df_train, df_test = train_test_split(df, test_size=0.33, random_state=0)
dummy = Pipeline([
("preprocessor", linear_model_preprocessor),
("regressor", DummyRegressor(strategy='mean')),
]).fit(df_train, df_train["Frequency"],
regressor__sample_weight=df_train["Exposure"])
Calculemos el rendimiento de esta línea de base de predicción constante con 3 métricas de regresión diferentes:
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_poisson_deviance
def score_estimator(estimator, df_test):
"""Score an estimator on the test set."""
y_pred = estimator.predict(df_test)
print("MSE: %.3f" %
mean_squared_error(df_test["Frequency"], y_pred,
sample_weight=df_test["Exposure"]))
print("MAE: %.3f" %
mean_absolute_error(df_test["Frequency"], y_pred,
sample_weight=df_test["Exposure"]))
# Ignore non-positive predictions, as they are invalid for
# the Poisson deviance.
mask = y_pred > 0
if (~mask).any():
n_masked, n_samples = (~mask).sum(), mask.shape[0]
print(f"WARNING: Estimator yields invalid, non-positive predictions "
f" for {n_masked} samples out of {n_samples}. These predictions "
f"are ignored when computing the Poisson deviance.")
print("mean Poisson deviance: %.3f" %
mean_poisson_deviance(df_test["Frequency"][mask],
y_pred[mask],
sample_weight=df_test["Exposure"][mask]))
print("Constant mean frequency evaluation:")
score_estimator(dummy, df_test)
Out:
Constant mean frequency evaluation:
MSE: 0.564
MAE: 0.189
mean Poisson deviance: 0.625
Modelos lineales (generalizados)¶
Comenzamos modelando la variable objetivo con el modelo de regresión lineal por mínimos cuadrados (l2 penalizado), más conocido como regresión Ridge. Utilizamos una penalización alpha baja, ya que esperamos que un modelo lineal de este tipo no se ajuste a un conjunto de datos tan grande.
La desviación de Poisson no puede calcularse sobre los valores no positivos predichos por el modelo. Para los modelos que devuelven algunas predicciones no positivas (por ejemplo, Ridge) ignoramos las muestras correspondientes, lo que significa que la desviación de Poisson obtenida es aproximada. Un enfoque alternativo podría ser utilizar el metaestimador TransformedTargetRegressor para asignar y_pred a un dominio estrictamente positivo.
print("Ridge evaluation:")
score_estimator(ridge_glm, df_test)
Out:
Ridge evaluation:
MSE: 0.560
MAE: 0.177
WARNING: Estimator yields invalid, non-positive predictions for 1315 samples out of 223745. These predictions are ignored when computing the Poisson deviance.
mean Poisson deviance: 0.601
A continuación, ajustamos el regresor de Poisson a la variable objetivo. Fijamos la fuerza de regularización alpha a aproximadamente 1e-6 sobre el número de muestras (es decir, 1e-12) para imitar el regresor Ridge cuyo término de penalización L2 escala de forma diferente con el número de muestras.
Dado que el regresor de Poisson modela internamente el logaritmo del valor objetivo esperado en lugar del valor esperado directamente (función de enlace logarítmica frente a identidad), la relación entre X e y ya no es exactamente lineal. Por lo tanto, el regresor de Poisson se denomina modelo lineal generalizado (GLM) en lugar de un modelo lineal simple como es el caso de la regresión Ridge.
from sklearn.linear_model import PoissonRegressor
n_samples = df_train.shape[0]
poisson_glm = Pipeline([
("preprocessor", linear_model_preprocessor),
("regressor", PoissonRegressor(alpha=1e-12, max_iter=300))
])
poisson_glm.fit(df_train, df_train["Frequency"],
regressor__sample_weight=df_train["Exposure"])
print("PoissonRegressor evaluation:")
score_estimator(poisson_glm, df_test)
Out:
PoissonRegressor evaluation:
MSE: 0.560
MAE: 0.186
mean Poisson deviance: 0.594
Árboles de regresión con potenciación de gradiente para la regresión de Poisson¶
Por último, consideraremos un modelo no lineal, a saber, los árboles de regresión con potenciación de gradiente. Los modelos basados en árboles no requieren que los datos categóricos estén codificados en un solo punto: en su lugar, podemos codificar cada etiqueta de categoría con un número entero arbitrario utilizando OrdinalEncoder. Con esta codificación, los árboles tratarán las características categóricas como características ordenadas, lo que podría no ser siempre un comportamiento deseado. Sin embargo, este efecto es limitado para los árboles suficientemente profundos que son capaces de recuperar la naturaleza categórica de las características. La principal ventaja del OrdinalEncoder sobre el OneHotEncoder es que el entrenamiento será más rápido.
La potenciación de gradiente también ofrece la posibilidad de ajustar los árboles con una pérdida de Poisson (con una función implícita de enlace logarítmico) en lugar de la pérdida por defecto por mínimos cuadrados. Aquí sólo ajustamos los árboles con la pérdida de Poisson para mantener este ejemplo conciso.
from sklearn.experimental import enable_hist_gradient_boosting # noqa
from sklearn.ensemble import HistGradientBoostingRegressor
from sklearn.preprocessing import OrdinalEncoder
tree_preprocessor = ColumnTransformer(
[
("categorical", OrdinalEncoder(),
["VehBrand", "VehPower", "VehGas", "Region", "Area"]),
("numeric", "passthrough",
["VehAge", "DrivAge", "BonusMalus", "Density"]),
],
remainder="drop",
)
poisson_gbrt = Pipeline([
("preprocessor", tree_preprocessor),
("regressor", HistGradientBoostingRegressor(loss="poisson",
max_leaf_nodes=128)),
])
poisson_gbrt.fit(df_train, df_train["Frequency"],
regressor__sample_weight=df_train["Exposure"])
print("Poisson Gradient Boosted Trees evaluation:")
score_estimator(poisson_gbrt, df_test)
Out:
Poisson Gradient Boosted Trees evaluation:
MSE: 0.567
MAE: 0.183
mean Poisson deviance: 0.575
Al igual que el MLG de Poisson anterior, el modelo de árboles con refuerzo de gradiente minimiza la desviación de Poisson. Sin embargo, debido a un mayor poder de predicción, alcanza valores más bajos de desviación de Poisson.
La evaluación de modelos con una única división de entrenamiento/prueba es propensa a fluctuaciones aleatorias. Si los recursos informáticos lo permiten, habría que comprobar que las métricas de rendimiento con validación cruzada llevarían a conclusiones similares.
La diferencia cualitativa entre estos modelos también puede visualizarse comparando el histograma de los valores objetivo observados con el de los valores predichos:
fig, axes = plt.subplots(nrows=2, ncols=4, figsize=(16, 6), sharey=True)
fig.subplots_adjust(bottom=0.2)
n_bins = 20
for row_idx, label, df in zip(range(2),
["train", "test"],
[df_train, df_test]):
df["Frequency"].hist(bins=np.linspace(-1, 30, n_bins),
ax=axes[row_idx, 0])
axes[row_idx, 0].set_title("Data")
axes[row_idx, 0].set_yscale('log')
axes[row_idx, 0].set_xlabel("y (observed Frequency)")
axes[row_idx, 0].set_ylim([1e1, 5e5])
axes[row_idx, 0].set_ylabel(label + " samples")
for idx, model in enumerate([ridge_glm, poisson_glm, poisson_gbrt]):
y_pred = model.predict(df)
pd.Series(y_pred).hist(bins=np.linspace(-1, 4, n_bins),
ax=axes[row_idx, idx+1])
axes[row_idx, idx + 1].set(
title=model[-1].__class__.__name__,
yscale='log',
xlabel="y_pred (predicted expected Frequency)"
)
plt.tight_layout()
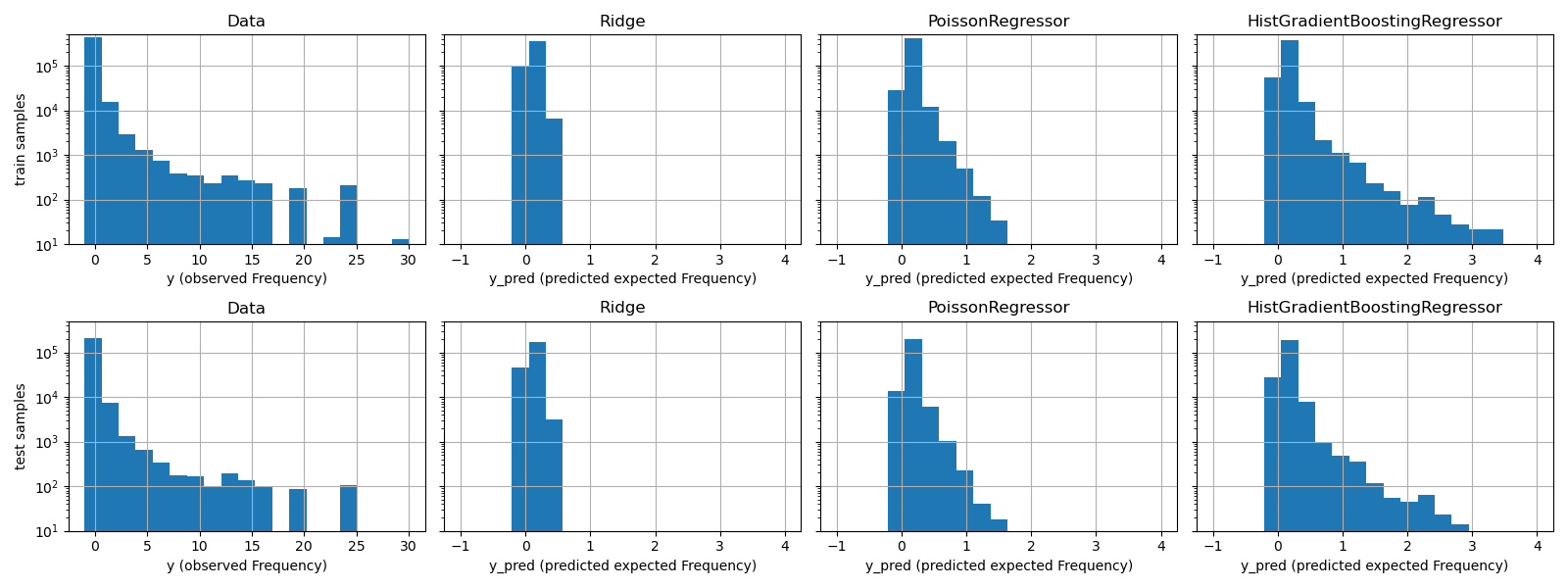
Los datos experimentales presentan una distribución de cola larga para y. En todos los modelos, predecimos la frecuencia esperada de una variable aleatoria, por lo que tendremos necesariamente menos valores extremos que para las realizaciones observadas de esa variable aleatoria. Esto explica que la moda de los histogramas de las predicciones del modelo no corresponda necesariamente al valor más pequeño. Además, la distribución normal utilizada en Ridge tiene una varianza constante, mientras que para la distribución Poisson utilizada en PoissonRegressor y HistGradientBoostingRegressor, la varianza es proporcional al valor esperado predicho.
Por lo tanto, entre los estimadores considerados, PoissonRegressor y HistGradientBoostingRegressor son a priori más adecuadas para modelar la distribución de la cola larga de los datos no negativos en comparación con el modelo Ridge que hace una suposición errónea sobre la distribución de la variable objetivo.
El estimador HistGradientBoostingRegressor es el más flexible y puede predecir valores esperados más altos.
Ten en cuenta que podríamos haber utilizado la pérdida de mínimos cuadrados para el modelo HistGradientBoostingRegressor. Esto supondría erróneamente una variable de respuesta de distribución normal, como hace el modelo Ridge, y posiblemente también llevaría a predicciones ligeramente negativas. Sin embargo, los árboles con potenciación de gradiente seguirían funcionando relativamente bien y, en particular, mejor que PoissonRegressor gracias a la flexibilidad de los árboles combinada con el gran número de muestras de entrenamiento.
Evaluación de la calibración de las predicciones¶
Para garantizar que los estimadores ofrezcan predicciones razonables para los distintos tipos de asegurados, podemos clasificar las muestras de prueba en función de y_pred devuelta por cada modelo. Luego, para cada intervalo, comparamos la media de las predicciones de y_pred con la media del objetivo observado:
from sklearn.utils import gen_even_slices
def _mean_frequency_by_risk_group(y_true, y_pred, sample_weight=None,
n_bins=100):
"""Compare predictions and observations for bins ordered by y_pred.
We order the samples by ``y_pred`` and split it in bins.
In each bin the observed mean is compared with the predicted mean.
Parameters
----------
y_true: array-like of shape (n_samples,)
Ground truth (correct) target values.
y_pred: array-like of shape (n_samples,)
Estimated target values.
sample_weight : array-like of shape (n_samples,)
Sample weights.
n_bins: int
Number of bins to use.
Returns
-------
bin_centers: ndarray of shape (n_bins,)
bin centers
y_true_bin: ndarray of shape (n_bins,)
average y_pred for each bin
y_pred_bin: ndarray of shape (n_bins,)
average y_pred for each bin
"""
idx_sort = np.argsort(y_pred)
bin_centers = np.arange(0, 1, 1/n_bins) + 0.5/n_bins
y_pred_bin = np.zeros(n_bins)
y_true_bin = np.zeros(n_bins)
for n, sl in enumerate(gen_even_slices(len(y_true), n_bins)):
weights = sample_weight[idx_sort][sl]
y_pred_bin[n] = np.average(
y_pred[idx_sort][sl], weights=weights
)
y_true_bin[n] = np.average(
y_true[idx_sort][sl],
weights=weights
)
return bin_centers, y_true_bin, y_pred_bin
print(f"Actual number of claims: {df_test['ClaimNb'].sum()}")
fig, ax = plt.subplots(nrows=2, ncols=2, figsize=(12, 8))
plt.subplots_adjust(wspace=0.3)
for axi, model in zip(ax.ravel(), [ridge_glm, poisson_glm, poisson_gbrt,
dummy]):
y_pred = model.predict(df_test)
y_true = df_test["Frequency"].values
exposure = df_test["Exposure"].values
q, y_true_seg, y_pred_seg = _mean_frequency_by_risk_group(
y_true, y_pred, sample_weight=exposure, n_bins=10)
# Name of the model after the estimator used in the last step of the
# pipeline.
print(f"Predicted number of claims by {model[-1]}: "
f"{np.sum(y_pred * exposure):.1f}")
axi.plot(q, y_pred_seg, marker='x', linestyle="--", label="predictions")
axi.plot(q, y_true_seg, marker='o', linestyle="--", label="observations")
axi.set_xlim(0, 1.0)
axi.set_ylim(0, 0.5)
axi.set(
title=model[-1],
xlabel='Fraction of samples sorted by y_pred',
ylabel='Mean Frequency (y_pred)'
)
axi.legend()
plt.tight_layout()
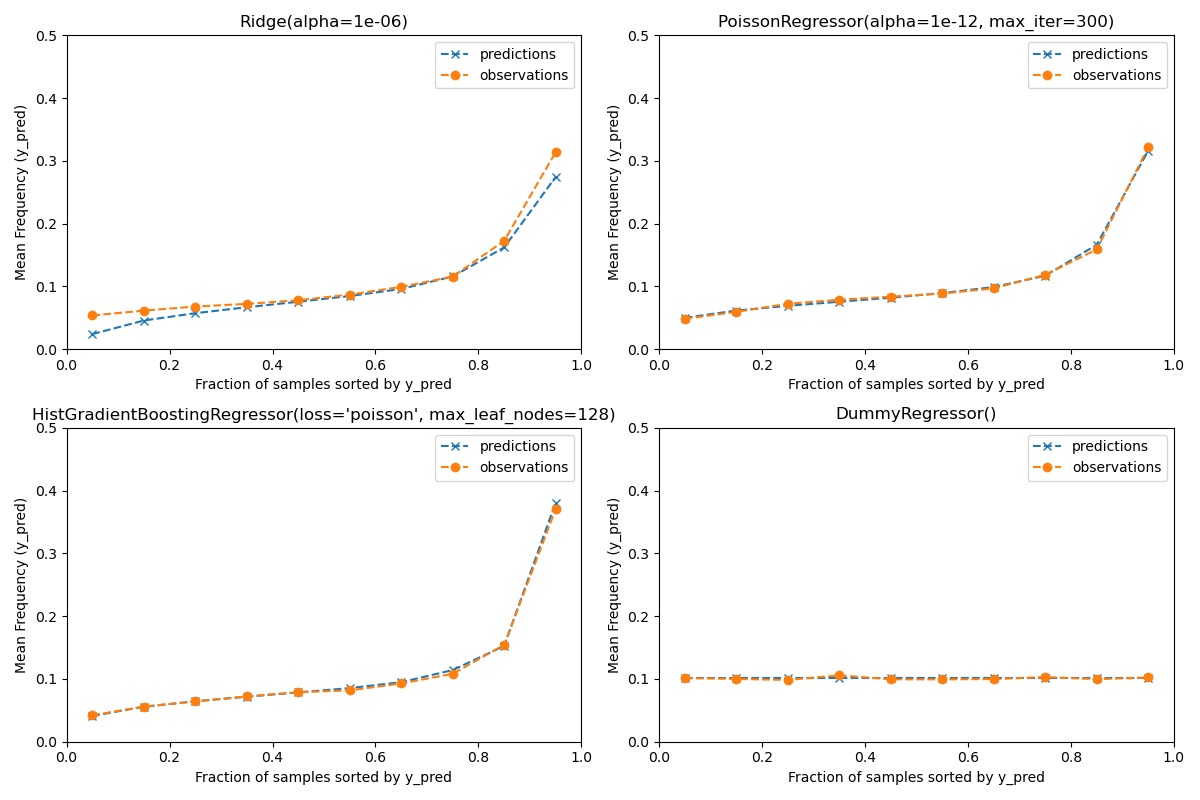
Out:
Actual number of claims: 11935.0
Predicted number of claims by Ridge(alpha=1e-06): 10692.7
Predicted number of claims by PoissonRegressor(alpha=1e-12, max_iter=300): 11924.4
Predicted number of claims by HistGradientBoostingRegressor(loss='poisson', max_leaf_nodes=128): 12112.9
Predicted number of claims by DummyRegressor(): 11931.2
El modelo de regresión dummy predice una frecuencia constante. Este modelo no atribuye el mismo rango ligado a todas las muestras, pero está sin embargo globalmente bien calibrado (para estimar la frecuencia media de toda la población).
El modelo de regresión «Ridge» puede predecir frecuencias esperadas muy bajas que no se correspondan a los datos. Por tanto, puede subestimar gravemente el riesgo de algunos asegurados.
El PoissonRegressor y el HistGradientBoostingRegressor muestran una mejor consistencia entre los objetivos predichos y los observados, especialmente para los valores bajos de los objetivos predichos.
La suma de todas las predicciones también confirma el problema de calibración del modelo Ridge: subestima en más de un 3% el número total de siniestros del conjunto de pruebas, mientras que los otros tres modelos pueden recuperar aproximadamente el número total de siniestros de la cartera de pruebas.
Evaluación del poder de clasificación¶
Para algunas aplicaciones empresariales, nos interesa la capacidad del modelo para clasificar a los asegurados más arriesgados de los más seguros, independientemente del valor absoluto de la predicción. En este caso, la evaluación del modelo convertiría el problema en un problema de clasificación en lugar de un problema de regresión.
Para comparar los 3 modelos desde esta perspectiva, se puede trazar la proporción acumulativa de siniestros frente a la proporción acumulativa de exposición para las muestras de prueba ordenadas por las predicciones del modelo, de la más segura a la más arriesgada según cada modelo.
Este gráfico se denomina curva de Lorenz y puede resumirse con el índice de Gini:
from sklearn.metrics import auc
def lorenz_curve(y_true, y_pred, exposure):
y_true, y_pred = np.asarray(y_true), np.asarray(y_pred)
exposure = np.asarray(exposure)
# order samples by increasing predicted risk:
ranking = np.argsort(y_pred)
ranked_frequencies = y_true[ranking]
ranked_exposure = exposure[ranking]
cumulated_claims = np.cumsum(ranked_frequencies * ranked_exposure)
cumulated_claims /= cumulated_claims[-1]
cumulated_exposure = np.cumsum(ranked_exposure)
cumulated_exposure /= cumulated_exposure[-1]
return cumulated_exposure, cumulated_claims
fig, ax = plt.subplots(figsize=(8, 8))
for model in [dummy, ridge_glm, poisson_glm, poisson_gbrt]:
y_pred = model.predict(df_test)
cum_exposure, cum_claims = lorenz_curve(df_test["Frequency"], y_pred,
df_test["Exposure"])
gini = 1 - 2 * auc(cum_exposure, cum_claims)
label = "{} (Gini: {:.2f})".format(model[-1], gini)
ax.plot(cum_exposure, cum_claims, linestyle="-", label=label)
# Oracle model: y_pred == y_test
cum_exposure, cum_claims = lorenz_curve(df_test["Frequency"],
df_test["Frequency"],
df_test["Exposure"])
gini = 1 - 2 * auc(cum_exposure, cum_claims)
label = "Oracle (Gini: {:.2f})".format(gini)
ax.plot(cum_exposure, cum_claims, linestyle="-.", color="gray", label=label)
# Random Baseline
ax.plot([0, 1], [0, 1], linestyle="--", color="black",
label="Random baseline")
ax.set(
title="Lorenz curves by model",
xlabel='Cumulative proportion of exposure (from safest to riskiest)',
ylabel='Cumulative proportion of claims'
)
ax.legend(loc="upper left")
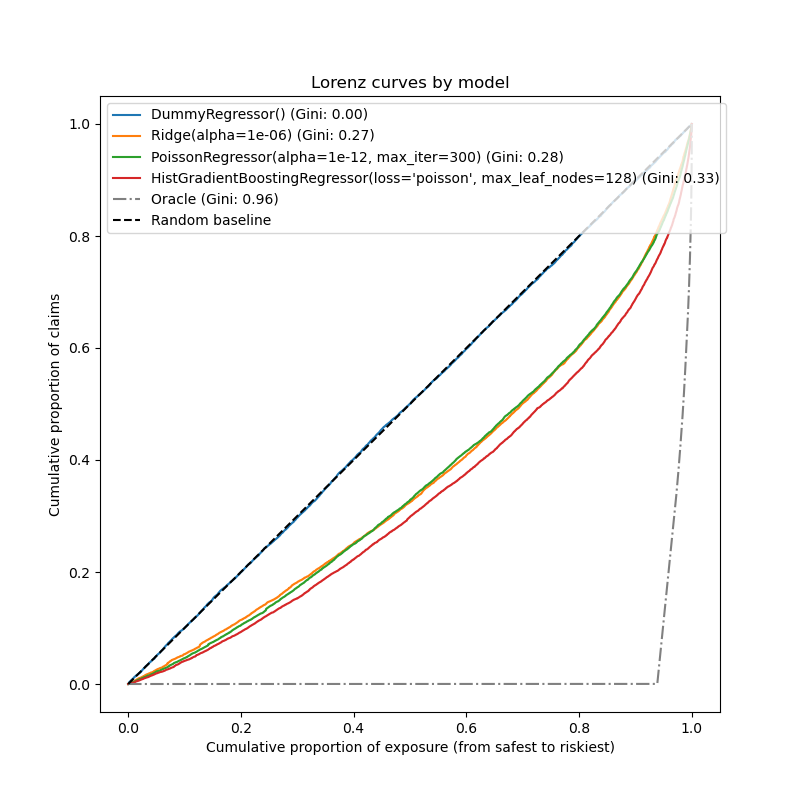
Out:
<matplotlib.legend.Legend object at 0x7f2c1e763760>
Como era de esperar, el regresor ficticio es incapaz de clasificar correctamente las muestras y, por tanto, es el que peor funciona en este gráfico.
El modelo basado en el árbol es significativamente mejor a la hora de clasificar a los asegurados por riesgo, mientras que los dos modelos lineales tienen un rendimiento similar.
Los tres modelos son significativamente mejores que el azar, pero también están muy lejos de hacer predicciones perfectas.
Este último punto es esperable debido a la naturaleza del problema: la ocurrencia de accidentes está dominada en su mayoría por causas circunstanciales que no se recogen en las columnas del conjunto de datos y que, de hecho, pueden considerarse puramente aleatorias.
Los modelos lineales asumen que no hay interacciones entre las variables de entrada, lo que probablemente provoca un ajuste insuficiente. La inserción de un extractor de características polinómicas (PolynomialFeatures) aumenta efectivamente su poder de discriminación en 2 puntos del índice de Gini. En particular, mejora la capacidad de los modelos para identificar el 5% de los perfiles.
Principales conclusiones¶
El rendimiento de los modelos puede evaluarse por su capacidad de producir predicciones bien calibradas y una buena clasificación.
La calibración del modelo puede evaluarse graficando el valor medio observado frente al valor medio previsto en grupos de muestras de prueba clasificados por riesgo previsto.
La pérdida por mínimos cuadrados (junto con el uso implícito de la función de enlace de identidad) del modelo de regresión Ridge parece hacer que este modelo esté mal calibrado. En particular, tiende a subestimar el riesgo y puede incluso predecir frecuencias negativas no válidas.
El uso de la pérdida de Poisson con un enlace logarítmico puede corregir estos problemas y conducir a un modelo lineal bien calibrado.
El índice de Gini refleja la capacidad de un modelo para clasificar las predicciones con independencia de sus valores absolutos, por lo que sólo evalúa su poder de clasificación.
A pesar de la mejora en la calibración, el poder de clasificación de ambos modelos lineales es comparable y está muy por debajo del poder de clasificación de los árboles de regresión de potenciación de gradiente.
La desviación de Poisson calculada como métrica de evaluación refleja tanto la calibración como el poder de clasificación del modelo. También hace una suposición lineal sobre la relación ideal entre el valor esperado y la varianza de la variable de respuesta. En aras de la concisión, no comprobamos si este supuesto se cumple.
Las métricas de regresión tradicionales, como el error cuadrático medio y el error absoluto medio, son difíciles de interpretar de forma significativa en valores de recuento con muchos ceros.
plt.show()
Tiempo total de ejecución del script: (1 minutos 35.081 segundos)
