Regresión de Theil-Sen

Calcula una regresión de Theil-Sen en un conjunto de datos sintéticos.

Ver Estimador Theil-Sen: estimador basado en la mediana generalizada para más información sobre el regresor.

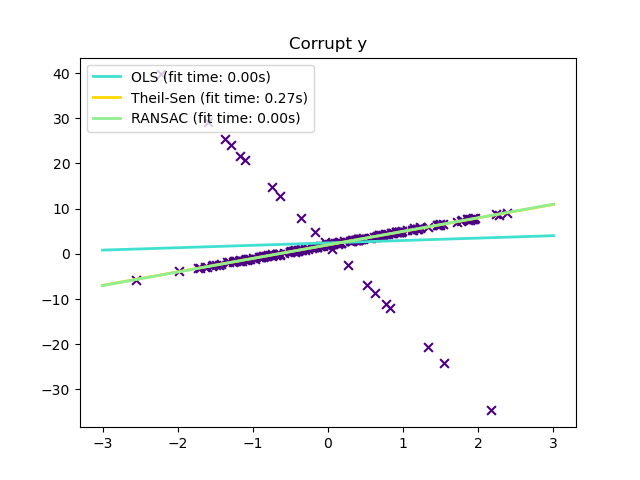
En comparación con el estimador OLS (mínimos cuadrados ordinarios), el estimador Theil-Sen es robusto frente a los valores atípicos. Tiene un punto de ruptura de aproximadamente el 29,3% en el caso de una regresión lineal simple, lo que significa que puede tolerar datos corruptos arbitrarios (valores atípicos) de hasta el 29,3% en el caso bidimensional.

La estimación del modelo se realiza calculando las pendientes y los interceptos de una subpoblación de todas las combinaciones posibles de p puntos de submuestra. Si se ajusta un intercepto, p debe ser mayor o igual que n_features + 1. La pendiente y el intercepto finales se definen entonces como la mediana espacial de estas pendientes e interceptos.

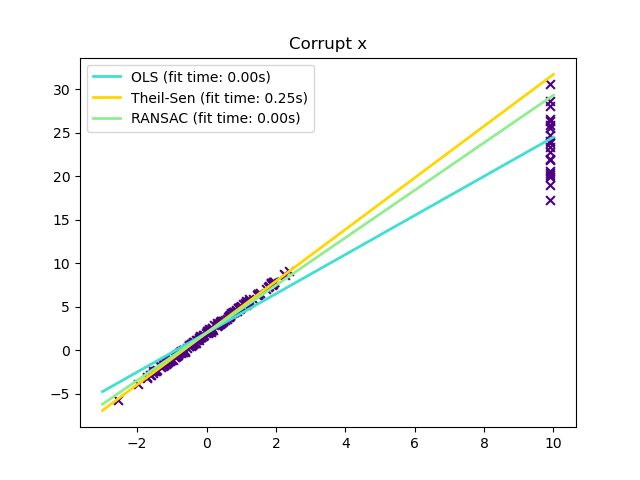
En algunos casos, Theil-Sen funciona mejor que RANSAC, que también es un método robusto. Esto se ilustra en el segundo ejemplo siguiente, en el que los valores atípicos con respecto al eje x perturban a RANSAC. El ajuste del parámetro residual_threshold de RANSAC lo remedia, pero en general se necesita un conocimiento a priori sobre los datos y la naturaleza de los valores atípicos. Debido a la complejidad computacional de Theil-Sen, se recomienda utilizarlo sólo para problemas pequeños en términos de número de muestras y características. Para problemas más grandes, el parámetro max_subpopulation restringe la magnitud de todas las combinaciones posibles de p puntos de submuestra a un subconjunto elegido al azar y, por tanto, también limita el tiempo de ejecución. Por lo tanto, Theil-Sen es aplicable a problemas más grandes con el inconveniente de perder algunas de sus propiedades matemáticas, ya que entonces trabaja sobre un subconjunto aleatorio.

• 
• 

# Author: Florian Wilhelm -- <florian.wilhelm@gmail.com>
# License: BSD 3 clause

import time
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression, TheilSenRegressor
from sklearn.linear_model import RANSACRegressor

print(__doc__)

estimators = [('OLS', LinearRegression()),
              ('Theil-Sen', TheilSenRegressor(random_state=42)),
              ('RANSAC', RANSACRegressor(random_state=42)), ]
colors = {'OLS': 'turquoise', 'Theil-Sen': 'gold', 'RANSAC': 'lightgreen'}
lw = 2

# #############################################################################
# Outliers only in the y direction

np.random.seed(0)
n_samples = 200
# Linear model y = 3*x + N(2, 0.1**2)
x = np.random.randn(n_samples)
w = 3.
c = 2.
noise = 0.1 * np.random.randn(n_samples)
y = w * x + c + noise
# 10% outliers
y[-20:] += -20 * x[-20:]
X = x[:, np.newaxis]

plt.scatter(x, y, color='indigo', marker='x', s=40)
line_x = np.array([-3, 3])
for name, estimator in estimators:
    t0 = time.time()
    estimator.fit(X, y)
    elapsed_time = time.time() - t0
    y_pred = estimator.predict(line_x.reshape(2, 1))
    plt.plot(line_x, y_pred, color=colors[name], linewidth=lw,
             label='%s (fit time: %.2fs)' % (name, elapsed_time))

plt.axis('tight')
plt.legend(loc='upper left')
plt.title("Corrupt y")

# #############################################################################
# Outliers in the X direction

np.random.seed(0)
# Linear model y = 3*x + N(2, 0.1**2)
x = np.random.randn(n_samples)
noise = 0.1 * np.random.randn(n_samples)
y = 3 * x + 2 + noise
# 10% outliers
x[-20:] = 9.9
y[-20:] += 22
X = x[:, np.newaxis]

plt.figure()
plt.scatter(x, y, color='indigo', marker='x', s=40)

line_x = np.array([-3, 10])
for name, estimator in estimators:
    t0 = time.time()
    estimator.fit(X, y)
    elapsed_time = time.time() - t0
    y_pred = estimator.predict(line_x.reshape(2, 1))
    plt.plot(line_x, y_pred, color=colors[name], linewidth=lw,
             label='%s (fit time: %.2fs)' % (name, elapsed_time))

plt.axis('tight')
plt.legend(loc='upper left')
plt.title("Corrupt x")
plt.show()