Ajuste de curvas con regresión Bayesiana Ridge

Calcula una regresión Bayesiana Ridge de Sinusoides.

Consulta Regresión Bayesiana de Cresta para más información sobre el regresor.

En general, cuando se ajusta una curva con un polinomio mediante la regresión de cresta bayesiana, la selección de los valores iniciales de los parámetros de regularización (alfa, lambda) puede ser importante. Esto se debe a que los parámetros de regularización se determinan mediante un procedimiento iterativo que depende de los valores iniciales.

En este ejemplo, la sinusoide se aproxima mediante un polinomio utilizando diferentes pares de valores iniciales.

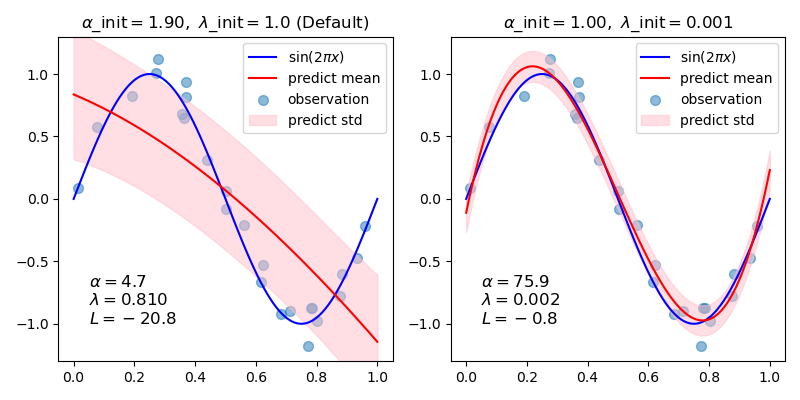
Cuando se parte de los valores por defecto (alpha_init = 1.90, lambda_init = 1.), el sesgo de la curva resultante es grande, y la varianza es pequeña. Por lo tanto, lambda_init debe ser relativamente pequeña (1.e-3) para reducir el sesgo.

Además, evaluando la verosimilitud marginal logarítmica (L) de estos modelos, podemos determinar cuál es mejor. Se puede concluir que el modelo con mayor L es más probable.

print(__doc__)

# Author: Yoshihiro Uchida <nimbus1after2a1sun7shower@gmail.com>

import numpy as np
import matplotlib.pyplot as plt

from sklearn.linear_model import BayesianRidge


def func(x): return np.sin(2*np.pi*x)


# #############################################################################
# Generate sinusoidal data with noise
size = 25
rng = np.random.RandomState(1234)
x_train = rng.uniform(0., 1., size)
y_train = func(x_train) + rng.normal(scale=0.1, size=size)
x_test = np.linspace(0., 1., 100)


# #############################################################################
# Fit by cubic polynomial
n_order = 3
X_train = np.vander(x_train, n_order + 1, increasing=True)
X_test = np.vander(x_test, n_order + 1, increasing=True)

# #############################################################################
# Plot the true and predicted curves with log marginal likelihood (L)
reg = BayesianRidge(tol=1e-6, fit_intercept=False, compute_score=True)
fig, axes = plt.subplots(1, 2, figsize=(8, 4))
for i, ax in enumerate(axes):
    # Bayesian ridge regression with different initial value pairs
    if i == 0:
        init = [1 / np.var(y_train), 1.]  # Default values
    elif i == 1:
        init = [1., 1e-3]
        reg.set_params(alpha_init=init[0], lambda_init=init[1])
    reg.fit(X_train, y_train)
    ymean, ystd = reg.predict(X_test, return_std=True)

    ax.plot(x_test, func(x_test), color="blue", label="sin($2\\pi x$)")
    ax.scatter(x_train, y_train, s=50, alpha=0.5, label="observation")
    ax.plot(x_test, ymean, color="red", label="predict mean")
    ax.fill_between(x_test, ymean-ystd, ymean+ystd,
                    color="pink", alpha=0.5, label="predict std")
    ax.set_ylim(-1.3, 1.3)
    ax.legend()
    title = "$\\alpha$_init$={:.2f},\\ \\lambda$_init$={}$".format(
            init[0], init[1])
    if i == 0:
        title += " (Default)"
    ax.set_title(title, fontsize=12)
    text = "$\\alpha={:.1f}$\n$\\lambda={:.3f}$\n$L={:.1f}$".format(
           reg.alpha_, reg.lambda_, reg.scores_[-1])
    ax.text(0.05, -1.0, text, fontsize=12)

plt.tight_layout()
plt.show()