Interpolación polinómica

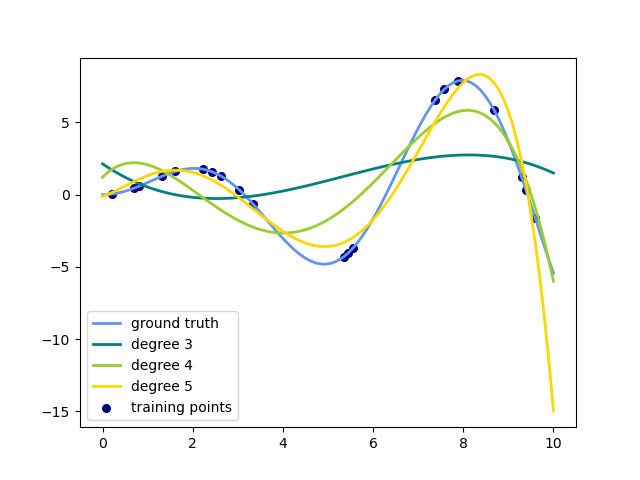
Este ejemplo demuestra cómo aproximar una función con un polinomio de grado n_degree utilizando la regresión de cresta. Concretamente, a partir de n_samples 1d puntos, basta con construir la matriz de Vandermonde, que es n_samples x n_degree+1 y tiene la siguiente forma:

[[1, x_1, x_1 ** 2, x_1 ** 3, …],

[1, x_2, x_2 ** 2, x_2 ** 3, …], …]

Intuitivamente, esta matriz puede interpretarse como una matriz de pseudo características (los puntos elevados a alguna potencia). La matriz es similar (pero diferente) a la matriz inducida por un núcleo polinómico.

Este ejemplo muestra que se puede hacer una regresión no lineal con un modelo lineal, utilizando una pipeline para añadir características no lineales. Los métodos kernel amplían esta idea y pueden inducir espacios de características de muy alta (incluso infinita) dimensión.

print(__doc__)

# Author: Mathieu Blondel
#         Jake Vanderplas
# License: BSD 3 clause

import numpy as np
import matplotlib.pyplot as plt

from sklearn.linear_model import Ridge
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline


def f(x):
    """ function to approximate by polynomial interpolation"""
    return x * np.sin(x)


# generate points used to plot
x_plot = np.linspace(0, 10, 100)

# generate points and keep a subset of them
x = np.linspace(0, 10, 100)
rng = np.random.RandomState(0)
rng.shuffle(x)
x = np.sort(x[:20])
y = f(x)

# create matrix versions of these arrays
X = x[:, np.newaxis]
X_plot = x_plot[:, np.newaxis]

colors = ['teal', 'yellowgreen', 'gold']
lw = 2
plt.plot(x_plot, f(x_plot), color='cornflowerblue', linewidth=lw,
         label="ground truth")
plt.scatter(x, y, color='navy', s=30, marker='o', label="training points")

for count, degree in enumerate([3, 4, 5]):
    model = make_pipeline(PolynomialFeatures(degree), Ridge())
    model.fit(X, y)
    y_plot = model.predict(X_plot)
    plt.plot(x_plot, y_plot, color=colors[count], linewidth=lw,
             label="degree %d" % degree)

plt.legend(loc='lower left')

plt.show()