sklearn.linear_model.LassoLarsIC

class sklearn.linear_model.LassoLarsIC

Ajuste del modelo Lasso con Lars utilizando BIC o AIC para la selección del modelo

El objetivo de optimización para Lasso es:

(1 / (2 * n_samples)) * ||y - Xw||^2_2 + alpha * ||w||_1

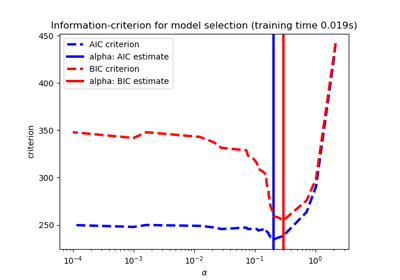
El AIC es el criterio de información de Akaike y el BIC es el criterio de Información de Bayes. Estos criterios son útiles para seleccionar el valor del parámetro de regularización haciendo una compensación entre la bondad del ajuste y la complejidad del modelo. Un buen modelo debe explicar bien los datos y al mismo tiempo ser sencillo.

Lee más en el Manual de usuario.

Parámetros

criterion{“bic” , “aic”}, default=”aic”

El tipo de criterio a utilizar.

fit_interceptbool, default=True

si se calcula el intercepto para este modelo. Si se establece en False, no se utilizará ningún intercepto en los cálculos (es decir, se espera que los datos estén centrados).

verbosebool o int, default=False

Establece la cantidad de verbosidad.

normalizebool, default=True

Este parámetro es ignorado cuando fit_intercept se establece en False. Si es True, los regresores X serán normalizados antes de la regresión restando la media y dividiendo por la norma l2. Si deseas estandarizar, por favor utiliza StandardScaler antes de invocar a fit en un estimador con normalize=False.

precomputebool, “auto” o array-like, default=”auto”

Si se utiliza una matriz de Gram precalculada para acelerar los cálculos. Si se establece como 'auto' podemos decidir. La matriz de Gram también se puede pasar como argumento.

max_iterint, default=500

Número máximo de iteraciones a realizar. Se puede utilizar para una parada anticipada.

epsfloat, default=np.finfo(float).eps

La regularización de máquina-precisión en el cálculo de los factores diagonales de Cholesky. Aumenta este parámetro para sistemas muy mal condicionados. A diferencia del parámetro tol en algunos algoritmos basados en la optimización iterativa, este parámetro no controla la tolerancia de la optimización.

copy_Xbool, default=True

Si es True, X se copiará; si no, puede ser sobrescrito.

positivebool, default=False

Restringe los coeficientes para que sean >= 0. Ten en cuenta que tal vez quieras eliminar fit_intercept que está establecido True por defecto. Bajo la restricción positiva los coeficientes del modelo no convergen a la solución de mínimos cuadrados ordinarios para valores pequeños de alfa. Sólo los coeficientes hasta el valor más pequeño de alfa (alphas_[alphas_ > 0.].min() cuando fit_path=True) alcanzados por el algoritmo de Lars-Lasso por pasos están típicamente en congruencia con la solución del estimador Lasso de descenso coordinado. En consecuencia, utilizar LassoLarsIC sólo tiene sentido para los problemas en los que se espera y/o se alcanza una solución dispersa.

Atributos

coef_array-like de forma (n_features,)

vector de parámetros (w en la fórmula de formulación)

intercept_float

término independiente en la función de decisión.

alpha_float

el parámetro alfa elegido por el criterio de información

alphas_array-like de forma (n_alphas + 1,) o lista de ese tipo de arreglos

Máximo de covarianzas (en valor absoluto) en cada iteración. n_alphas es max_iter, n_features o el número de nodos en el camino con alpha >= alpha_min, el que sea menor. Si es una lista (list), será de longitud n_targets.

n_iter_int

número de iteraciones ejecutadas por lars_path para encontrar la cuadrícula de alfas.

criterion_array-like de forma (n_alphas,)

El valor de los criterios de información (“aic”, “bic”) en todos los alfas. Se elige el alfa que tiene el menor criterio de información. Este valor es mayor por un factor de n_samples en comparación con las Ecuaciones 2.15 y 2.16 en (Zou et al, 2007).

Ver también

lars_path, LassoLars, LassoLarsCV

Notas

La estimación del número de grados de libertad viene dada por:

«On the degrees of freedom of the lasso» Hui Zou, Trevor Hastie, y Robert Tibshirani Ann. Statist. Volume 35, Number 5 (2007), 2173-2192.

https://en.wikipedia.org/wiki/Akaike_information_criterion https://en.wikipedia.org/wiki/Bayesian_information_criterion

Ejemplos

>>> from sklearn import linear_model
>>> reg = linear_model.LassoLarsIC(criterion='bic')
>>> reg.fit([[-1, 1], [0, 0], [1, 1]], [-1.1111, 0, -1.1111])
LassoLarsIC(criterion='bic')
>>> print(reg.coef_)
[ 0.  -1.11...]

Métodos

fit	Ajusta el modelo utilizando X, y como datos de entrenamiento.
get_params	Obtiene los parámetros para este estimador.
predict	Predice utilizando el modelo lineal.
score	Devuelve el coeficiente de determinación \(R^2\) de la predicción.
set_params	Establece los parámetros de este estimador.

fit()

Ajusta el modelo utilizando X, y como datos de entrenamiento.

Parámetros

Xarray-like de forma (n_samples, n_features)

datos del entrenamiento.

yarray-like de forma (n_samples,)

valores objetivo. Se convertirá al dtype de X si es necesario

copy_Xbool, default=None

Si se proporciona, este parámetro anulará la elección de copy_X realizada en la creación de la instancia. Si es True, X se copiará; de lo contrario, se puede sobrescribir.

Devuelve

selfobject

devuelve una instancia de sí misma.

get_params()

Obtiene los parámetros para este estimador.

Parámetros

deepbool, default=True

Si es True, devolverá los parámetros para este estimador y los subobjetos contenidos que son estimadores.

Devuelve

paramsdict

Los nombres de los parámetros mapeados a sus valores.

predict()

Predice utilizando el modelo lineal.

Parámetros

Xarray-like o matriz dispersa, de forma (n_samples, n_features)

Muestras.

Devuelve

Carreglo, forma (n_samples,)

Devuelve los valores predichos.

score()

Devuelve el coeficiente de determinación \(R^2\) de la predicción.

El coeficiente \(R^2\) se define como \((1 - \frac{u}{v})\), donde \(u\) es la suma de cuadrados de los residuos ((y_true - y_pred) ** 2).sum() y \(v\) es la suma de cuadrados total ((y_true - y_true.mean()) ** 2).sum(). La mejor puntuación posible es 1.0 y puede ser negativa (porque el modelo puede ser arbitrariamente peor). Un modelo constante que siempre predice el valor esperado de y, sin tener en cuenta las características de entrada, obtendría una puntuación \(R^2\) de 0.0.

Parámetros

Xarray-like de forma (n_samples, n_features)

Muestras de prueba. Para algunos estimadores puede ser una matriz núcleo precalculada o una lista de objetos genéricos con forma (n_samples, n_samples_fitted), donde n_samples_fitted es el número de muestras utilizadas en el ajuste para el estimador.

yarray-like de forma (n_samples,) o (n_samples, n_outputs)

Valores verdaderos para X.

sample_weightarray-like de forma (n_samples,), default=None

Ponderaciones de la muestra.

Devuelve

scorefloat

\(R^2\) de self.predict(X) con respecto a y.

Notas

La puntuación \(R^2\) utilizada al invocar a score en un regresor utiliza multioutput='uniform_average' desde la versión 0.23 para mantener la consistencia con el valor predeterminado de r2_score. Esto influye en el método score de todos los regresores de salida múltiple (excepto para MultiOutputRegressor).

set_params()

Establece los parámetros de este estimador.

El método funciona tanto en estimadores simples como en objetos anidados (como Pipeline). Estos últimos tienen parámetros de la forma <component>__<parameter> para que sea posible actualizar cada componente de un objeto anidado.

Parámetros

**paramsdict

Parámetros del estimador.

Devuelve

selfinstancia de estimador

Instancia del estimador.

Ejemplos utilizando sklearn.linear_model.LassoLarsIC

Selección del modelo Lasso: Validación cruzada / AIC / BIC