Graficar los coeficientes de Ridge en función de la regularización

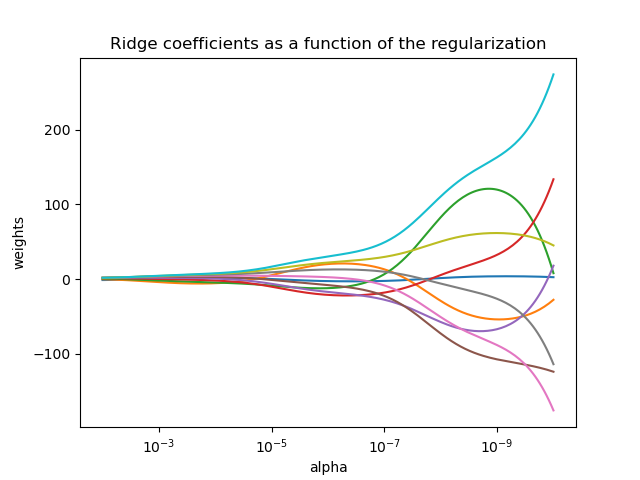
Muestra el efecto de la colinealidad en los coeficientes de un estimador.

Ridge Regresión es el estimador utilizado en este ejemplo. Cada color representa una característica diferente del vector de coeficientes, y esto se muestra en función del parámetro de regularización.

Este ejemplo también muestra la utilidad de aplicar la regresión Ridge a matrices muy mal condicionadas. En este tipo de matrices, un ligero cambio en la variable objetivo puede provocar enormes variaciones en los pesos calculados. En estos casos, es útil establecer una determinada regularización (alfa) para reducir esta variación (ruido).

Cuando alfa es muy grande, el efecto de regularización domina la función de pérdida al cuadrado y los coeficientes tienden a cero. Al final del camino, cuando alfa tiende a cero y la solución tiende a los mínimos cuadrados ordinarios, los coeficientes presentan grandes oscilaciones. En la práctica, es necesario afinar alfa de forma que se mantenga un equilibrio entre ambos.

# Author: Fabian Pedregosa -- <fabian.pedregosa@inria.fr>
# License: BSD 3 clause

print(__doc__)

import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model

# X is the 10x10 Hilbert matrix
X = 1. / (np.arange(1, 11) + np.arange(0, 10)[:, np.newaxis])
y = np.ones(10)

# #############################################################################
# Compute paths

n_alphas = 200
alphas = np.logspace(-10, -2, n_alphas)

coefs = []
for a in alphas:
    ridge = linear_model.Ridge(alpha=a, fit_intercept=False)
    ridge.fit(X, y)
    coefs.append(ridge.coef_)

# #############################################################################
# Display results

ax = plt.gca()

ax.plot(alphas, coefs)
ax.set_xscale('log')
ax.set_xlim(ax.get_xlim()[::-1])  # reverse axis
plt.xlabel('alpha')
plt.ylabel('weights')
plt.title('Ridge coefficients as a function of the regularization')
plt.axis('tight')
plt.show()