Regresión logística dispersa multiclase en 20 nuevos grupos

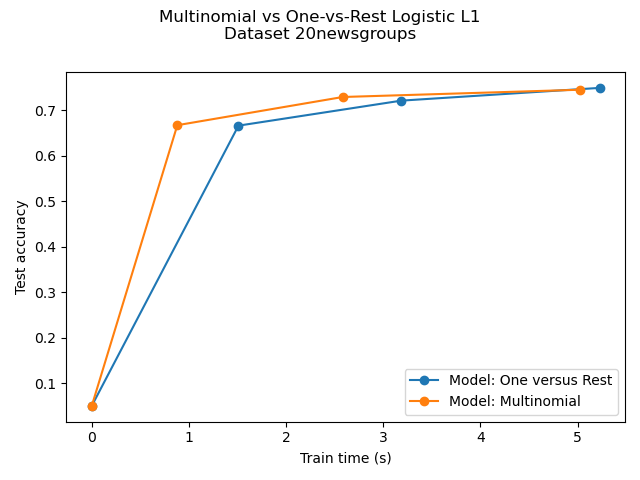
Comparación de la regresión logística multinomial L1 frente a la regresión logística L1 de uno contra uno para clasificar documentos del conjunto de datos newgroups20. La regresión logística multinomial arroja resultados más precisos y es más rápida de entrenar en el conjunto de datos de mayor escala.

Aquí utilizamos la dispersión l1 que recorta los pesos de las características no informativas a cero. Esto es bueno si el objetivo es extraer el vocabulario fuertemente discriminativo de cada clase. Si el objetivo es obtener la mejor exactitud predictiva, es mejor utilizar la penalización l2 que no induce a la dispersión.

Una forma más tradicional (y posiblemente mejor) de predecir sobre un subconjunto disperso de características de entrada sería utilizar la selección univariante de características seguida de un modelo de regresión logística tradicional (l2-penalizado).

Out:

Dataset 20newsgroup, train_samples=9000, n_features=130107, n_classes=20
[model=One versus Rest, solver=saga] Number of epochs: 1
[model=One versus Rest, solver=saga] Number of epochs: 2
[model=One versus Rest, solver=saga] Number of epochs: 4
Test accuracy for model ovr: 0.7490
% non-zero coefficients for model ovr, per class:
 [0.31743104 0.36815852 0.4181174  0.46115889 0.24595141 0.41350581
 0.31281945 0.27054655 0.58720899 0.32972861 0.4158116  0.3312658
 0.41888599 0.41120001 0.59643217 0.31666244 0.34279478 0.28130692
 0.35278655 0.24748861]
Run time (4 epochs) for model ovr:5.23
[model=Multinomial, solver=saga] Number of epochs: 1
[model=Multinomial, solver=saga] Number of epochs: 3
[model=Multinomial, solver=saga] Number of epochs: 7
Test accuracy for model multinomial: 0.7450
% non-zero coefficients for model multinomial, per class:
 [0.13219888 0.11452112 0.13066169 0.13681047 0.12066991 0.15909982
 0.13450468 0.09146318 0.07916561 0.12143851 0.13911627 0.10760374
 0.18984374 0.12143851 0.17524038 0.22289346 0.11605832 0.07916561
 0.07301682 0.15141384]
Run time (7 epochs) for model multinomial:5.03
Example run in 19.642 s

import timeit
import warnings

import matplotlib.pyplot as plt
import numpy as np

from sklearn.datasets import fetch_20newsgroups_vectorized
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.exceptions import ConvergenceWarning

print(__doc__)
# Author: Arthur Mensch

warnings.filterwarnings("ignore", category=ConvergenceWarning,
                        module="sklearn")
t0 = timeit.default_timer()

# We use SAGA solver
solver = 'saga'

# Turn down for faster run time
n_samples = 10000

X, y = fetch_20newsgroups_vectorized(subset='all', return_X_y=True)
X = X[:n_samples]
y = y[:n_samples]

X_train, X_test, y_train, y_test = train_test_split(X, y,
                                                    random_state=42,
                                                    stratify=y,
                                                    test_size=0.1)
train_samples, n_features = X_train.shape
n_classes = np.unique(y).shape[0]

print('Dataset 20newsgroup, train_samples=%i, n_features=%i, n_classes=%i'
      % (train_samples, n_features, n_classes))

models = {'ovr': {'name': 'One versus Rest', 'iters': [1, 2, 4]},
          'multinomial': {'name': 'Multinomial', 'iters': [1, 3, 7]}}

for model in models:
    # Add initial chance-level values for plotting purpose
    accuracies = [1 / n_classes]
    times = [0]
    densities = [1]

    model_params = models[model]

    # Small number of epochs for fast runtime
    for this_max_iter in model_params['iters']:
        print('[model=%s, solver=%s] Number of epochs: %s' %
              (model_params['name'], solver, this_max_iter))
        lr = LogisticRegression(solver=solver,
                                multi_class=model,
                                penalty='l1',
                                max_iter=this_max_iter,
                                random_state=42,
                                )
        t1 = timeit.default_timer()
        lr.fit(X_train, y_train)
        train_time = timeit.default_timer() - t1

        y_pred = lr.predict(X_test)
        accuracy = np.sum(y_pred == y_test) / y_test.shape[0]
        density = np.mean(lr.coef_ != 0, axis=1) * 100
        accuracies.append(accuracy)
        densities.append(density)
        times.append(train_time)
    models[model]['times'] = times
    models[model]['densities'] = densities
    models[model]['accuracies'] = accuracies
    print('Test accuracy for model %s: %.4f' % (model, accuracies[-1]))
    print('%% non-zero coefficients for model %s, '
          'per class:\n %s' % (model, densities[-1]))
    print('Run time (%i epochs) for model %s:'
          '%.2f' % (model_params['iters'][-1], model, times[-1]))

fig = plt.figure()
ax = fig.add_subplot(111)

for model in models:
    name = models[model]['name']
    times = models[model]['times']
    accuracies = models[model]['accuracies']
    ax.plot(times, accuracies, marker='o',
            label='Model: %s' % name)
    ax.set_xlabel('Train time (s)')
    ax.set_ylabel('Test accuracy')
ax.legend()
fig.suptitle('Multinomial vs One-vs-Rest Logistic L1\n'
             'Dataset %s' % '20newsgroups')
fig.tight_layout()
fig.subplots_adjust(top=0.85)
run_time = timeit.default_timer() - t0
print('Example run in %.3f s' % run_time)
plt.show()