1.2. Análisis Discriminante Lineal y Cuadrático

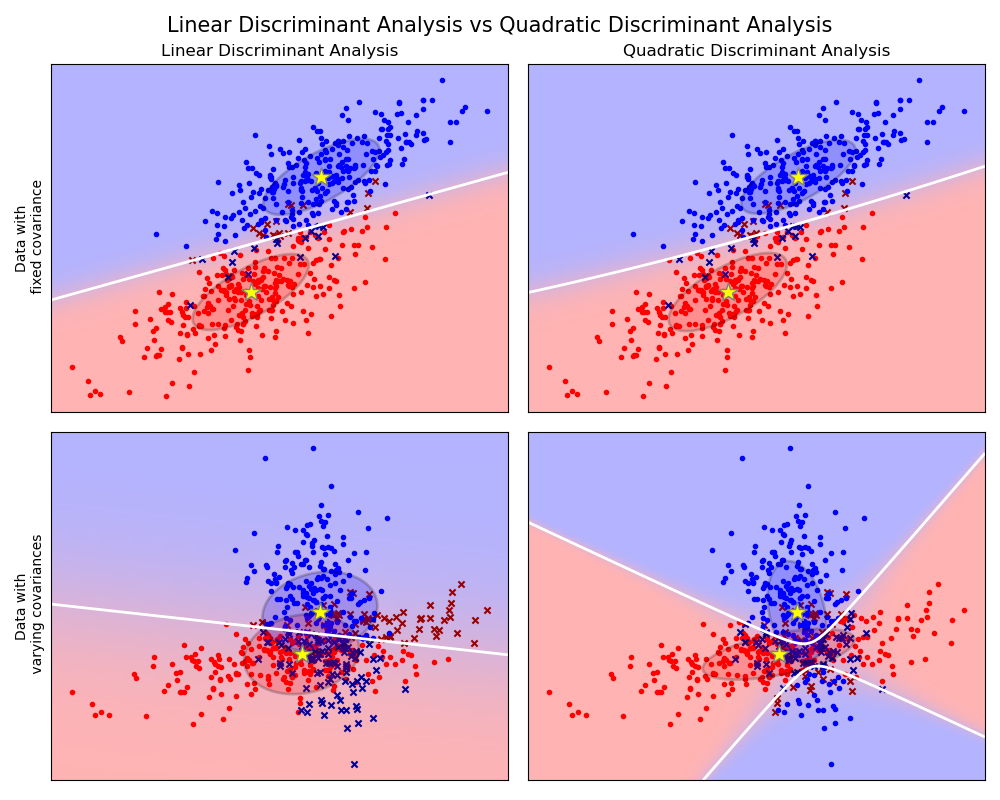
El análisis lineal de discriminantes (LinearDiscriminantAnalysis) y el análisis discriminante cuadrático (QuadraticDiscriminantAnalysis) son dos clasificadores clásicos que tienen, como su nombre lo indica, una superficie de decisión lineal y cuadrática, respectivamente.

Estos clasificadores son atractivos porque tienen soluciones de forma cerrada que pueden ser calculadas fácilmente, son inherentemente multiclase, se ha demostrado que funcionan bien en la practica, y no tienen hiperparámetros que ajustar.

El gráfico muestra los límites de decisión para el Análisis Discriminante Lineal y el Análisis Discriminante Cuadrático. La fila de abajo demuestra que el Análisis Discriminante Lineal solo puede aprender límites lineales, mientras que el Análisis Discriminante Cuadrático puede aprender límites cuadráticos y es por lo tanto mas flexible.

Ejemplos:

Análisis discriminante lineal y cuadrático con elipsoide de covarianza: Comparación de ADL y ADQ en datos sintéticos.

1.2.1. Reducción de dimensionalidad usando el Análisis Discriminante Lineal

El LinearDiscriminantAnalysis puede ser utilizado para realizar una reducción de dimensionalidad supervisada, mediante la proyección de los datos de entrada a un subespacio lineal consistiendo de las direcciones que maximizen la separación entre las clases (en un sentido preciso discutido en la sección de matemáticas abajo). La dimensión de la salida es necesariamente menor que el número de las clases, por lo que esto es en general una reducción de dimensionalidad bastante fuerte, y solo tiene sentido en un ajustamiento multiclase.

Esto está implementado en el método transform. La dimensionalidad deseada puede establecerse usando el parámetro n_components. Este parámetro no tiene influencia en los métodos fit y predict.

Ejemplos:

Comparación de la proyección arreglo 2D de LDA y PCA del conjunto de datos de Iris: Comparación de ADL y PCA para la reducción de dimensionalidad del conjunto de datos Iris

1.2.2. Formulación matemática de los clasificadores ADL y ADQ

Tanto ADL como ADQ pueden ser derivados de modelos probabilísticos sencillos que modelan la distribución condicionada por la clase de los datos \(P(X|y=k)\) por cada clase \(k\). Las predicciones pueden entonces ser obtenidas usando la regla de Bayes, para cada muestra de entrenamiento \(x \in \mathcal{R}^d\):

\[P(y=k | x) = \frac{P(x | y=k) P(y=k)}{P(x)} = \frac{P(x | y=k) P(y = k)}{ \sum_{l} P(x | y=l) \cdot P(y=l)}\]

y seleccionamos la clase \(k\) que maximiza esta probabilidad posterior.

Más específicamente, para el análisis discriminante lineal y cuadrático, \(P(x|y)\) está modelado como una distribución Gaussiana multivariante con densidad:

\[P(x | y=k) = \frac{1}{(2\pi)^{d/2} |\Sigma_k|^{1/2}}\exp\left(-\frac{1}{2} (x-\mu_k)^t \Sigma_k^{-1} (x-\mu_k)\right)\]

donde \(d\) es el número de características.

1.2.2.1. ADQ

De acuerdo con el modelo anterior, el log del posterior es:

\[\begin{split}\log P(y=k | x) &= \log P(x | y=k) + \log P(y = k) + Cst \\ &= -\frac{1}{2} \log |\Sigma_k| -\frac{1}{2} (x-\mu_k)^t \Sigma_k^{-1} (x-\mu_k) + \log P(y = k) + Cst,\end{split}\]

donde el termino constante \(Cst\) corresponde al denominador \(P(x)\), junto a los otros terminos constantes del Gaussiano. La clase predicha es aquella que maximiza este log-posterior.

Nota

Relación con Bayes ingenuo Gaussiano

Si en el modelo ADQ uno asumo que las matrices de covarianza son diagonales, entonces se asume que las entradas son condicionalmente independientes en cada clase, y que el clasificador resultante es equivalente al clasificador Bayesiano Ingenuo Gaussiano naive_bayes.GaussianNB.

1.2.2.2. ADL

El ADL es un caso especial de ADQ, donde se asume que los Gaussianos de cada clase comparten la misma matriz de covarianza: \(\Sigma_k = \Sigma\) para todo \(k\). Esto reduce el log posterior a:

\[\log P(y=k | x) = -\frac{1}{2} (x-\mu_k)^t \Sigma^{-1} (x-\mu_k) + \log P(y = k) + Cst.\]

El termino \((x-\mu_k)^t \Sigma^{-1} (x-\mu_k)\) corresponde a la Distancia de Mahalanobis <https://es.wikipedia.org/wiki/Distancia_de_Mahalanobis>`_ desde la muestra \(x\) y la media \(\mu_k\). La distancia de Mahalanobis nos dice que tan cerca esta \(x\) desde \(\mu_k\), mientras que se toma en cuenta la varianza de cada característica. Podemos entonces interpretar al ADL como asignar \(x\) a aquella clase cuya media es la mas cercana en terminos de distancia de Mahalanobis, mientras también se contabilizan las probabilidades previas de la clase.

El log-posterior de ADL también se puede escribir 3 como:

\[\log P(y=k | x) = \omega_k^t x + \omega_{k0} + Cst.\]

donde \(\omega_k = \Sigma^{-1} \mu_k\) y \(\omega_{k0} = -\frac{1}{2} \mu_k^t\Sigma^{-1}\mu_k + \log P (y = k)\). Estas cantidades corresponden a los atributos coef_ y intercept_, respectivamente.

De la fórmula anterior, está claro que el ADL tiene una superficie de decisión lineal. En el caso del ADQ, no hay suposiciones sobre las matrices de covarianza \(\Sigma_k\) de los gaussianos, lo que lleva a superficies cuadráticas de decisión. Ver 1 para más detalles.

1.2.3. Formulación matemática de la reducción de dimensionalidad del ADL

Primero nota que la K significa que \(\mu_k\) son vectores en \(\mathcal{R}^d\), y que se encuentran en un subespacio afín \(H\) de dimensión al menos \(K - 1\) (2 puntos yacen en una linea, 3 points en un plano, etc).

Como se mencionó anteriormente, podemos interpretar ADL como asignar \(x\) a la clase cuya media \(\mu_k\) es la mas cercana en terminos de distancia de Mahalanobis, también contabilizando por las probabilidades previas de la clase. Alternativamente, LDA es equivalente a primero esferificar los datos para que la matriz de covarianza sea la identidad, luego asignando \(x\) a la media mas cercana en terminos de distancia Euclidiana (igualmente tomando en cuenta las previas clases).

Calcular distancias Euclídeas en este espacio d-dimensional es equivalente a primero proyectar los puntos de datos en \(H\), y calcular las distancias ahí (ya que las otras dimensiones van a contribuir de manera igual a cada clase en termínos de distancia). En otras palabras, si \(k\) es el mas cercano a \(\mu_k\) en el espacio original, también sera el caso en \(H\). Esto nos muestra que hay una reducción de dimensionalidad por proyección lineal hacía un espacio de \(K-1\) dimensiones implícita en el clasificador ADL.

Podemos reducir la dimensión aún mas, a un \(L\) elegido, si proyectamos hacia el subespacio lineal \(H_L\) que maximiza la varianza de \(\mu^*_k\) después de la proyección (en efecto, estamos haciendo una forma de PCA para las medias de clase transformadas \(\mu^*_k\)). Este \(L\) corresponde al parámetro n_components usado en el método transform. Ver 1 para más detalles.

1.2.4. Estimador de Reducción y Covarianza

La contracción (shrinkage) es una forma de regularización usada para mejorar la estimación de matrices de covarianza en situaciones donde el número de muestras de entrenamiento es pequeño comparado al número de características. En este escenario, la covarianza muestral empírica es un estimador pobre, y la reducción ayuda a mejorar el rendimiento de generalización del clasificador. El ADL de reducción se puede utilizar estableciendo el parámetro shrinkage de la clase LinearDiscriminantAnalysis como “auto”. Esto automáticamente determina que el parámetro óptimo de reducción siguiendo el lemma introducido por Ledoit y Wolf 2. Note que por el momento la reducción solo funciona cuando el parámetro solver esta configurado como “lsqr” o “eigen”.

El parámetro shrinkage también puede establecerse manualmente entre 0 y 1. En particular, un valor de 0 corresponde a ninguna reducción (lo cual significa que la matriz de covarianza empírica sera utilizada), y un valor de 1 corresponde a reducción total (lo cual significa que la matriz diagonal de varianzas sera utilizada como un estimado para la matriz de covarianza). Si se pasa un valor entre estos dos extremos a este parámetro, se estimara una versión reducida del matriz de covarianza.

El estimador de covarianza Ledoit y Wolf reducido quizás no sea siempre la mejor opción. Por ejemplo, si la distribución de lo datos esta normalmente distribuida, el estimador Oracle Shrinkage Approximating sklearn.covariance.OAS da un menor error cuadrático medio que el dado por la formula de Ledoit y Wolf usada con shrinkage=»auto». En ADL, los datos se presumen que son condicionalmente gaussianos a la clase. Si estos supuestos se cumplen, usar ADL con el estimador de covarianza OAS dará una mejor precisión de clasificación que si se usan los estimadores Lediot y Wolf o de covarianza empírica.

El estimador de covarianza se puede escoger utilizando el parámetro covariance_estimator de la clase discriminant_analysis.LinearDiscriminantAnalysis. Un estimador de covarianza debería tener un método fit y un atributo covariance_ como todos los estimadores de covarianza en el módulo sklearn.covariance.

reducción

Ejemplos:

Análisis discriminante lineal normal, Ledoit-Wolf y OAS para la clasificación: Comparación de los clasificadores ADL con los estimadores de covarianza Empíricos, Ledoit Wolf y OAS.

1.2.5. Algoritmos de estimación

Usar ADL y ADQ requiere calcular el log-posterior que depende en los antecedentes de clase \(P(y=k)\), los medios de clase \(\mu_k\) y las matrices de covarianza.

El solucionador “svd” es el solucionador por defecto utilizado por LinearDiscriminantAnalysis, y es el único solucionador disponible para QuadraticDiscriminantAnalysis. Puede realizar tanto clasificación como transformación (para ADL). Ya que no se basa en el cálculo de la matriz de covarianza, el solucionador “svd” podría ser preferible en situaciones donde el número de características es grande. El solucionador “svd” no puede ser utilizado con reducción. Para el ADQ, el uso del solucionador SVD se sostiene en el hecho de que la matriz de covarianza \(\Sigma_k\) es, por definición, igual a \(\frac{1}{n - 1} X_k^tX_k = V S^2 V^t\), donde \(V\) viene del SVD de la matriz (centrada): \(X_k = U S V^t\). Resulta que podemos calcular el log-posterior anterior sin necesitar calcular explícitamente \(\Sigma\): calcular \(S\) y \(V\) mediante el SVD de \(X\) es suficiente. Para el ADL, se calculan dos SVD: el SVD de la matriz de entrada centrada \(X\) y el SVD de los vectores medios por clase.

El solucionador “lsqr” es un algoritmo eficiente que sólo funciona para la clasificación. Necesita calcular explicitamente la covarianza de matriz \(\Sigma\), y soporta estimadores de reducción y covarianza personalizada. Este solucionador calcula los coeficientes \(\omega_k = \Sigma^{-1}\mu_k\) resolviendo \(\Sigma \omega = \mu_k\), así evitando el calculo explicito de la inversa \(\Sigma^{-1}\).

El solucionador “eigen” está basado en la optimización de la razón entre la dispersión entre clases y la dispersión dentro de clases. Puede ser utilizada tanto para clasificación como transformación, y soporta la reducción. Sin embargo, el solucionador “eigen” necesita calcular la matriz de covarianza, así que quizás no sea adecuado para situaciones con un gran número de características.

Referencias:

1(1,2)

«The Elements of Statistical Learning», Hastie T., Tibshirani R., Friedman J., Section 4.3, p.106-119, 2008.

2

Ledoit O, Wolf M. Honey, I Shrunk the Sample Covariance Matrix. The Journal of Portfolio Management 30(4), 110-119, 2004.

3

R. O. Duda, P. E. Hart, D. G. Stork. Pattern Classification (Second Edition), section 2.6.2.