1.3. Regresión de cresta de núcleo

La regresión de cresta del núcleo (Kernel Ridge Regression, KRR) [M2012] combina Regresión de cresta y clasificación (mínimos cuadrados lineales con regularización de la norma l2) con el kernel triciclo. Así aprende una función lineal en el espacio inducido por el núcleo respectivo y los datos. Para los núcleos no lineales, esto corresponde a una función no lineal en el espacio original.

La forma del modelo aprendido por KernelRidge es idéntica a la regresión de vectores de soporte (SVR). Sin embargo, se utilizan diferentes funciones de pérdida: KRR utiliza la pérdida de error al cuadrado mientras que la regresión de vectores de soporte utiliza la pérdida insensible (insensitive loss) a \(\epsilon\), ambas combinadas con la regularización l2. A diferencia de SVR, el ajuste de KernelRidge puede realizarse de forma cerrada y suele ser más rápido para conjuntos de datos de tamaño medio. Por otro lado, el modelo aprendido no es disperso y por lo tanto es más lento que SVR, que aprende un modelo disperso para \(\epsilon > 0\), en tiempo de predicción.

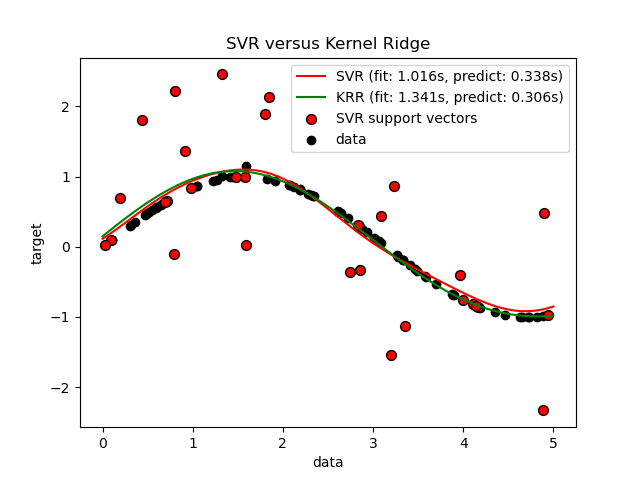
La siguiente figura compara KernelRidge y SVR en un conjunto de datos artificial, que consiste en una función objetivo sinusoidal y un fuerte ruido añadido cada quinto punto de datos. El modelo aprendido de KernelRidge y SVR se representa gráficamente, donde tanto la complejidad/regularización como el ancho de banda del kernel RBF se han optimizado utilizando la búsqueda en cuadrícula (grid-search). Las funciones aprendidas son muy similares; sin embargo, el ajuste de KernelRidge es aproximadamente siete veces más rápido que el ajuste de SVR (ambos con búsqueda en cuadrícula). Sin embargo, la predicción de 100.000 valores objetivo es más de tres veces más rápida con SVR ya que ha aprendido un modelo disperso utilizando sólo aproximadamente 1/3 de los 100 puntos de datos de entrenamiento como vectores de soporte.

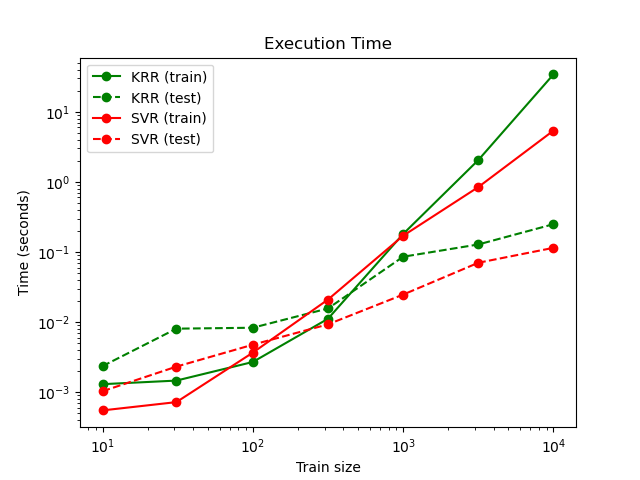
La siguiente figura compara el tiempo de ajuste y predicción de KernelRidge y SVR para diferentes tamaños del conjunto de entrenamiento. El ajuste de KernelRidge es más rápido que el de SVR para conjuntos de entrenamiento de tamaño medio (menos de 1000 muestras); sin embargo, para conjuntos de entrenamiento más grandes SVR se adapta mejor. Con respecto al tiempo de predicción, SVR es más rápido que KernelRidge para todos los tamaños del conjunto de entrenamiento debido a la solución dispersa aprendida. Ten en cuenta que el grado de dispersión y por lo tanto el tiempo de predicción depende de los parámetros \(\epsilon\) y \(C\) de la SVR; \(\epsilon = 0\) correspondería a un modelo denso.

Referencias:

M2012

«Machine Learning: A Probabilistic Perspective» Murphy, K. P. - capítulo 14.4.3, pp. 492-493, The MIT Press, 2012