1.4. Máquinas de Vectores de Soporte¶

Las máquinas de vectores de soporte (support vector machines, SVMs) son un conjunto de métodos de aprendizaje supervisado que se utilizan para la clasificación, la regresión y la detección de valores atípicos.

Las ventajas de las máquinas de vectores de soporte son:

Efectivas en espacios de alta dimensión.

Aún efectivas en los casos en que el número de dimensiones es mayor que el número de muestras.

Utilizan un subconjunto de puntos de entrenamiento en la función de decisión (llamados vectores de soporte), por lo que también son eficientes en cuanto a memoria.

Versátiles: se pueden especificar diferentes Funciones del núcleo para la función de decisión. Se proporcionan kernels comunes, pero también es posible especificar núcleos personalizados.

Las desventajas de las máquinas de vectores de soporte incluyen:

Si el número de características es mucho mayor que el número de muestras, hay que evitar el sobreajuste al elegir Funciones del núcleo y el término de regularización es crucial.

Las SVMs no proporcionan directamente estimaciones de probabilidad, éstas se calculan utilizando una costosa validación cruzada de cinco-pliegues (ver Puntuaciones y probabilidades, más abajo).

Las máquinas de vectores de soporte en scikit-learn admiten como entrada tanto vectores de muestra densos (numpy.ndarray y convertibles a eso por numpy.asarray) como dispersos (cualquier scipy.sparse). Sin embargo, para utilizar una SVM para hacer predicciones para datos dispersos, debe haber sido ajustada en dichos datos. Para un rendimiento óptimo, utiliza numpy.ndarray ordenado en C (denso) o scipy.sparse.csr_matrix (disperso) con dtype=float64.

1.4.1. Clasificación¶

SVC, NuSVC y LinearSVC son clases capaces de realizar una clasificación binaria y multiclase en un conjunto de datos.

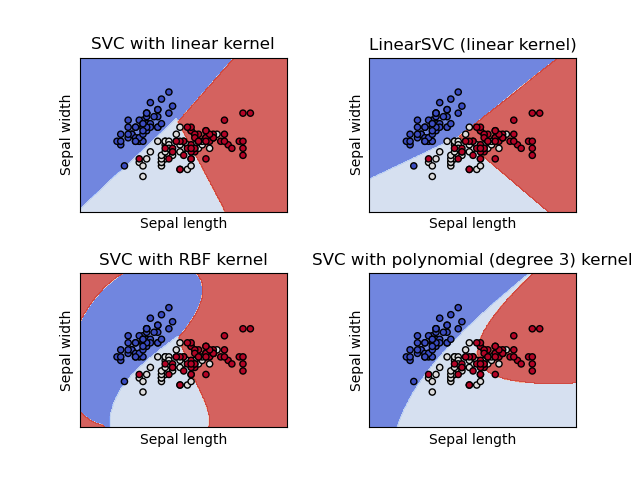
../_images/sphx_glr_plot_iris_svc_001.png

SVC y NuSVC son métodos similares, pero aceptan conjuntos de parámetros ligeramente diferentes y tienen formulaciones matemáticas distintas (ver la sección Formulación matemática). Por otro lado, LinearSVC es otra implementación (más rápida) de la Clasificación por Vectores de Soporte para el caso de un núcleo lineal. Ten en cuenta que LinearSVC no acepta el parámetro kernel, ya que se supone que es lineal. También carece de algunos de los atributos de SVC y NuSVC, como support_.

Como otros clasificadores, SVC, NuSVC y LinearSVC toman como entrada dos arreglos: un arreglo X de forma (n_samples, n_features) que contiene las muestras de entrenamiento, y un arreglo y de etiquetas de clase (cadenas o enteros), de forma (n_samples):

>>> from sklearn import svm
>>> X = [[0, 0], [1, 1]]
>>> y = [0, 1]
>>> clf = svm.SVC()
>>> clf.fit(X, y)
SVC()

Una vez ajustado, el modelo puede ser utilizado para predecir nuevos valores:

>>> clf.predict([[2., 2.]])
array([1])

La función de decisión de las SVMs (detallada en la Formulación matemática) depende de un subconjunto de los datos de entrenamiento, llamados vectores de soporte. Algunas propiedades de estos vectores de soporte se pueden encontrar en los atributos support_vectors_, support_ y n_support_:

>>> # get support vectors
>>> clf.support_vectors_
array([[0., 0.],
       [1., 1.]])
>>> # get indices of support vectors
>>> clf.support_
array([0, 1]...)
>>> # get number of support vectors for each class
>>> clf.n_support_
array([1, 1]...)

Ejemplos:

1.4.1.1. Clasificación multiclase¶

SVC y NuSVC implementan el enfoque «uno contra uno» para la clasificación multiclase. En total, se construyen n_classes * (n_classes - 1) / 2` clasificadores y cada uno entrena datos de dos clases. Para proporcionar una interfaz consistente con otros clasificadores, la opción ``decision_function_shape permite transformar monotónicamente los resultados de los clasificadores «uno contra uno» a una función de decisión «uno contra el resto» de forma (n_samples, n_classes).

>>> X = [[0], [1], [2], [3]]
>>> Y = [0, 1, 2, 3]
>>> clf = svm.SVC(decision_function_shape='ovo')
>>> clf.fit(X, Y)
SVC(decision_function_shape='ovo')
>>> dec = clf.decision_function([[1]])
>>> dec.shape[1] # 4 classes: 4*3/2 = 6
6
>>> clf.decision_function_shape = "ovr"
>>> dec = clf.decision_function([[1]])
>>> dec.shape[1] # 4 classes
4

Por otro lado, LinearSVC implementa la estrategia multiclase «uno contra el resto», entrenando así modelos n_classes.

>>> lin_clf = svm.LinearSVC()
>>> lin_clf.fit(X, Y)
LinearSVC()
>>> dec = lin_clf.decision_function([[1]])
>>> dec.shape[1]
4

Ver Formulación matemática para una descripción completa de la función de decisión.

Ten en cuenta que LinearSVC también implementa una estrategia alternativa multiclase, la llamada SVM multiclase formulada por Crammer y Singer 16, utilizando la opción multi_class='crammer_singer'. En la práctica, se suele preferir la clasificación uno contra el resto, ya que los resultados son en su mayoría similares, pero el tiempo de ejecución es significativamente menor.

Para el LinearSVC «uno contra el resto» los atributos coef_ e intercept_ tienen la forma (n_classes, n_features) y (n_classes,) respectivamente. Cada fila de los coeficientes corresponde a uno de los clasificadores n_classes «uno contra el resto» y lo mismo para los interceptos, en el orden de la clase «uno».

En el caso de SVC y NuSVC «uno contra uno», la disposición de los atributos es un poco más complicada. En el caso de un núcleo lineal, los atributos coef_ e intercept_ tienen la forma (n_classes * (n_classes - 1) / 2, n_features) y (n_classes * (n_classes - 1) / 2) respectivamente. Esto es similar al diseño de LinearSVC descrito anteriormente, con cada fila correspondiente a un clasificador binario. El orden para las clases 0 a n es «0 vs 1», «0 vs 2», … «0 vs n», «1 vs 2», «1 vs 3», «1 vs n», … «n-1 vs n».

La forma de dual_coef_ es (n_classes-1, n_SV) con un diseño algo difícil de entender. Las columnas corresponden a los vectores de soporte implicados en cualquiera de los n_classes * (n_classes - 1) / 2 clasificadores «uno contra uno». Cada uno de los vectores de soporte se utiliza en n_classes - 1 clasificadores. Las n_classes - 1 entradas de cada fila corresponden a los coeficientes duales para estos clasificadores.

Esto puede ser más claro con un ejemplo: considera un problema de tres clases con la clase 0 que tiene tres vectores de soporte \(v^{0}_0, v^{1}_0, v^{2}_0\) y las clases 1 y 2 que tienen dos vectores de soporte \(v^{0}_1, v^{1}_1\) y \(v^{0}_2, v^{1}_2\) respectivamente. Para cada vector de soporte \(v^{j}_i\), hay dos coeficientes duales. Llamemos al coeficiente del vector de soporte \(v^{j}_i\) en el clasificador entre las clases \(i\) y \(k\) \(alpha^{j}_{i,k}\). Entonces dual_coef_ tiene el siguiente aspecto:

\(\alpha^{0}_{0,1}\)	\(\alpha^{0}_{0,2}\)	Coeficientes para SVs de la clase 0
\(\alpha^{1}_{0,1}\)	\(\alpha^{1}_{0,2}\)
\(\alpha^{2}_{0,1}\)	\(\alpha^{2}_{0,2}\)
\(\alpha^{0}_{1,0}\)	\(\alpha^{0}_{1,2}\)	Coeficientes para SVs de la clase 1
\(\alpha^{1}_{1,0}\)	\(\alpha^{1}_{1,2}\)	Coeficientes para SVs de la clase 1
\(\alpha^{0}_{2,0}\)	\(\alpha^{0}_{2,1}\)	Coeficientes para SVs de la clase 2
\(\alpha^{1}_{2,0}\)	\(\alpha^{1}_{2,1}\)	Coeficientes para SVs de la clase 2

Ejemplos:

Traza diferentes clasificadores SVM en el conjunto de datos iris,

1.4.1.2. Puntuaciones y probabilidades¶

El método decision_function de SVC y NuSVC proporciona puntuaciones por clase para cada muestra (o una única puntuación por muestra en el caso binario). Cuando la opción del constructor probability` se establece en ``True, se habilitan las estimaciones de probabilidad de pertenencia a la clase (de los métodos predict_proba y predict_log_proba). En el caso binario, las probabilidades se calibran utilizando el escalamiento de Platt 9: regresión logística sobre las puntuaciones de la SVM, ajustada por una validación cruzada adicional sobre los datos de entrenamiento. En el caso multiclase, esto se amplía según 10.

Nota

El mismo procedimiento de calibración de la probabilidad está disponible para todos los estimadores a través de CalibratedClassifierCV (ver Calibración de probabilidad). En el caso de SVC y NuSVC, este procedimiento está incorporado en libsvm que se utiliza a nivel interno, por lo que no depende de CalibratedClassifierCV de scikit-learn.

La validación cruzada que implica el escalamiento de Platt es una operación costosa para conjuntos de datos grandes. Además, las estimaciones de probabilidad pueden ser inconsistentes con las puntuaciones:

el «argmax» de las puntuaciones puede no ser el argmax de las probabilidades
en la clasificación binaria, una muestra puede ser etiquetada por predict como perteneciente a la clase positiva incluso si la salida de predict_proba es menor que 0,5; y de forma similar, podría ser etiquetada como negativa incluso si la salida de predict_proba es mayor que 0,5.

También se sabe que el método de Platt tiene problemas teóricos. Si se requieren puntuaciones de confianza, pero éstas no tienen que ser probabilidades, entonces es aconsejable establecer probability=False y utilizar decision_function en lugar de predict_proba.

Ten en cuenta que cuando decision_function_shape='ovr' y n_classes > 2, a diferencia de decision_function, el método predict no intenta romper vínculos por defecto. Puedes establecer break_ties=True para que la salida de predict sea la misma que np.argmax(clf.decision_function(...), axis=1), de lo contrario siempre se devolverá la primera clase entre las clases vinculadas; pero ten en cuenta que tiene un costo computacional. Ver Ejemplo de desempate SVM para un ejemplo de desvinculación.

1.4.1.3. Problemas no balanceados¶

En los problemas en los que se desea dar más importancia a ciertas clases o a ciertas muestras individuales, se pueden utilizar los parámetros class_weight y sample_weight.

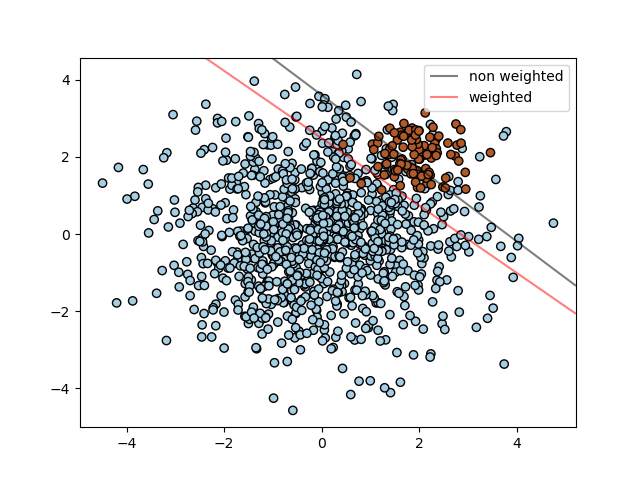
SVC (pero no NuSVC) implementa el parámetro class_weight en el método fit. Es un diccionario de la forma {class_label : value}, donde value es un número de punto flotante > 0 que establece el parámetro C de la clase class_label a C * value. La figura siguiente ilustra la frontera de decisión de un problema no balanceado, con y sin corrección de ponderación.

../_images/sphx_glr_plot_separating_hyperplane_unbalanced_001.png

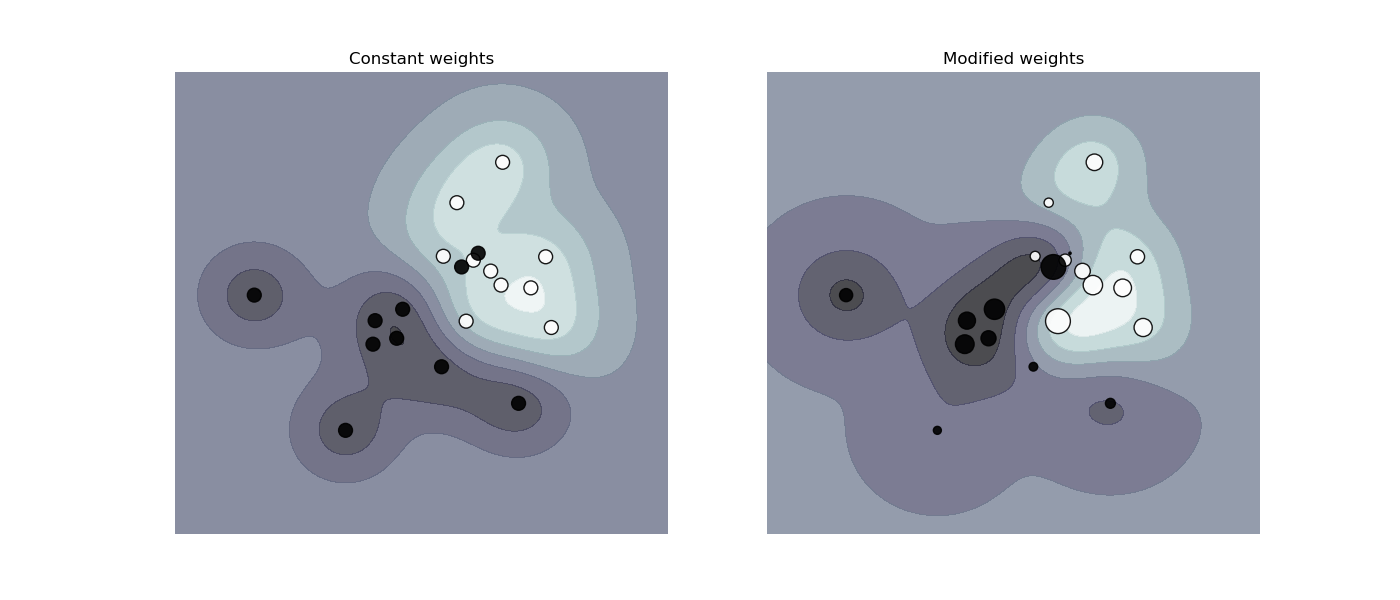
SVC, NuSVC, SVR, NuSVR, LinearSVC, LinearSVR y OneClassSVM implementan también ponderaciones para las muestras individuales en el método fit a través del parámetro sample_weight. Similar a class_weight, establece el parámetro C para el ejemplo i-ésimo en C * sample_weight[i], lo que animará al clasificador a acertar con estas muestras. La figura siguiente ilustra el efecto de la ponderación de las muestras en la frontera de decisión. El tamaño de los círculos es proporcional a las ponderaciones de las muestras:

../_images/sphx_glr_plot_weighted_samples_001.png

Ejemplos:

1.4.2. Regresión¶

El método de Clasificación por Vectores de Soporte puede ampliarse para resolver problemas de regresión. Este método se denomina Regresión con Vectores de Soporte.

El modelo producido por la clasificación por vectores de soporte (como se ha descrito anteriormente) sólo depende de un subconjunto de los datos de entrenamiento, porque la función de costo para construir el modelo no se preocupa por los puntos de entrenamiento que se encuentran más allá del margen. De forma análoga, el modelo producido por la Regresión con Vectores de Soporte depende sólo de un subconjunto de los datos de entrenamiento, porque la función de costo ignora muestras cuya predicción está cerca de su objetivo.

Hay tres implementaciones diferentes de la Regresión con Vectores de Soporte: SVR, NuSVR y LinearSVR. LinearSVR proporciona una implementación más rápida que SVR pero sólo considera el núcleo lineal, mientras que NuSVR implementa una formulación ligeramente diferente a la de SVR y LinearSVR. Ver Detalles de implementación para más detalles.

Al igual que con las clases de clasificación, el método de ajuste tomará como argumento los vectores X, y, sólo que en este caso se espera que y tenga valores de punto flotante en lugar de valores enteros:

>>> from sklearn import svm
>>> X = [[0, 0], [2, 2]]
>>> y = [0.5, 2.5]
>>> regr = svm.SVR()
>>> regr.fit(X, y)
SVR()
>>> regr.predict([[1, 1]])
array([1.5])

Ejemplos:

Soporta la Regresión Vectorial (SVR) usando núcleos lineales y no lineales

1.4.3. Estimación de la densidad, detección de novedades¶

La clase OneClassSVM implementa una SVM de una clase que se utiliza en la detección de valores atípicos.

Ver Detección de novedades y valores atípicos para la descripción y uso de OneClassSVM.

1.4.4. Complejidad¶

Las Máquinas de Vectores de Soporte son herramientas potentes, pero sus requisitos de cálculo y almacenamiento aumentan rápidamente con el número de vectores de entrenamiento. El core de una SVM es un problema de programación cuadrática (QP) que separa los vectores de soporte del resto de los datos de entrenamiento. El solucionador de QP utilizado por la implementación basada en libsvm escala entre \(O(n_{features} \times n_{samples}^2)\) y \(O(n_{features} \times n_{samples}^3)\) dependiendo de la eficiencia con la que se utilice la caché de libsvm en la práctica (depende del conjunto de datos). Si los datos son muy escasos, \(n_{features}\) debe sustituirse por el número promedio de características distintas de cero en un vector de muestras.

Para el caso lineal, el algoritmo utilizado en LinearSVC por la implementación liblinear es mucho más eficiente que su contraparte SVC basada en libsvm y puede escalar casi linealmente a millones de muestras y/o características.

1.4.5. Consejos de Uso Práctico¶

Evitar la copia de datos: Para SVC, SVR, NuSVC y NuSVR, si los datos pasados a ciertos métodos no son contiguos ordenados en C y de doble precisión, serán copiados antes de llamar a la implementación C subyacente. Puedes comprobar si un arreglo numpy dado es contiguo a C inspeccionando su atributo flags.

Para LinearSVC (y LogisticRegression) cualquier entrada pasada como un arreglo de numpy será copiada y convertida a la representación interna de datos dispersos de liblinear (números de punto flotante de doble precisión e índices int32 de componentes distintos de cero). Si quieres ajustar un clasificador lineal a gran escala sin copiar un arreglo numpy denso de doble precisión contiguo a C como entrada, te sugerimos que utilices la clase SGDClassifier en su lugar. La función objetivo puede ser configurada para ser casi la misma que la del modelo LinearSVC.

Tamaño de la caché del kernel: Para SVC, SVR, NuSVC y NuSVR, el tamaño de la caché del núcleo tiene un fuerte impacto en los tiempos de ejecución para problemas mayores. Si tienes suficiente RAM disponible, se recomienda establecer cache_size a un valor mayor que el predeterminado de 200(MB), como 500(MB) o 1000(MB).

Establecer C: C es 1 por defecto y es una opción por defecto razonable. Si tienes muchas observaciones ruidosas, debes disminuirla: la disminución de C corresponde a una mayor regularización.

LinearSVC y LinearSVR son menos sensibles a C cuando se hace grande, y los resultados de la predicción dejan de mejorar a partir de cierto umbral. Mientras que los valores más grandes de C tardarán más tiempo en entrenarse, a veces hasta 10 veces más, como se muestra en 11.
Los algoritmos de Máquinas de Vectores de Soporte no son invariantes a la escala, por lo que es altamente recomendable escalar los datos. Por ejemplo, escala cada atributo del vector de entrada X a [0,1] o [-1,+1], o estandarízalo para que tenga media 0 y varianza 1. Ten en cuenta que el mismo escalamiento debe aplicarse al vector de prueba para obtener resultados significativos. Esto puede hacerse fácilmente utilizando Pipeline:
>>> from sklearn.pipeline import make_pipeline
>>> from sklearn.preprocessing import StandardScaler
>>> from sklearn.svm import SVC

>>> clf = make_pipeline(StandardScaler(), SVC())
Ver la sección Preprocesamiento de los datos para más detalles sobre escalamiento y normalización.
En cuanto al parámetro shrinking, citando 12: Descubrimos que si el número de iteraciones es grande, entonces la reducción (shrinking) puede acortar el tiempo de entrenamiento. Sin embargo, si resolvemos el problema de optimización de forma holgada (por ejemplo, utilizando una gran tolerancia de parada), el código sin utilizar la reducción puede ser mucho más rápido

El parámetro nu en NuSVC/OneClassSVM/NuSVR aproxima la fracción de errores de entrenamiento y vectores de soporte.

En SVC, si los datos están desbalanceados (por ejemplo, muchos positivos y pocos negativos), establece class_weight='balanced' y/o prueba diferentes parámetros de penalización C.

Aleatoriedad de las implementaciones subyacentes: Las implementaciones subyacentes de SVC y NuSVC utilizan un generador de números aleatorios sólo para revolver los datos para la estimación de la probabilidad (cuando probability se establece en True). Esta aleatoriedad se puede controlar con el parámetro random_state. Si probability se establece en False estos estimadores no son aleatorios y random_state no tiene efecto en los resultados. La implementación subyacente de OneClassSVM es similar a las de SVC y NuSVC. Como no se proporciona ninguna estimación de probabilidad para OneClassSVM, no es aleatorio.

La implementación subyacente de LinearSVC utiliza un generador de números aleatorios para seleccionar las características cuando se ajusta el modelo con un descenso de coordenadas dual (es decir, cuando dual se establece en True). Por lo tanto, no es raro tener resultados ligeramente diferentes para los mismos datos de entrada. Si esto ocurre, prueba con un parámetro tol más pequeño. Esta aleatoriedad también se puede controlar con el parámetro random_state. Cuando dual se establece en False la implementación subyacente de LinearSVC no es aleatoria y random_state no tiene efecto en los resultados.

El uso de la penalización L1, tal y como proporciona LinearSVC(penalty='l1', dual=False) produce una solución dispersa, es decir, sólo un subconjunto de ponderaciones de características es diferente de cero y contribuye a la función de decisión. Si se aumenta C se obtiene un modelo más complejo (se seleccionan más características). El valor de C que produce un modelo «nulo» (todas las ponderaciones son iguales a cero) puede calcularse utilizando l1_min_c.

1.4.6. Funciones del núcleo¶

La función del núcleo puede ser cualquiera de las siguientes:

lineal: \(\langle x, x'\rangle\).

polinomial: \((\gamma \langle x, x'\rangle + r)^d\), donde \(d\) se especifica mediante el parámetro degree, \(r\) mediante coef0.

rbf: \(\exp(-\gamma \|x-x'\|^2)\), donde \(\gamma\) se especifica mediante el parámetro gamma, debe ser mayor que 0.

sigmoide: \(\tanh(\gamma \langle x,x'\rangle + r)\), donde \(r\) está especificado por coef0.

Los diferentes núcleos se especifican con el parámetro kernel:

>>> linear_svc = svm.SVC(kernel='linear')
>>> linear_svc.kernel
'linear'
>>> rbf_svc = svm.SVC(kernel='rbf')
>>> rbf_svc.kernel
'rbf'

1.4.6.1. Parámetros del núcleo RBF¶

Cuando se entrena una SVM con el núcleo de Función de Base Radial (Radial Basis Function, RBF), se deben considerar dos parámetros: C y gamma. El parámetro C, común a todos los núcleos SVM, compensa la clasificación incorrecta de los ejemplos de entrenamiento con la simplicidad de la superficie de decisión. Un valor bajo de C hace que la superficie de decisión sea suave, mientras que un valor alto de C tiene como objetivo clasificar correctamente todos los ejemplos de entrenamiento. gamma define cuánta influencia tiene un solo ejemplo de entrenamiento. Cuanto mayor sea gamma, más cerca deben estar otros ejemplos para verse afectados.

La elección adecuada de C y gamma es crítica para el rendimiento de la SVM. Se aconseja utilizar GridSearchCV con C y gamma espaciados exponencialmente para elegir buenos valores.

Ejemplos:

1.4.6.2. Núcleos personalizados¶

Puedes definir tus propios núcleos proporcionando el núcleo como una función python o precalculando la matriz de Gram.

Los clasificadores con núcleos personalizados se comportan de la misma manera que cualquier otro clasificador, excepto que:

El campo support_vectors_ ahora está vacío, sólo los índices de los vectores de soporte se almacenan en support_

Se almacena una referencia (y no una copia) del primer argumento del método fit() para futuras referencias. Si ese arreglo cambia entre el uso de fit() y predict() tendrás resultados inesperados.

1.4.6.2.1. Utilizando funciones de Python como núcleos¶

Puedes utilizar tus propios núcleos definidos pasando una función al parámetro kernel.

Tu kernel debe tomar como argumentos dos matrices de forma (n_samples_1, n_features), (n_samples_2, n_features) y devolver una matriz del kernel de forma (n_samples_1, n_samples_2).

El siguiente código define un núcleo lineal y crea una instancia del clasificador que utilizará ese núcleo:

>>> import numpy as np
>>> from sklearn import svm
>>> def my_kernel(X, Y):
...     return np.dot(X, Y.T)
...
>>> clf = svm.SVC(kernel=my_kernel)

Ejemplos:

SVM con núcleo personalizado.

1.4.6.2.2. Utilizando la matriz de Gram¶

Puedes pasar núcleos precalculados utilizando la opción kernel='precomputed'. Entonces debes pasar la matriz de Gram en lugar de X a los métodos fit y predict. Los valores del núcleo entre todos los vectores de entrenamiento y los vectores de prueba deben ser proporcionados:

>>> import numpy as np
>>> from sklearn.datasets import make_classification
>>> from sklearn.model_selection import train_test_split
>>> from sklearn import svm
>>> X, y = make_classification(n_samples=10, random_state=0)
>>> X_train , X_test , y_train, y_test = train_test_split(X, y, random_state=0)
>>> clf = svm.SVC(kernel='precomputed')
>>> # linear kernel computation
>>> gram_train = np.dot(X_train, X_train.T)
>>> clf.fit(gram_train, y_train)
SVC(kernel='precomputed')
>>> # predict on training examples
>>> gram_test = np.dot(X_test, X_train.T)
>>> clf.predict(gram_test)
array([0, 1, 0])

1.4.7. Formulación matemática¶

Una máquina de vectores de soporte construye un hiperplano o un conjunto de hiperplanos en un espacio de dimensión alta o infinita, que puede utilizarse para la clasificación, la regresión u otras tareas. Intuitivamente, una buena separación se consigue con el hiperplano que tiene la mayor distancia a los puntos de datos de entrenamiento más cercanos de cualquier clase (el llamado margen funcional), ya que en general cuanto mayor sea el margen menor será el error de generalización del clasificador. La figura siguiente muestra la función de decisión para un problema linealmente separable, con tres muestras en las fronteras del margen, llamadas «vectores de soporte»:

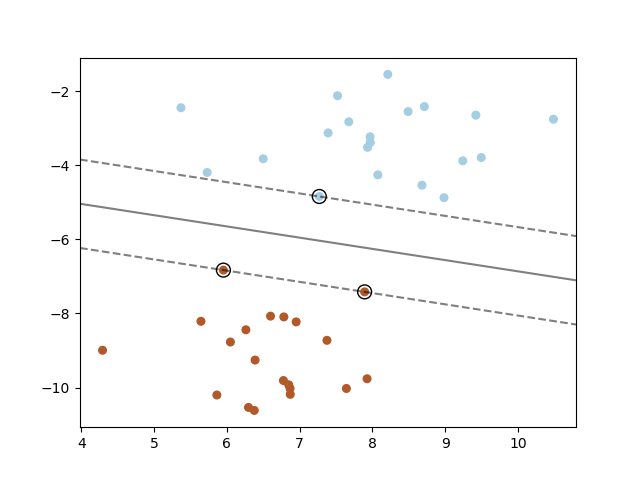
../_images/sphx_glr_plot_separating_hyperplane_001.png

En general, cuando el problema no es linealmente separable, los vectores de soporte son las muestras dentro de las fronteras del margen.

Recomendamos 13 y 14 como buenas referencias para la teoría y los aspectos prácticos de las SVMs.

1.4.7.1. SVC¶

Dados los vectores de entrenamiento \(x_i \in \mathbb{R}^p\), i=1,… , n, en dos clases, y un vector \(y \in \{1, -1\}^n\), nuestro objetivo es encontrar \(w \in \mathbb{R}^p\) y \(b \in \mathbb{R}\) tal que la predicción dada por \(text{sign} (w^T\phi(x) + b)\) sea correcta para la mayoría de las muestras.

SVC resuelve el siguiente problema primal:

\[ \begin{align}\begin{aligned}\min_ {w, b, \zeta} \frac{1}{2} w^T w + C \sum_{i=1}^{n} \zeta_i\\\begin{split}\textrm {subject to } & y_i (w^T \phi (x_i) + b) \geq 1 - \zeta_i,\\ & \zeta_i \geq 0, i=1, ..., n\end{split}\end{aligned}\end{align} \]

Intuitivamente, estamos tratando de maximizar el margen (minimizando \(|w||^2 = w^Tw\)), mientras que se incurre en una penalización cuando una muestra está mal clasificada o dentro de la frontera del margen. Idealmente, el valor \(y_i (w^T \phi (x_i) + b)\) sería \(\geq 1\) para todas las muestras, lo que indica una predicción perfecta. Pero los problemas no suelen ser siempre perfectamente separables con un hiperplano, por lo que permitimos que algunas muestras estén a una distancia \(\zeta_i\) de su frontera de margen correcta. El término de penalización C controla la fuerza de esta penalización, y como resultado, actúa como un parámetro de regularización inversa (ver la nota más abajo).

El problema dual al primal es

\[ \begin{align}\begin{aligned}\min_{\alpha} \frac{1}{2} \alpha^T Q \alpha - e^T \alpha\\\begin{split} \textrm {subject to } & y^T \alpha = 0\\ & 0 \leq \alpha_i \leq C, i=1, ..., n\end{split}\end{aligned}\end{align} \]

donde \(e\) es el vector de unos, y \(Q\) es una matriz semidefinida positiva \(n\) por \(n\), \(Q_{ij} \equiv y_i y_j K(x_i, x_j)\), donde \(K(x_i, x_j) = \phi (x_i)^T \phi (x_j)\) es el núcleo. Los términos \(alpha_i\) se denominan coeficientes duales y están limitados superiormente por \(C\). Esta representación dual resalta el hecho de que los vectores de entrenamiento son implícitamente mapeados en un espacio dimensional superior (tal vez infinito) por la función \(\phi\): ver truco del núcleo.

Una vez resuelto el problema de optimización, la salida de decision_function para una muestra dada \(x\) se convierte en:

\[\sum_{i\in SV} y_i \alpha_i K(x_i, x) + b,\]

y la clase predicha corresponde a su signo. Sólo necesitamos sumar sobre los vectores de soporte (es decir, las muestras que se encuentran dentro del margen) porque los coeficientes duales \(\alpha_i\) son cero para las demás muestras.

Se puede acceder a estos parámetros a través de los atributos dual_coef_ que contiene el producto \(y_i \alpha_i\), support_vectors_ que contiene los vectores de soporte, e intercept_ que contiene el término independiente \(b\)

Nota

Mientras que los modelos SVM derivados de libsvm y liblinear utilizan C como parámetro de regularización, la mayoría de los demás estimadores utilizan alpha. La equivalencia exacta entre la cantidad de regularización de dos modelos depende de la función objetivo exacta optimizada por el modelo. Por ejemplo, cuando el estimador utilizado es la regresión Ridge, la relación entre ellos viene dada como \(C = \frac{1}{alpha}\).

1.4.7.2. LinearSVC¶

El problema primal puede formularse de forma equivalente como

\[\min_ {w, b} \frac{1}{2} w^T w + C \sum_{i=1}\max(0, y_i (w^T \phi(x_i) + b)),\]

donde hacemos uso de la pérdida de bisagra. Esta es la forma que se optimiza directamente con LinearSVC, pero a diferencia de la forma dual, ésta no implica productos internos entre muestras, por lo que no se puede aplicar el famoso truco del núcleo. Por ello, sólo el núcleo lineal es soportado por LinearSVC (\(\phi\) es la función de identidad).

1.4.7.3. NuSVC¶

La formulación \(\nu\)-SVC 15 es una reparametrización de la \(C\)-SVC y, por lo tanto, es matemáticamente equivalente.

Introducimos un nuevo parámetro \(\nu\) (en lugar de \(C\)) que controla el número de vectores de soporte y los errores de margen: \(\nu \in (0, 1]\) es un límite superior de la fracción de errores de margen y un límite inferior de la fracción de vectores de soporte. Un error de margen corresponde a una muestra que se encuentra en el lado incorrecto de su frontera de margen: o bien está mal clasificada, o bien está correctamente clasificada pero no se encuentra más allá del margen.

1.4.7.4. SVR¶

Dados los vectores de entrenamiento \(x_i \in \mathbb{R}^p\), i=1,…, n, y un vector \(y \in \mathbb{R}^n\) \(\varepsilon\)-SVR resuelve el siguiente problema primal:

\[ \begin{align}\begin{aligned}\min_ {w, b, \zeta, \zeta^*} \frac{1}{2} w^T w + C \sum_{i=1}^{n} (\zeta_i + \zeta_i^*)\\\begin{split}\textrm {subject to } & y_i - w^T \phi (x_i) - b \leq \varepsilon + \zeta_i,\\ & w^T \phi (x_i) + b - y_i \leq \varepsilon + \zeta_i^*,\\ & \zeta_i, \zeta_i^* \geq 0, i=1, ..., n\end{split}\end{aligned}\end{align} \]

Aquí, estamos penalizando las muestras cuya predicción está al menos \(\varepsilon\) lejos de su verdadero objetivo. Estas muestras penalizan al objetivo por \(\zeta_i\) o \(\zeta_i^*\), dependiendo de si sus predicciones se encuentran por encima o por debajo del tubo de \(\varepsilon\).

El problema dual es

\[ \begin{align}\begin{aligned}\min_{\alpha, \alpha^*} \frac{1}{2} (\alpha - \alpha^*)^T Q (\alpha - \alpha^*) + \varepsilon e^T (\alpha + \alpha^*) - y^T (\alpha - \alpha^*)\\\begin{split} \textrm {subject to } & e^T (\alpha - \alpha^*) = 0\\ & 0 \leq \alpha_i, \alpha_i^* \leq C, i=1, ..., n\end{split}\end{aligned}\end{align} \]

donde \(e\) es el vector de unos, \(Q\) es una matriz semidefinida positiva \(n\) por \(n\), \(Q_{ij} \equiv K(x_i, x_j) = \phi (x_i)^T \phi (x_j)\) es el núcleo. Aquí los vectores de entrenamiento son implícitamente mapeados en un espacio dimensional superior (quizás infinito) por la función \(\phi\).

La predicción es:

\[\sum_{i \in SV}(\alpha_i - \alpha_i^*) K(x_i, x) + b\]

Se puede acceder a estos parámetros a través de los atributos dual_coef_ que contiene la diferencia \(\alpha_i - \alpha_i^*\), support_vectors_ que contiene los vectores de soporte, e intercept_ que contiene el término independiente \(b\)

1.4.7.5. LinearSVR¶

El problema primal puede formularse de forma equivalente como

\[\min_ {w, b} \frac{1}{2} w^T w + C \sum_{i=1}\max(0, |y_i - (w^T \phi(x_i) + b)| - \varepsilon),\]

donde hacemos uso de la pérdida insensible a épsilon, es decir, los errores menores que \(\varepsilon\) se ignoran. Esta es la forma que se optimiza directamente con LinearSVR.

1.4.8. Detalles de implementación¶

Internamente, usamos libsvm 12 y liblinear 11 para manejar todos los cálculos. Estas bibliotecas están wrapped usando C y Cython. Para una descripción de la implementación y los detalles de los algoritmos utilizados, por favor, consulta sus respectivos documentos.

Referencias:

9: Platt «Probabilistic outputs for SVMs and comparisons to regularized likelihood methods».
10: Wu, Lin y Weng, «Probability estimates for multi-class classification by pairwise coupling», JMLR 5:975-1005, 2004.
11(1,2): Fan, Rong-En, et al., «LIBLINEAR: A library for large linear classification.», Journal of machine learning research 9. Ago. (2008): 1871-1874.
12(1,2): Chang y Lin, LIBSVM: A Library for Support Vector Machines.
13: Bishop, Pattern recognition and machine learning, capítulo 7 Sparse Kernel Machines
14: «A Tutorial on Support Vector Regression», Alex J. Smola, Bernhard Schölkopf - Archivo de Statistics and Computing Volumen 14 Número 3, Agosto 2004, págs. 199-222.
15: Schölkopf et. al New Support Vector Algorithms
16: Crammer y Singer On the Algorithmic Implementation of Multiclass Kernel-based Vector Machines, JMLR 2001.