2.7. Detección de novedades y valores atípicos

Muchas aplicaciones requieren poder decidir si una nueva observación pertenece a la misma distribución que las observaciones existentes (es un valor típico), o debe considerarse como diferente (es un valor atípico). A menudo, esta capacidad se utiliza para limpiar conjuntos de datos reales. Hay que hacer dos distinciones importantes:

detección de valores atípicos

Los datos de entrenamiento contienen valores atípicos que se definen como observaciones que se alejan de las demás. Por tanto, los estimadores de detección de valores atípicos intentan ajustarse a las regiones donde los datos de entrenamiento están más concentrados, ignorando las observaciones desviadas.

detección de novedades

Los datos de entrenamiento no están contaminados por valores atípicos y nos interesa detectar si una nueva observación es un valor atípico. En este contexto, un valor atípico también se denomina novedades.

Tanto la detección de valores atípicos como la detección de novedades se utilizan para la detección de anomalías, cuando uno está interesado en detectar observaciones anormales o inusuales. La detección de valores atípicos también se conoce como detección de anomalías no supervisada y la detección de novedades como detección de anomalías semisupervisada. En el contexto de la detección de valores atípicos, los valores atípicos/anomalías no pueden formar un grupo denso, ya que los estimadores disponibles suponen que los valores atípicos/anomalías se encuentran en regiones de baja densidad. Por el contrario, en el contexto de la detección de novedades, las novedades/anomalías pueden formar un conglomerado denso siempre que se encuentren en una región de baja densidad de los datos de entrenamiento, considerada como normal en este contexto.

El proyecto scikit-learn proporciona un conjunto de herramientas de aprendizaje automático que pueden ser utilizadas tanto para la detección de novedades como para la detección de valores atípicos. Esta estrategia se implementa con el aprendizaje de objetos de una manera no supervisada de los datos:

estimator.fit(X_train)

las observaciones nuevas pueden ser ordenadas como valores típicos y atípicos con un predict método:

estimator.predict(X_test)

Los valores típicos se etiquetan con 1, mientras que los valores atípicos se etiquetan con -1. El método de predicción utiliza un umbral en la función de puntuación bruta calculada por el estimador. Esta función de puntuación es accesible a través del método score_samples, mientras que el umbral puede ser controlado por el parámetro contamination.

El método ``decision_function”” también se define a partir de la función de puntuación, de manera que los valores negativos son valores atípicos y los no negativos son valores atípicos:

estimator.decision_function(X_test)

Ten en cuenta que neighbors.LocalOutlierFactor no admite los métodos predict, decision_function y score_samples por defecto, sino sólo un método fit_predict, ya que este estimador fue concebido originalmente para ser aplicado para la detección de valores atípicos. Las puntuaciones de anormalidad de las muestras de entrenamiento son accesibles a través del atributo negative_outlier_factor_.

Si realmente deseas utilizar neighbors.LocalOutlierFactor para la detección de novedades, es decir, predecir etiquetas o calcular la puntuación de anormalidad de nuevos datos no vistos, puede instanciar el estimador con el parámetro novelty establecido en True antes de ajustar el estimador. En este caso, fit_predict no está disponible.

Advertencia

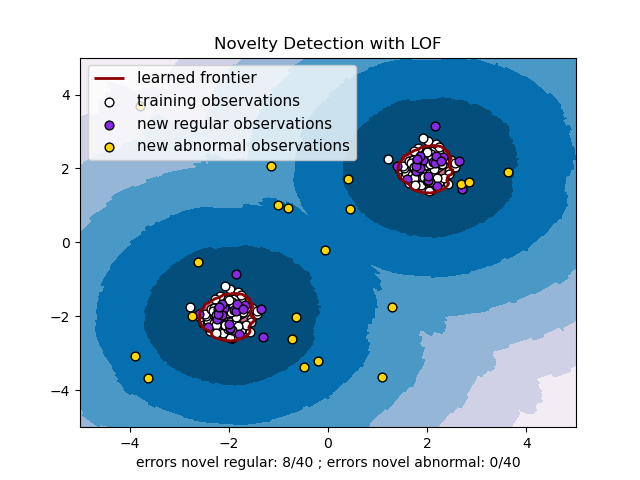
Detección de novedades con Local Outlier Factor

Cuando novelty se establece en True hay que tener en cuenta que sólo debe utilizar predict, decision_function y score_samples en los nuevos datos no vistos y no en las muestras de entrenamiento ya que esto llevaría a resultados erróneos. Las puntuaciones de anormalidad de las muestras de entrenamiento son siempre accesibles a través del atributo negative_outlier_factor_.

El comportamiento de neighbors.LocalOutlierFactor se resume en la siguiente tabla.

Method

Outlier detection

Novelty detection

fit_predict

OK

Not available

predict

Not available

Use only on new data

decision_function

Not available

Use only on new data

score_samples

Use negative_outlier_factor_

Use only on new data

2.7.1. Resumen de los métodos de detección de valores atípicos

Una comparación de los algoritmos de detección de valores atípicos en scikit-learn. Local Outlier Factor (LOF) no muestra un límite de decisión en negro ya que no tiene un método de predicción que se aplique a los nuevos datos cuando se utiliza para la detección de valores atípicos.

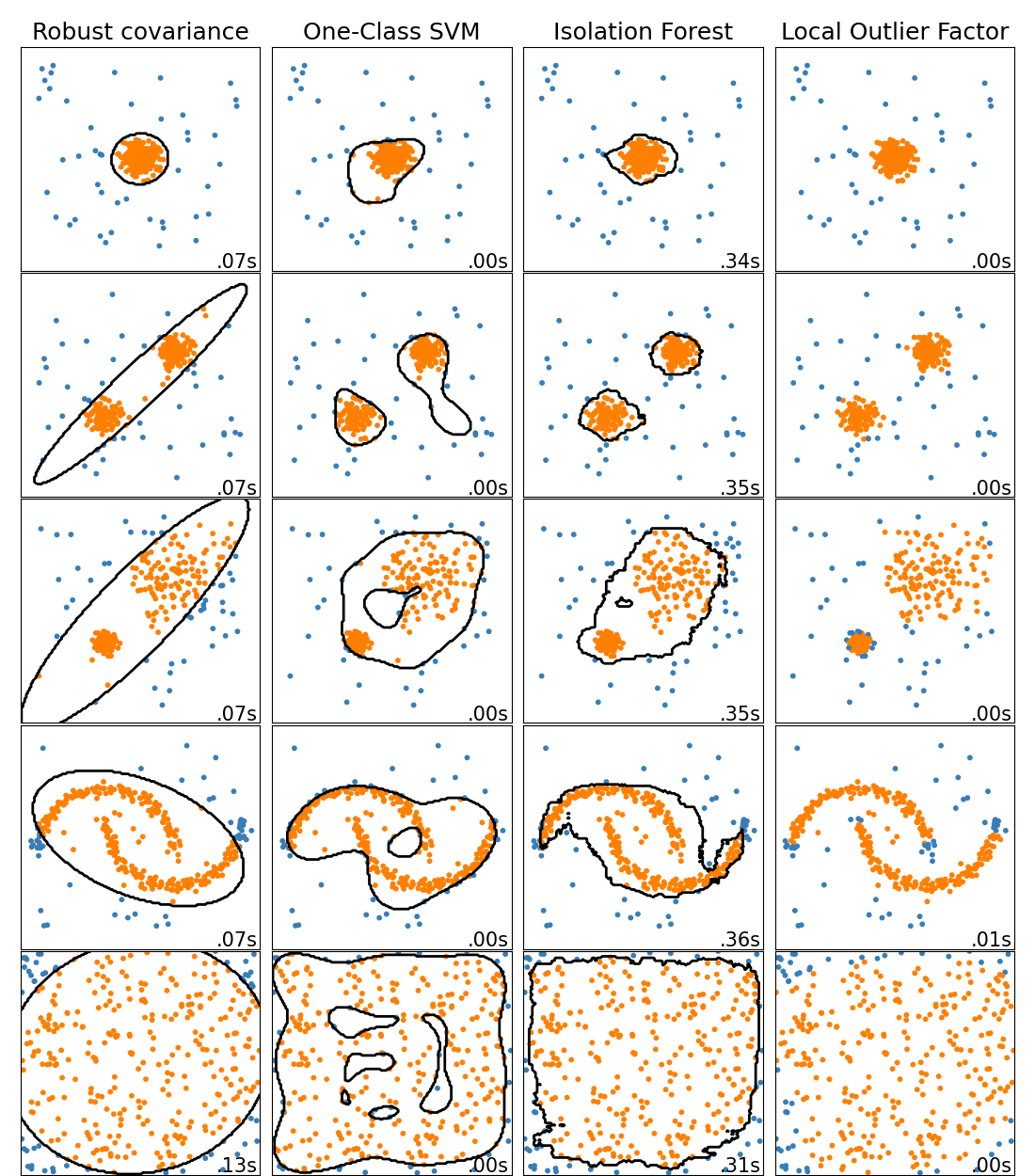
../_images/sphx_glr_plot_anomaly_comparison_001.png

ensemble.IsolationForest y neighbors.LocalOutlierFactor funcionan razonablemente bien en los conjuntos de datos considerados aquí. Se sabe que el svm.OneClassSVM es sensible a los valores atípicos y, por tanto, no funciona muy bien para la detección de valores atípicos. Dicho esto, la detección de valores atípicos en alta dimensión, o sin ningún tipo de suposición sobre la distribución de los datos subyacentes, es un gran reto. svm.OneClassSVM aún puede utilizarse con la detección de valores atípicos, pero requiere un ajuste fino de su hiperparámetro nu para manejar los valores atípicos y evitar el sobreajuste. Por último, covariance.EllipticEnvelope asume que los datos son gaussianos y aprende una elipse. Para más detalles sobre los diferentes estimadores, consulta el ejemplo Comparación de algoritmos de detección de valores atípicos en conjuntos de datos de juguete y las secciones siguientes.

Ejemplos:

2.7.2. Detección de novedades

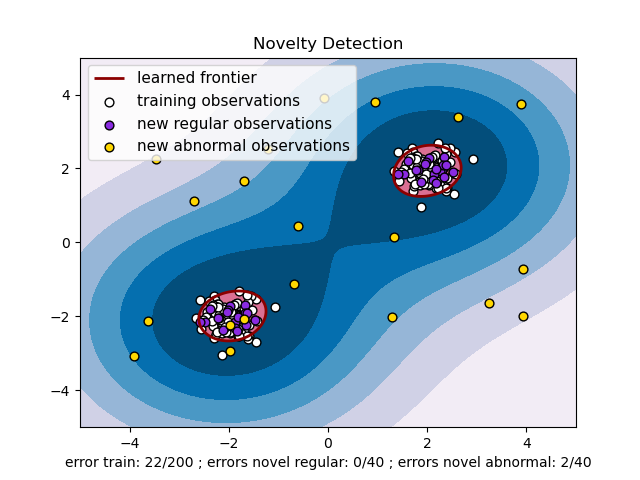
Considere un conjunto de datos de \(n\) observaciones de la misma distribución descrita por las características \(p\). Considere ahora que añadimos una observación más a ese conjunto de datos. ¿Es la nueva observación tan diferente de las demás que podemos dudar de que sea regular? (es decir, ¿procede de la misma distribución?) O, por el contrario, ¿es tan parecida a las demás que no podemos distinguirla de las observaciones originales? Esta es la cuestión que abordan las herramientas y métodos de detección de novedades.

En general, se trata de aprender una frontera aproximada y cercana que delimita el contorno de la distribución de las observaciones iniciales, graficada en el espacio \(p\)-dimensional. Entonces, si las observaciones posteriores se encuentran dentro del subespacio delimitado por la frontera, se considera que proceden de la misma población que las observaciones iniciales. En caso contrario, si se encuentran fuera de la frontera, podemos decir que son anormales con una confianza determinada en nuestra valoración.

La SVM de una clase ha sido introducida por Schölkopf et al. con este fin y se ha implementado en el módulo Máquinas de Vectores de Soporte en el objeto svm.OneClassSVM. Requiere la elección de un kernel y un parámetro escalar para definir una frontera. Normalmente se elige el kernel RBF aunque no existe una fórmula o algoritmo exacto para establecer su parámetro de ancho de banda. Este es el valor por defecto en la implementación de scikit-learn. El parámetro nu, también conocido como el margen de la SVM de una clase, corresponde a la probabilidad de encontrar una nueva, pero regular, observación fuera de la frontera.

Referencias:

Ejemplos:

../_images/sphx_glr_plot_oneclass_001.png

2.7.3. Detección de valores atípicos

La detección de valores atípicos es similar a la detección de novedades en el sentido de que el objetivo es separar un núcleo de observaciones regulares de otras contaminantes, denominadas valores atípicos. Sin embargo, en el caso de la detección de valores atípicos, no disponemos de un conjunto de datos limpio que represente la población de observaciones regulares que pueda utilizarse para entrenar cualquier herramienta.

2.7.3.1. Ajuste de una envolvente elíptica

Una forma habitual de realizar la detección de valores atípicos es suponer que los datos regulares proceden de una distribución conocida (por ejemplo, los datos tienen una distribución gaussiana). A partir de esta suposición, generalmente se intenta definir la «forma» de los datos, y se pueden definir las observaciones atípicas como observaciones que se alejan lo suficiente de la forma ajustada.

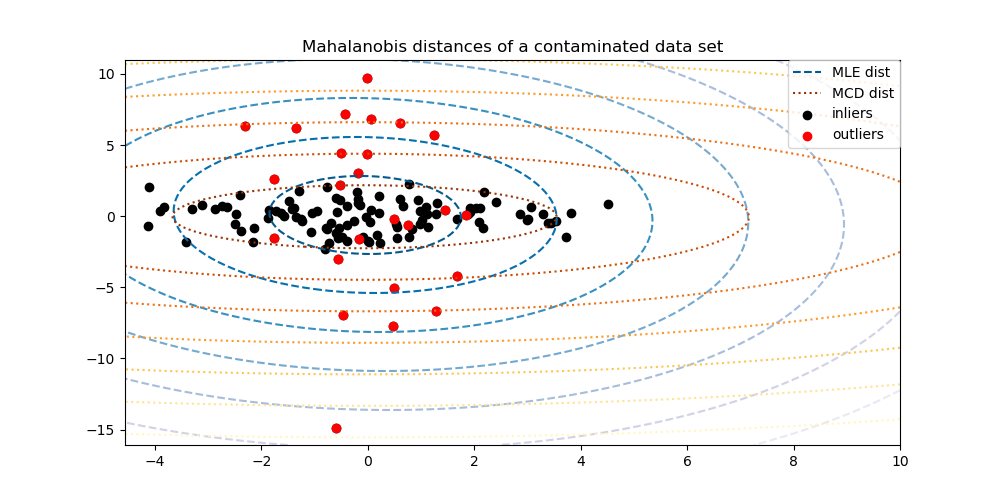
El scikit-learn proporciona un objeto covariance.EllipticEnvelope que ajusta una estimación robusta de la covarianza a los datos, y por tanto ajusta una elipse a los puntos centrales de los datos, ignorando los puntos fuera del modo central.

Por ejemplo, suponiendo que los datos de los inlays se distribuyen de forma gaussiana, estimará la ubicación de los inlays y la covarianza de forma robusta (es decir, sin que se vean influidos por los inlays). Las distancias de Mahalanobis obtenidas a partir de esta estimación se utilizan para obtener una medida de los valores atípicos. Esta estrategia se ilustra a continuación.

../_images/sphx_glr_plot_mahalanobis_distances_001.png

Ejemplos:

Referencias:

  • Rousseeuw, P.J., Van Driessen, K. «A fast algorithm for the minimum covariance determinant estimator» Technometrics 41(3), 212 (1999)

2.7.3.2. Bosque de aislamiento

Una forma eficiente de realizar la detección de valores atípicos en conjuntos de datos de alta dimensión es utilizar bosques aleatorios. La ensemble.IsolationForest “aísla” las observaciones seleccionando aleatoriamente una característica y, a continuación, seleccionando aleatoriamente un valor de división entre los valores máximo y mínimo de la característica seleccionada.

Dado que la partición recursiva puede representarse mediante una estructura de árbol, el número de particiones necesarias para aislar una muestra es equivalente a la longitud del camino desde el nodo raíz hasta el nodo final.

Esta longitud del recorrido, promediada sobre un bosque de tales árboles aleatorios, es una medida de normalidad y nuestra función de decisión.

La partición aleatoria produce trayectorias notablemente más cortas para las anomalías. Por lo tanto, cuando un bosque de árboles aleatorios produce colectivamente trayectorias más cortas para determinadas muestras, es muy probable que se trate de anomalías.

La implementación de ensemble.IsolationForest se basa en un conjunto de tree.ExtraTreeRegressor. Siguiendo el documento original de Isolation Forest, la profundidad máxima de cada árbol se establece en \(\lceil \log_2(n) \rceil\) donde \(n\) es el número de muestras utilizadas para construir el árbol (ver en (Liu et al., 2008) para más detalles).

Este algoritmo se ilustra a continuación.

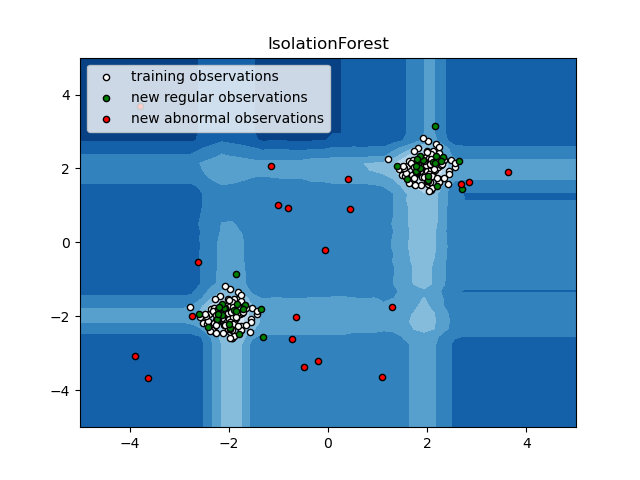
../_images/sphx_glr_plot_isolation_forest_001.png

La ensemble.IsolationForest soporta warm_start=True que permite añadir más árboles a un modelo ya ajustado:

>>> from sklearn.ensemble import IsolationForest
>>> import numpy as np
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [0, 0], [-20, 50], [3, 5]])
>>> clf = IsolationForest(n_estimators=10, warm_start=True)
>>> clf.fit(X)  # fit 10 trees  
>>> clf.set_params(n_estimators=20)  # add 10 more trees  
>>> clf.fit(X)  # fit the added trees

Ejemplos:

Referencias:

  • Liu, Fei Tony, Ting, Kai Ming and Zhou, Zhi-Hua. «Isolation forest.» Data Mining, 2008. ICDM’08. Eighth IEEE International Conference on.

2.7.3.3. Local Outlier Factor

Otra forma eficaz de realizar la detección de valores atípicos en conjuntos de datos moderadamente dimensionales es utilizar el algoritmo del factor local de valores atípicos (LOF).

El algoritmo neighbors.LocalOutlierFactor (LOF) calcula una puntuación (denominada factor local de valores atípicos) que refleja el grado de anormalidad de las observaciones. Mide la desviación de la densidad local de un punto de datos dado con respecto a sus vecinos. La idea es detectar las muestras que tienen una densidad sustancialmente inferior a la de sus vecinos.

En la práctica, la densidad local se obtiene a partir de los k vecinos más cercanos. La puntuación LOF de una observación es igual a la relación entre la densidad local media de sus k vecinos más cercanos y su propia densidad local: se espera que una instancia normal tenga una densidad local similar a la de sus vecinos, mientras que se espera que los datos anormales tengan una densidad local mucho menor.

El número k de vecinos considerado, (parámetro alias n_neighbors) suele elegirse 1) mayor que el número mínimo de objetos que debe contener un clúster, para que otros objetos puedan ser valores atípicos locales en relación con este conglomerado, y 2) menor que el número máximo de objetos cercanos que pueden ser potencialmente atípicos locales. En la práctica, esta información no suele estar disponible, y tomar n_neighbors=20 parece funcionar bien en general. Cuando la proporción de valores atípicos es alta (es decir, superior al 10 %, como en el ejemplo siguiente), n_neighbors debe ser mayor (n_neighbors=35 en el ejemplo siguiente).

El punto fuerte del algoritmo LOF es que tiene en cuenta tanto las propiedades locales como las globales de los conjuntos de datos: puede funcionar bien incluso en conjuntos de datos en los que las muestras anormales tienen diferentes densidades subyacentes. La cuestión no es cuán aislada está la muestra, sino cuán aislada está con respecto al vecindario circundante.

Cuando se aplica LOF para la detección de valores atípicos, no existen los métodos predict, decision_function y score_samples, sino sólo un método fit_predict. Las puntuaciones de anormalidad de las muestras de entrenamiento son accesibles a través del atributo negative_outlier_factor_. Tenga en cuenta que predict, decision_function y score_samples pueden utilizarse en nuevos datos no vistos cuando se aplica LOF para la detección de novedades, es decir, cuando el parámetro novelty se establece en True. Ver en Detección de novedades con Local Outlier Factor.

Esta estrategia se ilustra a continuación.

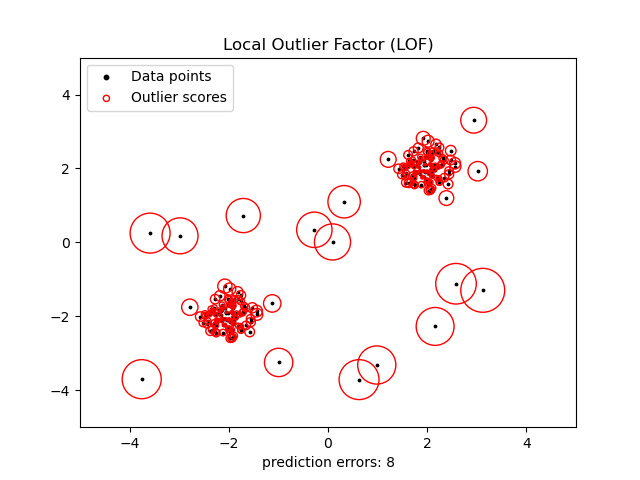
../_images/sphx_glr_plot_lof_outlier_detection_001.png

Ejemplos:

Referencias:

2.7.4. Detección de novedades con Local Outlier Factor

Para utilizar neighbors.LocalOutlierFactor para la detección de novedades, es decir, para predecir etiquetas o calcular la puntuación de anormalidad de nuevos datos no vistos, es necesario instanciar el estimador con el parámetro novelty establecido en True antes de ajustar el estimador:

lof = LocalOutlierFactor(novelty=True)
lof.fit(X_train)

Toma en cuenta que fit_predict no está disponible en este caso.

Advertencia

Detección de novedades con Local Outlier Factor`

Cuando novelty se establece en True hay que tener en cuenta que sólo debe utilizar predict, decision_function y score_samples en los nuevos datos no vistos y no en las muestras de entrenamiento ya que esto llevaría a resultados erróneos. Las puntuaciones de anormalidad de las muestras de entrenamiento son siempre accesibles a través del atributo negative_outlier_factor_.

A continuación, se ilustra la detección de novedades con Local Outlier Factor.

../_images/sphx_glr_plot_lof_novelty_detection_001.png