Estimación robusta de la covarianza y relevancia de las distancias de Mahalanobis

Este ejemplo muestra la estimación de la covarianza con distancias de Mahalanobis en datos con distribución gaussiana.

Para los datos con distribución gaussiana, la distancia de una observación \(x_i\) a la moda de la distribución puede calcularse utilizando su distancia de Mahalanobis:

\[d_{(\mu,\Sigma)}(x_i)^2 = (x_i - \mu)^T\Sigma^{-1}(x_i - \mu)\]

donde \(\mu\) y \(\Sigma\) son la localización y la covarianza de las distribuciones gaussianas subyacentes.

En la práctica, \(\mu\) y \(\Sigma\) se sustituyen por algunas estimaciones. La estimación estándar de covarianza por máxima verosimilitud (MLE) es muy sensible a la presencia de valores atípicos en el conjunto de datos y, por tanto, las distancias de Mahalanobis descendentes también lo son. Sería mejor utilizar un estimador robusto de la covarianza para garantizar que la estimación es resistente a las observaciones «erróneas» en el conjunto de datos y que las distancias de Mahalanobis calculadas reflejan con precisión la verdadera organización de las observaciones.

El estimador del Determinante Mínimo de la Covarianza (MCD) es un estimador de la covarianza robusto y con un punto de ruptura alto (es decir, puede utilizarse para estimar la matriz de covarianza de conjuntos de datos altamente contaminados, hasta \(\frac{n_\text{samples}-n_\text{features}-1}{2}\) los valores atípicos). La idea detrás del MCD es encontrar observaciones \(\frac{n_\text{samples}+n_\text{features}+1}{2}\) cuya covarianza empírica tenga el menor determinante, produciendo un subconjunto «puro» de observaciones a partir del cual calcular las estimaciones estándar de ubicación y covarianza. El MCD fue introducido por P.J.Rousseuw en 1.

Este ejemplo ilustra cómo las distancias de Mahalanobis se ven afectadas por los datos periféricos. Las observaciones extraídas de una distribución contaminante no se distinguen de las observaciones procedentes de la distribución gaussiana real cuando se utilizan las distancias de Mahalanobis basadas en la covarianza estándar MLE. Con las distancias de Mahalanobis basadas en la MCD, las dos poblaciones se distinguen. Las aplicaciones asociadas incluyen la detección de valores atípicos, la clasificación de observaciones y el conglomerado.

Nota

Ver también Estimación de la covarianza robusta frente a la empírica

Referencias:

1

P. J. Rousseeuw. Least median of squares regression. J. Am Stat Ass, 79:871, 1984.

2

Wilson, E. B., & Hilferty, M. M. (1931). The distribution of chi-square. Proceedings of the National Academy of Sciences of the United States of America, 17, 684-688.

Generar datos

En primer lugar, generamos un conjunto de datos de 125 muestras y 2 características. Ambas características tienen una distribución gaussiana con una media de 0, pero la característica 1 tiene una desviación estándar igual a 2 y la característica 2 tiene una desviación estándar igual a 1. A continuación, se sustituyen 25 muestras por muestras gaussianas de valor atípico en las que la característica 1 tiene una desviación estándar igual a 1 y la característica 2 tiene una desviación estándar igual a 7.

import numpy as np

# for consistent results
np.random.seed(7)

n_samples = 125
n_outliers = 25
n_features = 2

# generate Gaussian data of shape (125, 2)
gen_cov = np.eye(n_features)
gen_cov[0, 0] = 2.
X = np.dot(np.random.randn(n_samples, n_features), gen_cov)
# add some outliers
outliers_cov = np.eye(n_features)
outliers_cov[np.arange(1, n_features), np.arange(1, n_features)] = 7.
X[-n_outliers:] = np.dot(np.random.randn(n_outliers, n_features), outliers_cov)

Comparación de resultados

A continuación, ajustamos los estimadores de covarianza basados en MCD y MLE a nuestros datos e imprimimos las matrices de covarianza estimadas. Obsérvese que la varianza estimada de la característica 2 es mucho mayor con el estimador basado en MLE (7,5) que con el estimador robusto MCD (1,2). Esto muestra que el estimador robusto basado en MCD es mucho más resistente a las muestras de valor atípico, que fueron diseñadas para tener una varianza mucho mayor en la característica 2.

import matplotlib.pyplot as plt
from sklearn.covariance import EmpiricalCovariance, MinCovDet

# fit a MCD robust estimator to data
robust_cov = MinCovDet().fit(X)
# fit a MLE estimator to data
emp_cov = EmpiricalCovariance().fit(X)
print('Estimated covariance matrix:\n'
      'MCD (Robust):\n{}\n'
      'MLE:\n{}'.format(robust_cov.covariance_, emp_cov.covariance_))

Out:

Estimated covariance matrix:
MCD (Robust):
[[ 3.26253567e+00 -3.06695631e-03]
 [-3.06695631e-03  1.22747343e+00]]
MLE:
[[ 3.23773583 -0.24640578]
 [-0.24640578  7.51963999]]

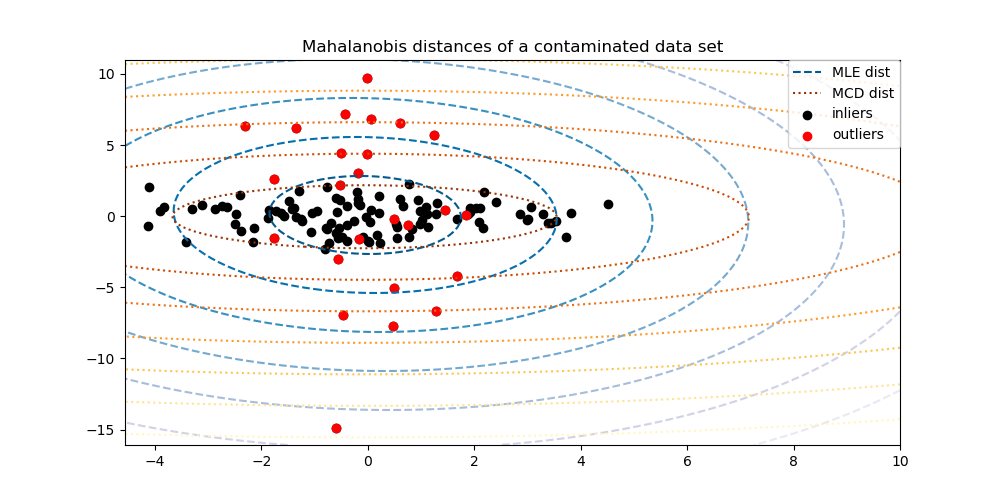
Para visualizar mejor la diferencia, graficamos los contornos de las distancias de Mahalanobis calculadas por ambos métodos. Obsérvese que las distancias de Mahalanobis basadas en el MCD robusto se ajustan mucho mejor a los puntos negros de los valores típicos, mientras que las distancias basadas en el MLE están más influenciadas por los puntos rojos de los valores atípicos.

fig, ax = plt.subplots(figsize=(10, 5))
# Plot data set
inlier_plot = ax.scatter(X[:, 0], X[:, 1],
                         color='black', label='inliers')
outlier_plot = ax.scatter(X[:, 0][-n_outliers:], X[:, 1][-n_outliers:],
                          color='red', label='outliers')
ax.set_xlim(ax.get_xlim()[0], 10.)
ax.set_title("Mahalanobis distances of a contaminated data set")

# Create meshgrid of feature 1 and feature 2 values
xx, yy = np.meshgrid(np.linspace(plt.xlim()[0], plt.xlim()[1], 100),
                     np.linspace(plt.ylim()[0], plt.ylim()[1], 100))
zz = np.c_[xx.ravel(), yy.ravel()]
# Calculate the MLE based Mahalanobis distances of the meshgrid
mahal_emp_cov = emp_cov.mahalanobis(zz)
mahal_emp_cov = mahal_emp_cov.reshape(xx.shape)
emp_cov_contour = plt.contour(xx, yy, np.sqrt(mahal_emp_cov),
                              cmap=plt.cm.PuBu_r, linestyles='dashed')
# Calculate the MCD based Mahalanobis distances
mahal_robust_cov = robust_cov.mahalanobis(zz)
mahal_robust_cov = mahal_robust_cov.reshape(xx.shape)
robust_contour = ax.contour(xx, yy, np.sqrt(mahal_robust_cov),
                            cmap=plt.cm.YlOrBr_r, linestyles='dotted')

# Add legend
ax.legend([emp_cov_contour.collections[1], robust_contour.collections[1],
          inlier_plot, outlier_plot],
          ['MLE dist', 'MCD dist', 'inliers', 'outliers'],
          loc="upper right", borderaxespad=0)

plt.show()

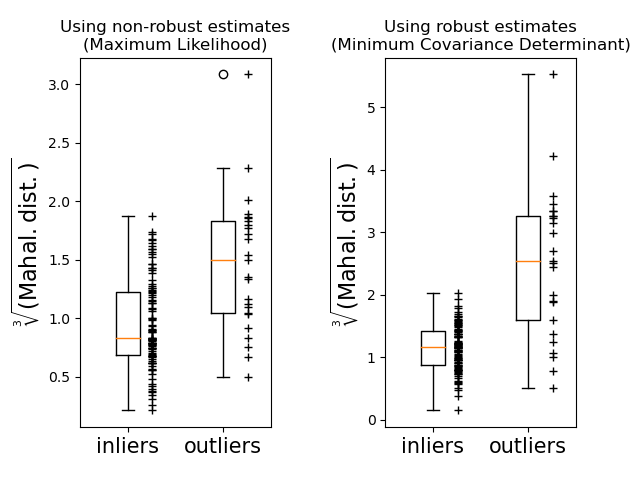
Por último, destacamos la capacidad de las distancias de Mahalanobis basadas en MCD para distinguir los valores atípicos. Tomamos la raíz cúbica de las distancias de Mahalanobis, lo que da lugar a distribuciones aproximadamente normales (como sugieren Wilson y Hilferty 2), y luego trazamos los valores de las muestras de los valores típicos y los valor atípico con boxplots. La distribución de las muestras atípicas está más separada de la distribución de las muestras típicas para el MCD robusto basado en las distancias de Mahalanobis.

fig, (ax1, ax2) = plt.subplots(1, 2)
plt.subplots_adjust(wspace=.6)

# Calculate cubic root of MLE Mahalanobis distances for samples
emp_mahal = emp_cov.mahalanobis(X - np.mean(X, 0)) ** (0.33)
# Plot boxplots
ax1.boxplot([emp_mahal[:-n_outliers], emp_mahal[-n_outliers:]], widths=.25)
# Plot individual samples
ax1.plot(np.full(n_samples - n_outliers, 1.26), emp_mahal[:-n_outliers],
         '+k', markeredgewidth=1)
ax1.plot(np.full(n_outliers, 2.26), emp_mahal[-n_outliers:],
         '+k', markeredgewidth=1)
ax1.axes.set_xticklabels(('inliers', 'outliers'), size=15)
ax1.set_ylabel(r"$\sqrt[3]{\rm{(Mahal. dist.)}}$", size=16)
ax1.set_title("Using non-robust estimates\n(Maximum Likelihood)")

# Calculate cubic root of MCD Mahalanobis distances for samples
robust_mahal = robust_cov.mahalanobis(X - robust_cov.location_) ** (0.33)
# Plot boxplots
ax2.boxplot([robust_mahal[:-n_outliers], robust_mahal[-n_outliers:]],
            widths=.25)
# Plot individual samples
ax2.plot(np.full(n_samples - n_outliers, 1.26), robust_mahal[:-n_outliers],
         '+k', markeredgewidth=1)
ax2.plot(np.full(n_outliers, 2.26), robust_mahal[-n_outliers:],
         '+k', markeredgewidth=1)
ax2.axes.set_xticklabels(('inliers', 'outliers'), size=15)
ax2.set_ylabel(r"$\sqrt[3]{\rm{(Mahal. dist.)}}$", size=16)
ax2.set_title("Using robust estimates\n(Minimum Covariance Determinant)")

plt.show()