Estimación de la covarianza de la contracción: LedoitWolf vs OAS y max-likelihood

Cuando se trabaja con la estimación de la covarianza, el enfoque habitual es utilizar un estimador de máxima verosimilitud, como el EmpiricalCovariance. Es insesgado, es decir, converge a la verdadera covarianza (de la población) cuando se dan muchas observaciones. Sin embargo, también puede ser beneficioso regularizarla, para reducir su varianza; esto, a su vez, introduce algún sesgo. Este ejemplo ilustra la regularización simple utilizada en los estimadores de Covarianza Reducida. En particular, se centra en cómo establecer la cantidad de regularización, es decir, cómo elegir el equilibrio entre sesgo y varianza.

Aquí comparamos 3 enfoques:

• Ajuste del parámetro mediante la validación cruzada de la verosimilitud en tres pliegues según una cuadrícula de posibles parámetros de contracción.

• Una fórmula cercana propuesta por Ledoit y Wolf para calcular el parámetro de regularización asintóticamente óptimo (minimizando un criterio MSE), produciendo la estimación de covarianza LedoitWolf.

• Una mejora de la contracción de Ledoit-Wolf, el OAS, propuesto por Chen et al. Su convergencia es significativamente mejor bajo el supuesto de que los datos son gaussianos, en particular para muestras pequeñas.

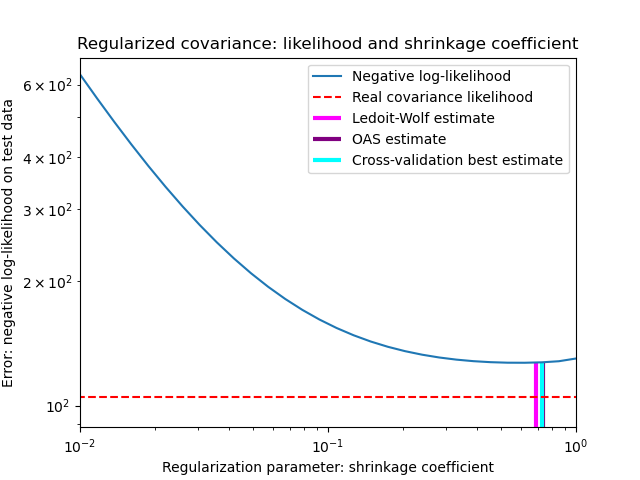
Para cuantificar el error de estimación, graficamos la verosimilitud de los datos no vistos para diferentes valores del parámetro de contracción. También mostramos las opciones por validación cruzada, o con las estimaciones de LedoitWolf y OAS.

Obsérvese que la estimación de máxima verosimilitud corresponde a la ausencia de contracción, por lo que su rendimiento es escaso. La estimación de Ledoit-Wolf funciona muy bien, ya que se acerca al óptimo y no es costosa computacionalmente. En este ejemplo, la estimación de OAS está un poco más lejos. Curiosamente, ambos enfoques superan a la validación cruzada, que es significativamente más costosa computacionalmente.

print(__doc__)

import numpy as np
import matplotlib.pyplot as plt
from scipy import linalg

from sklearn.covariance import LedoitWolf, OAS, ShrunkCovariance, \
    log_likelihood, empirical_covariance
from sklearn.model_selection import GridSearchCV


# #############################################################################
# Generate sample data
n_features, n_samples = 40, 20
np.random.seed(42)
base_X_train = np.random.normal(size=(n_samples, n_features))
base_X_test = np.random.normal(size=(n_samples, n_features))

# Color samples
coloring_matrix = np.random.normal(size=(n_features, n_features))
X_train = np.dot(base_X_train, coloring_matrix)
X_test = np.dot(base_X_test, coloring_matrix)

# #############################################################################
# Compute the likelihood on test data

# spanning a range of possible shrinkage coefficient values
shrinkages = np.logspace(-2, 0, 30)
negative_logliks = [-ShrunkCovariance(shrinkage=s).fit(X_train).score(X_test)
                    for s in shrinkages]

# under the ground-truth model, which we would not have access to in real
# settings
real_cov = np.dot(coloring_matrix.T, coloring_matrix)
emp_cov = empirical_covariance(X_train)
loglik_real = -log_likelihood(emp_cov, linalg.inv(real_cov))

# #############################################################################
# Compare different approaches to setting the parameter

# GridSearch for an optimal shrinkage coefficient
tuned_parameters = [{'shrinkage': shrinkages}]
cv = GridSearchCV(ShrunkCovariance(), tuned_parameters)
cv.fit(X_train)

# Ledoit-Wolf optimal shrinkage coefficient estimate
lw = LedoitWolf()
loglik_lw = lw.fit(X_train).score(X_test)

# OAS coefficient estimate
oa = OAS()
loglik_oa = oa.fit(X_train).score(X_test)

# #############################################################################
# Plot results
fig = plt.figure()
plt.title("Regularized covariance: likelihood and shrinkage coefficient")
plt.xlabel('Regularization parameter: shrinkage coefficient')
plt.ylabel('Error: negative log-likelihood on test data')
# range shrinkage curve
plt.loglog(shrinkages, negative_logliks, label="Negative log-likelihood")

plt.plot(plt.xlim(), 2 * [loglik_real], '--r',
         label="Real covariance likelihood")

# adjust view
lik_max = np.amax(negative_logliks)
lik_min = np.amin(negative_logliks)
ymin = lik_min - 6. * np.log((plt.ylim()[1] - plt.ylim()[0]))
ymax = lik_max + 10. * np.log(lik_max - lik_min)
xmin = shrinkages[0]
xmax = shrinkages[-1]
# LW likelihood
plt.vlines(lw.shrinkage_, ymin, -loglik_lw, color='magenta',
           linewidth=3, label='Ledoit-Wolf estimate')
# OAS likelihood
plt.vlines(oa.shrinkage_, ymin, -loglik_oa, color='purple',
           linewidth=3, label='OAS estimate')
# best CV estimator likelihood
plt.vlines(cv.best_estimator_.shrinkage, ymin,
           -cv.best_estimator_.score(X_test), color='cyan',
           linewidth=3, label='Cross-validation best estimate')

plt.ylim(ymin, ymax)
plt.xlim(xmin, xmax)
plt.legend()

plt.show()