Estimación de la covarianza inversa dispersa

Uso del estimador GraphicalLasso para aprender una covarianza y una precisión dispersa a partir de un pequeño número de muestras.

Para estimar un modelo probabilístico (por ejemplo, un modelo gaussiano), la estimación de la matriz de precisión, es decir, la matriz de covarianza inversa, es tan importante como la estimación de la matriz de covarianza. De hecho, un modelo gaussiano está parametrizado por la matriz de precisión.

Para estar en condiciones favorables de recuperación, muestreamos los datos de un modelo con una matriz de covarianza inversa dispersa. Además, nos aseguramos de que los datos no estén demasiado correlacionados (limitando el mayor coeficiente de la matriz de precisión) y de que no haya coeficientes pequeños en la matriz de precisión que no puedan recuperarse. Además, con un número reducido de observaciones, es más fácil recuperar una matriz de correlación que de covarianza, por lo que escalamos las series de tiempo.

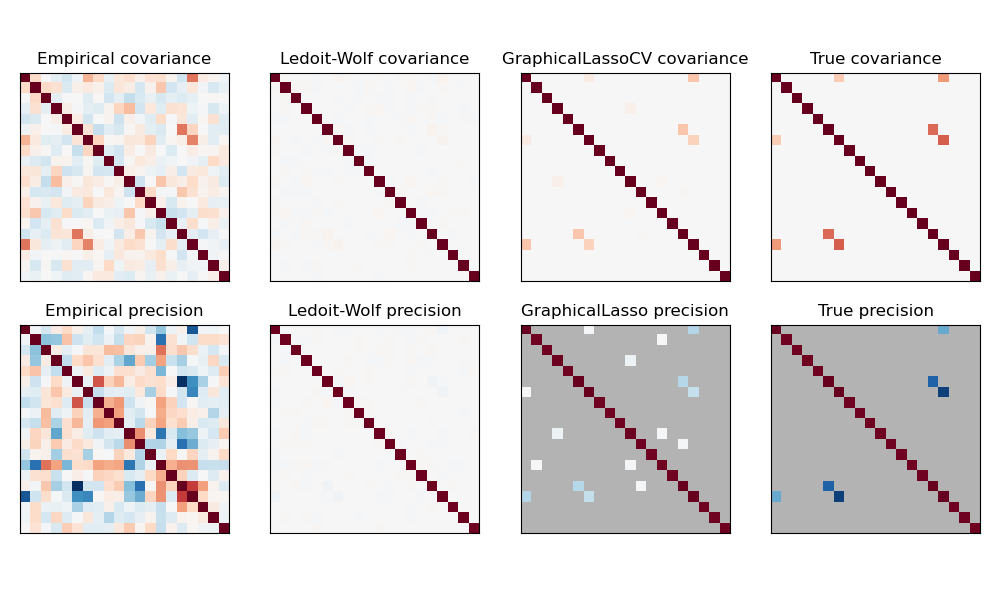
En este caso, el número de muestras es ligeramente mayor que el número de dimensiones, por lo que la covarianza empírica sigue siendo invertible. Sin embargo, como las observaciones están fuertemente correlacionadas, la matriz de covarianza empírica está mal condicionada y, en consecuencia, su inversa –la matriz de precisión empírica– está muy alejada de la verdad fundamental.

Si utilizamos la contracción l2, como con el estimador de Ledoit-Wolf, como el número de muestras es pequeño, tenemos que encoger mucho. Como resultado, la precisión de Ledoit-Wolf se aproxima bastante a la precisión de la verdad fundamental, que no está lejos de ser diagonal, pero se pierde la estructura no diagonal.

El estimador l1-penalizado puede recuperar parte de esta estructura no diagonal. Aprende una precisión dispersa. No es capaz de recuperar el patrón de sparsity exacto: detecta demasiados coeficientes no nulos. Sin embargo, los coeficientes no nulos más altos de l1 estimados corresponden a los coeficientes distinto de cero de la verdad fundamental. Por último, los coeficientes de la estimación de precisión de l1 están sesgados hacia el cero: debido a la penalización, todos son más pequeños que el valor correspondiente de la verdad fundamental, como se puede ver en la figura.

Tenga en cuenta que, el rango de colores de las matrices de precisión se ha ajustado para mejorar la legibilidad de la figura. No se muestra todo el rango de valores de la precisión empírica.

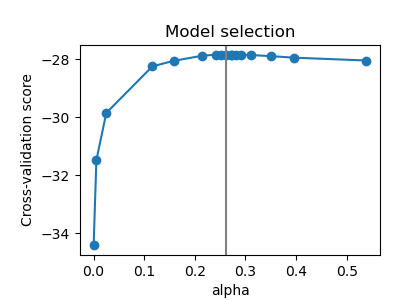
El parámetro alfa del GraphicalLasso que establece la dispersión del modelo se fija mediante la validación cruzada interna en el GraphicalLassoCV. Como se puede ver en la figura 2, la cuadrícula para calcular la puntuación de validación cruzada se refina iterativamente en el vecindario del máximo.

• 
• 

print(__doc__)
# author: Gael Varoquaux <gael.varoquaux@inria.fr>
# License: BSD 3 clause
# Copyright: INRIA

import numpy as np
from scipy import linalg
from sklearn.datasets import make_sparse_spd_matrix
from sklearn.covariance import GraphicalLassoCV, ledoit_wolf
import matplotlib.pyplot as plt

# #############################################################################
# Generate the data
n_samples = 60
n_features = 20

prng = np.random.RandomState(1)
prec = make_sparse_spd_matrix(n_features, alpha=.98,
                              smallest_coef=.4,
                              largest_coef=.7,
                              random_state=prng)
cov = linalg.inv(prec)
d = np.sqrt(np.diag(cov))
cov /= d
cov /= d[:, np.newaxis]
prec *= d
prec *= d[:, np.newaxis]
X = prng.multivariate_normal(np.zeros(n_features), cov, size=n_samples)
X -= X.mean(axis=0)
X /= X.std(axis=0)

# #############################################################################
# Estimate the covariance
emp_cov = np.dot(X.T, X) / n_samples

model = GraphicalLassoCV()
model.fit(X)
cov_ = model.covariance_
prec_ = model.precision_

lw_cov_, _ = ledoit_wolf(X)
lw_prec_ = linalg.inv(lw_cov_)

# #############################################################################
# Plot the results
plt.figure(figsize=(10, 6))
plt.subplots_adjust(left=0.02, right=0.98)

# plot the covariances
covs = [('Empirical', emp_cov), ('Ledoit-Wolf', lw_cov_),
        ('GraphicalLassoCV', cov_), ('True', cov)]
vmax = cov_.max()
for i, (name, this_cov) in enumerate(covs):
    plt.subplot(2, 4, i + 1)
    plt.imshow(this_cov, interpolation='nearest', vmin=-vmax, vmax=vmax,
               cmap=plt.cm.RdBu_r)
    plt.xticks(())
    plt.yticks(())
    plt.title('%s covariance' % name)


# plot the precisions
precs = [('Empirical', linalg.inv(emp_cov)), ('Ledoit-Wolf', lw_prec_),
         ('GraphicalLasso', prec_), ('True', prec)]
vmax = .9 * prec_.max()
for i, (name, this_prec) in enumerate(precs):
    ax = plt.subplot(2, 4, i + 5)
    plt.imshow(np.ma.masked_equal(this_prec, 0),
               interpolation='nearest', vmin=-vmax, vmax=vmax,
               cmap=plt.cm.RdBu_r)
    plt.xticks(())
    plt.yticks(())
    plt.title('%s precision' % name)
    if hasattr(ax, 'set_facecolor'):
        ax.set_facecolor('.7')
    else:
        ax.set_axis_bgcolor('.7')

# plot the model selection metric
plt.figure(figsize=(4, 3))
plt.axes([.2, .15, .75, .7])
plt.plot(model.cv_results_["alphas"], model.cv_results_["mean_score"], 'o-')
plt.axvline(model.alpha_, color='.5')
plt.title('Model selection')
plt.ylabel('Cross-validation score')
plt.xlabel('alpha')

plt.show()