2.6. Estimación de covarianza

Muchos problemas estadísticos requieren la estimación de la matriz de covarianza de una población, que puede considerarse como una estimación de la forma del diagrama de dispersión del conjunto de datos. La mayoría de las veces, esta estimación debe realizarse sobre una muestra cuyas propiedades (tamaño, estructura, homogeneidad) tienen una gran influencia en la calidad de la estimación. El paquete sklearn.covariance proporciona herramientas para la estimación precisa de la matriz de covarianza de una población de acuerdo con varias condiciones.

Asumimos que las observaciones son independientes e idénticamente distribuidas (i.i.d.).

2.6.1. Covarianza empírica

Se sabe que la matriz de covarianza de un conjunto de datos está bien aproximada por el clásico estimador de máxima verosimilitud (o «covarianza empírica»), siempre que el número de observaciones sea lo suficientemente grande en comparación con el número de características (las variables que describen las observaciones). Más concretamente, el estimador de máxima verosimilitud de una muestra es un estimador asintóticamente no sesgado de la matriz de covarianza de la población correspondiente.

La matriz de covarianza empírica de una muestra puede calcularse utilizando la función empirical_covariance del paquete, o ajustando un objeto EmpiricalCovariance a la muestra de datos con el método EmpiricalCovariance.fit. Hay que tener en cuenta que los resultados dependen de si los datos están centrados, por lo que es conveniente utilizar el parámetro assume_centered con precisión. Más concretamente, si assume_centered=False, se supone que el conjunto de prueba tiene el mismo vector medio que el conjunto de entrenamiento. Si no es así, ambos deben ser centrados por el usuario, y se debe utilizar assume_centered=True.

Ejemplos:

2.6.2. Covarianza Reducida

2.6.2.1. Reducción básica

A pesar de ser un estimador asintóticamente no sesgado de la matriz de covarianza, el Estimador de Máxima Verosimilitud no es un buen estimador de los valores propios de la matriz de covarianza, por lo que la matriz de precisión obtenida de su inversión no es exacta. A veces, incluso ocurre que la matriz de covarianza empírica no puede invertirse por razones numéricas. Para evitar este problema de inversión, se ha introducido una transformación de la matriz de covarianza empírica: la reducción (shrinkage).

En scikit-learn, esta transformación (con un coeficiente de contracción definido por el usuario) se puede aplicar directamente a una covarianza precalculada con el método shrunk_covariance. Además, un estimador reducido de la covarianza puede ajustarse a los datos con un objeto ShrunkCovariance y su método ShrunkCovariance.fit. Una vez más, los resultados dependen de si los datos están centrados, por lo que uno puede querer utilizar el parámetro assume_centered con precisión.

Matemáticamente, esta reducción consiste en disminuir la relación entre los valores propios más pequeños y los más grandes de la matriz de covarianza empírica. Puede hacerse simplemente desplazando cada autovalor según un desplazamiento dado, lo que equivale a encontrar el Estimador de Máxima Verosimilitud l2-penalizado de la matriz de covarianza. En la práctica, la reducción se reduce a una simple transformación convexa: \(\Sigma_{\rm shrunk} = (1-\alpha)\hat{\Sigma} + \alpha\frac{\rm Tr}{hat{\Sigma}{p}\rm Id\).

La elección de la cantidad de reducción, \(\alpha\) equivale a establecer un compromiso de sesgo/varianza, que se discute a continuación.

Ejemplos:

2.6.2.2. Reducción de Ledoit-Wolf

En su artículo de 2004 1, O. Ledoit y M. Wolf proponen una fórmula para calcular el coeficiente de reducción óptimo \(\alpha\) que minimiza el error cuadrático medio entre la matriz estimada y la matriz de covarianza real.

El estimador Ledoit-Wolf de la matriz de covarianza puede calcularse sobre una muestra con la función ledoit_wolf del paquete sklearn.covariance, o puede obtenerse de otro modo ajustando un objeto LedoitWolf a la misma muestra.

Nota

Caso cuando la matriz de covarianza de población es isotrópica

Es importante señalar que cuando el número de muestras es mucho mayor que el número de características, cabría esperar que no fuera necesaria ninguna reducción. La intuición detrás de esto es que si la covarianza de la población es de rango completo, cuando el número de muestras crece, la covarianza de la muestra también se convertirá en positiva definida. Por lo tanto, no sería necesaria ninguna reducción y el método debería hacerlo automáticamente.

Sin embargo, esto no ocurre en el procedimiento de Ledoit-Wolf cuando la covarianza de la población resulta ser un múltiplo de la matriz de identidad. En este caso, la estimación de la reducción de Ledoit-Wolf se aproxima a 1 a medida que aumenta el número de muestras. Esto indica que la estimación óptima de la matriz de covarianza en el sentido de Ledoit-Wolf es múltiplo de la identidad. Dado que la covarianza de la población ya es un múltiplo de la matriz de identidad, la solución de Ledoit-Wolf es efectivamente una estimación razonable.

Ejemplos:

Referencias:

1

O. Ledoit and M. Wolf, «A Well-Conditioned Estimator for Large-Dimensional Covariance Matrices», Journal of Multivariate Analysis, Volume 88, Issue 2, February 2004, pages 365-411.

2.6.2.3. Reducción Aproximante de Oracle

Bajo el supuesto de que los datos tienen una distribución gaussiana, Chen et al. 2 derivaron una fórmula destinada a elegir un coeficiente de reducción que produzca un error cuadrático medio menor que el dado por la fórmula de Ledoit y Wolf. El estimador resultante se conoce como estimador de la reducción aproximante de Oracle (OAS) de la covarianza.

El estimador OAS de la matriz de covarianza puede calcularse sobre una muestra con la función oas del paquete sklearn.covariance, o puede obtenerse de otro modo ajustando un objeto OAS a la misma muestra.

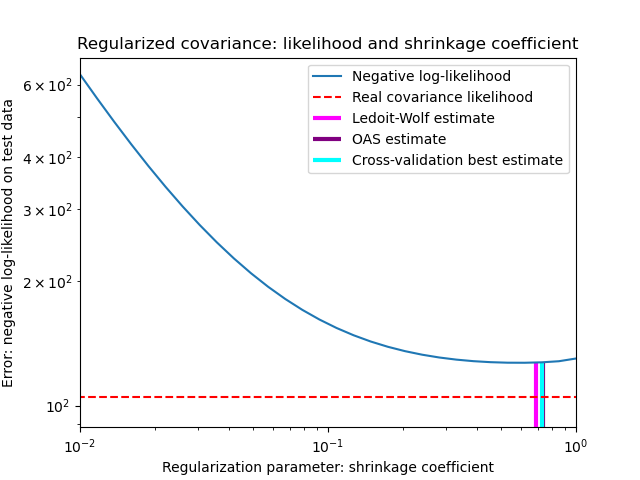
../_images/sphx_glr_plot_covariance_estimation_001.png

Compensación entre el sesgo y la varianza al fijar la reducción: comparación de las opciones de los estimadores Ledoit-Wolf y OAS

Referencias:

2

Chen et al., «Shrinkage Algorithms for MMSE Covariance Estimation», IEEE Trans. on Sign. Proc., Volume 58, Issue 10, Octubre 2010.

Ejemplos:

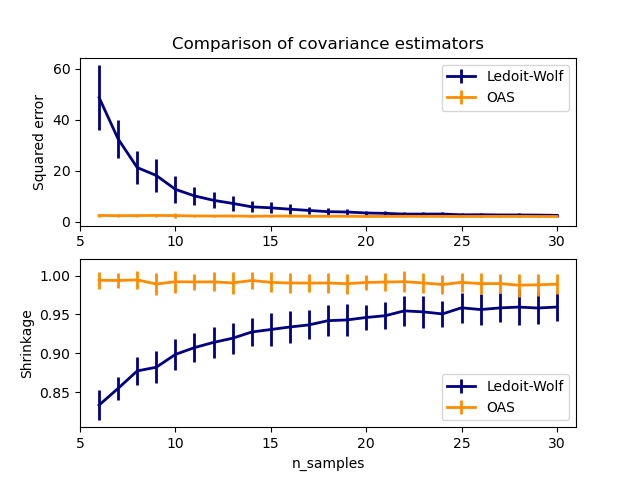
../_images/sphx_glr_plot_lw_vs_oas_001.png

2.6.3. Covarianza inversa dispersa

La matriz inversa de la matriz de covarianza, a menudo llamada matriz de precisión, es proporcional a la matriz de correlación parcial. Proporciona la relación de independencia parcial. En otras palabras, si dos características son independientes condicionalmente de las otras, el coeficiente correspondiente en la matriz de precisión será cero. Por eso tiene sentido estimar una matriz de precisión dispersa: la estimación de la matriz de covarianza está mejor condicionada por el reconocimiento de las relaciones de independencia a partir de los datos. Esto se conoce como selección de covarianza.

En la situación de muestras pequeñas, en la que n_muestras es del orden de n_caracteres o menor, los estimadores de covarianza inversa dispersa tienden a funcionar mejor que los estimadores de covarianza reducida. Sin embargo, en la situación contraria, o para datos muy correlacionados, pueden ser numéricamente inestables. Además, a diferencia de los estimadores de reducción, los estimadores dispersos son capaces de recuperar la estructura no diagonal.

El estimador GraphicalLasso utiliza una penalización l1 para imponer la dispersión en la matriz de precisión: cuanto mayor sea su parámetro alpha, más dispersa será la matriz de precisión. El objeto GraphicalLassoCV correspondiente utiliza la validación cruzada para establecer automáticamente el parámetro alpha.

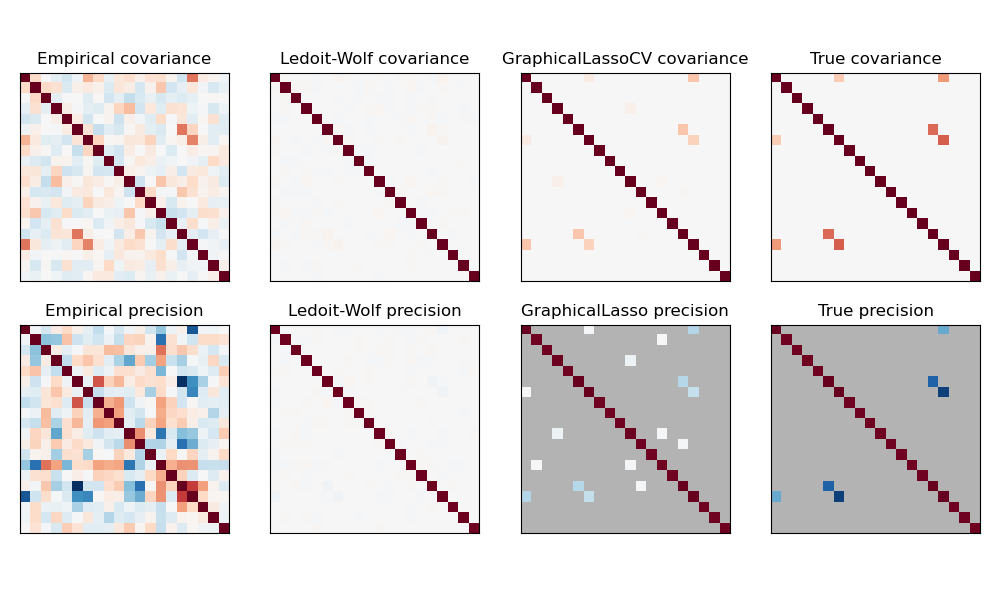
../_images/sphx_glr_plot_sparse_cov_001.png

Una comparación de las estimaciones de máxima verosimilitud, reducción y dispersión de la matriz de covarianza y precisión en las modalidades de muestras muy pequeñas.

Nota

Recuperación de la estructura

Recuperar una estructura gráfica de las correlaciones en los datos es un desafío. Si estás interesado en tal recuperación, ten en cuenta que:

  • La recuperación es más fácil a partir de una matriz de correlaciones que de una matriz de covarianza: estandariza tus observaciones antes de ejecutar GraphicalLasso

  • Si el gráfico subyacente tiene nodos con muchas más conexiones que el nodo promedio, el algoritmo perderá algunas de estas conexiones.

  • Si tu número de observaciones no es elevado en comparación con el número de aristas de tu gráfico subyacente, no lo recuperarás.

  • Incluso en condiciones favorables de recuperación, el parámetro alfa elegido por la validación cruzada (por ejemplo, utilizando el objeto GraphicalLassoCV) conducirá a seleccionar demasiadas aristas. Sin embargo, las aristas relevantes tendrán pesos más elevados que las irrelevantes.

La formulación matemática es la siguiente:

\[\hat{K} = \mathrm{argmin}_K \big( \mathrm{tr} S K - \mathrm{log} \mathrm{det} K + \alpha \|K\|_1 \big)\]

Donde \(K\) es la matriz de precisión a estimar, y \(S\) es la matriz de covarianza de la muestra. \(\|K\_1\) es la suma de los valores absolutos de los coeficientes fuera de diagonal de \(K\). El algoritmo empleado para resolver este problema es el algoritmo GLasso, del trabajo de Friedman 2008 en Biostatistics. Es el mismo algoritmo que aparece en el paquete glasso de R.

Ejemplos:

Referencias:

2.6.4. Estimación de Covarianza Robusta

Los conjuntos de datos reales suelen estar sujetos a errores de medición o de registro. También pueden aparecer observaciones regulares pero poco comunes por diversas razones. Las observaciones que son muy poco comunes se denominan valores atípicos. El estimador de la covarianza empírica y los estimadores de la covarianza reducida presentados anteriormente son muy sensibles a la presencia de valores atípicos en los datos. Por lo tanto, hay que utilizar estimadores de covarianza robustos para estimar la covarianza de sus conjuntos de datos reales. Por otra parte, los estimadores de covarianza robustos pueden utilizarse para realizar la detección de valores atípicos y descartar/reducir la ponderación de algunas observaciones de acuerdo con el procesamiento posterior de los datos.

El paquete sklearn.covariance implementa un estimador robusto de la covarianza, el Determinante Mínimo de la Covarianza 3.

2.6.4.1. Determinante Mínimo de la Covarianza

El Estimador del Determinante Mínimo de la Covarianza es un estimador robusto de la covarianza de un conjunto de datos introducido por P.J. Rousseeuw en 3. La idea es encontrar una determinada proporción (h) de observaciones «buenas» que no sean valores atípicos y calcular su matriz de covarianza empírica. Esta matriz de covarianza empírica se reescala para compensar la selección de observaciones realizada («paso de consistencia»). Una vez calculado el Estimador del Determinante Mínimo de la Covarianza, se pueden asignar pesos a las observaciones en función de su distancia de Mahalanobis, lo que conduce a una estimación reponderada de la matriz de covarianza del conjunto de datos («paso de reponderación»).

Rousseeuw y Van Driessen 4 desarrollaron el algoritmo FastMCD para calcular el Determinante de Covarianza Mínimo. Este algoritmo se utiliza en scikit-learn cuando se ajusta un objeto MCD a los datos. El algoritmo FastMCD también calcula una estimación robusta de la ubicación del conjunto de datos al mismo tiempo.

Se puede acceder a las estimaciones en bruto como atributos raw_location_ y raw_covariance_ de un objeto estimador de covarianza robusta MinCovDet.

Referencias:

3(1,2)

P. J. Rousseeuw. Least median of squares regression. J. Am Stat Ass, 79:871, 1984.

4

A Fast Algorithm for the Minimum Covariance Determinant Estimator, 1999, American Statistical Association and the American Society for Quality, TECHNOMETRICS.

Ejemplos:

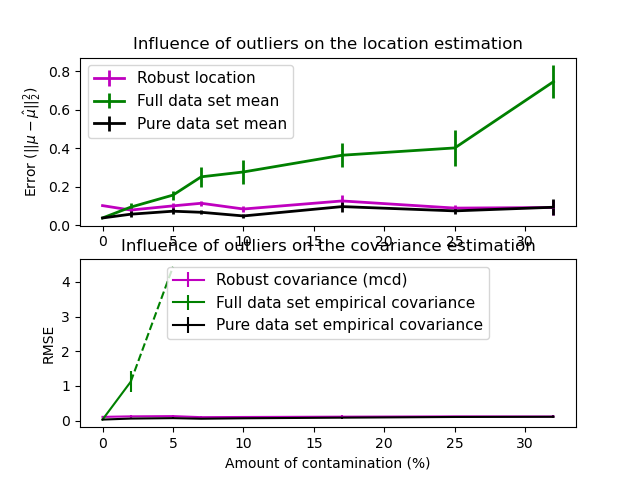
Influencia de los valores atípicos en las estimaciones de localización y covarianza

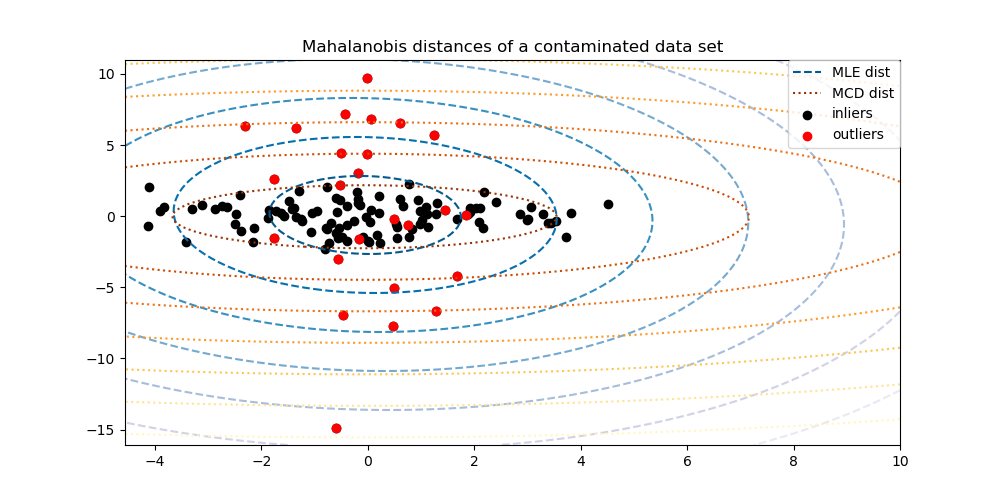
Separar valores típicos de atípicos utilizando una distancia de Mahalanobis

robust_vs_emp

mahalanobis