Estimación de la covarianza robusta frente a la empírica

La estimación habitual de la covarianza por máxima verosimilitud es muy sensible a la presencia de valores atípicos en el conjunto de datos. En tal caso, sería mejor utilizar un estimador robusto de la covarianza para garantizar que la estimación es resistente a las observaciones «erróneas» en el conjunto de datos. 1, 2

Estimador del determinante mínimo de la covarianza

El estimador del Determinante Mínimo de la Covarianza es un estimador de la covarianza robusto y de alto punto de ruptura (es decir, puede utilizarse para estimar la matriz de covarianza de conjuntos de datos muy contaminados, hasta \(\frac{n_\text{samples} - n_\text{features}-1}{2}\) los valores atípicos). La idea es encontrar \(\frac{n_\text{samples} + n_\text{features}+1}{2}\) observaciones cuya covarianza empírica tiene el menor determinante, dando lugar a un subconjunto «puro» de observaciones a partir del cual calcular las estimaciones estándar de ubicación y covarianza. Después de un paso de corrección destinado a compensar el hecho de que las estimaciones se aprendieron a partir de sólo una parte de los datos iniciales, terminamos con estimaciones robustas de la ubicación y la covarianza del conjunto de datos.

El estimador del Determinante de Covarianza Mínimo (MCD) ha sido introducido por P.J.Rousseuw en 3.

Evaluación

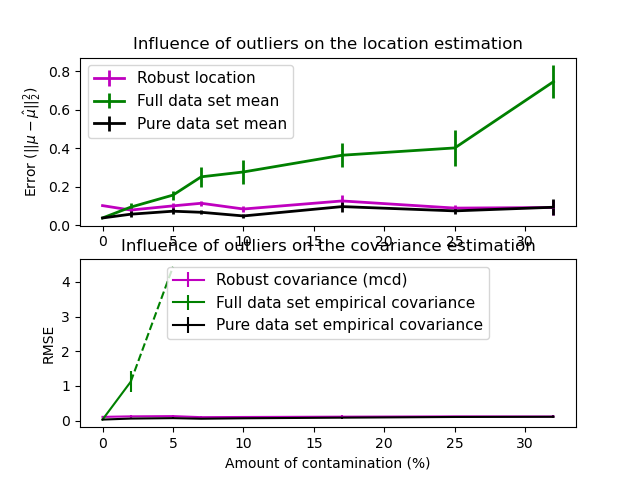
En este ejemplo, comparamos los errores de estimación que se cometen al utilizar varios tipos de estimaciones de localización y covarianza en conjuntos de datos distribuidos gaussianos contaminados:

• La media y la covarianza empírica del conjunto de datos, que se rompen en cuanto hay valores atípicos en el conjunto de datos

• El MCD robusto, que tiene un bajo error siempre que \(n_\text{samples} > 5n_\text{features}\)

• La media y la covarianza empírica de las observaciones que se sabe que son buenas. Esto puede considerarse como una estimación «perfecta» del MCD, por lo que se puede confiar en nuestra aplicación comparándola con este caso.

Referencias

1

Johanna Hardin, David M Rocke. The distribution of robust distances. Journal of Computational and Graphical Statistics. December 1, 2005, 14(4): 928-946.

2

Zoubir A., Koivunen V., Chakhchoukh Y. and Muma M. (2012). Robust estimation in signal processing: A tutorial-style treatment of fundamental concepts. IEEE Signal Processing Magazine 29(4), 61-80.

3

P. J. Rousseeuw. Least median of squares regression. Journal of American Statistical Ass., 79:871, 1984.

print(__doc__)

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.font_manager

from sklearn.covariance import EmpiricalCovariance, MinCovDet

# example settings
n_samples = 80
n_features = 5
repeat = 10

range_n_outliers = np.concatenate(
    (np.linspace(0, n_samples / 8, 5),
     np.linspace(n_samples / 8, n_samples / 2, 5)[1:-1])).astype(int)

# definition of arrays to store results
err_loc_mcd = np.zeros((range_n_outliers.size, repeat))
err_cov_mcd = np.zeros((range_n_outliers.size, repeat))
err_loc_emp_full = np.zeros((range_n_outliers.size, repeat))
err_cov_emp_full = np.zeros((range_n_outliers.size, repeat))
err_loc_emp_pure = np.zeros((range_n_outliers.size, repeat))
err_cov_emp_pure = np.zeros((range_n_outliers.size, repeat))

# computation
for i, n_outliers in enumerate(range_n_outliers):
    for j in range(repeat):

        rng = np.random.RandomState(i * j)

        # generate data
        X = rng.randn(n_samples, n_features)
        # add some outliers
        outliers_index = rng.permutation(n_samples)[:n_outliers]
        outliers_offset = 10. * \
            (np.random.randint(2, size=(n_outliers, n_features)) - 0.5)
        X[outliers_index] += outliers_offset
        inliers_mask = np.ones(n_samples).astype(bool)
        inliers_mask[outliers_index] = False

        # fit a Minimum Covariance Determinant (MCD) robust estimator to data
        mcd = MinCovDet().fit(X)
        # compare raw robust estimates with the true location and covariance
        err_loc_mcd[i, j] = np.sum(mcd.location_ ** 2)
        err_cov_mcd[i, j] = mcd.error_norm(np.eye(n_features))

        # compare estimators learned from the full data set with true
        # parameters
        err_loc_emp_full[i, j] = np.sum(X.mean(0) ** 2)
        err_cov_emp_full[i, j] = EmpiricalCovariance().fit(X).error_norm(
            np.eye(n_features))

        # compare with an empirical covariance learned from a pure data set
        # (i.e. "perfect" mcd)
        pure_X = X[inliers_mask]
        pure_location = pure_X.mean(0)
        pure_emp_cov = EmpiricalCovariance().fit(pure_X)
        err_loc_emp_pure[i, j] = np.sum(pure_location ** 2)
        err_cov_emp_pure[i, j] = pure_emp_cov.error_norm(np.eye(n_features))

# Display results
font_prop = matplotlib.font_manager.FontProperties(size=11)
plt.subplot(2, 1, 1)
lw = 2
plt.errorbar(range_n_outliers, err_loc_mcd.mean(1),
             yerr=err_loc_mcd.std(1) / np.sqrt(repeat),
             label="Robust location", lw=lw, color='m')
plt.errorbar(range_n_outliers, err_loc_emp_full.mean(1),
             yerr=err_loc_emp_full.std(1) / np.sqrt(repeat),
             label="Full data set mean", lw=lw, color='green')
plt.errorbar(range_n_outliers, err_loc_emp_pure.mean(1),
             yerr=err_loc_emp_pure.std(1) / np.sqrt(repeat),
             label="Pure data set mean", lw=lw, color='black')
plt.title("Influence of outliers on the location estimation")
plt.ylabel(r"Error ($||\mu - \hat{\mu}||_2^2$)")
plt.legend(loc="upper left", prop=font_prop)

plt.subplot(2, 1, 2)
x_size = range_n_outliers.size
plt.errorbar(range_n_outliers, err_cov_mcd.mean(1),
             yerr=err_cov_mcd.std(1),
             label="Robust covariance (mcd)", color='m')
plt.errorbar(range_n_outliers[:(x_size // 5 + 1)],
             err_cov_emp_full.mean(1)[:(x_size // 5 + 1)],
             yerr=err_cov_emp_full.std(1)[:(x_size // 5 + 1)],
             label="Full data set empirical covariance", color='green')
plt.plot(range_n_outliers[(x_size // 5):(x_size // 2 - 1)],
         err_cov_emp_full.mean(1)[(x_size // 5):(x_size // 2 - 1)],
         color='green', ls='--')
plt.errorbar(range_n_outliers, err_cov_emp_pure.mean(1),
             yerr=err_cov_emp_pure.std(1),
             label="Pure data set empirical covariance", color='black')
plt.title("Influence of outliers on the covariance estimation")
plt.xlabel("Amount of contamination (%)")
plt.ylabel("RMSE")
plt.legend(loc="upper center", prop=font_prop)

plt.show()