Regresión por componentes principales frente a la regresión por mínimos cuadrados parciales

Este ejemplo compara la Regresión por componentes principales (PCR) y la Regresión por mínimos cuadrados parciales (PLS) en un conjunto de datos de juguete. Nuestro objetivo es ilustrar cómo PLS puede superar a PCR cuando el objetivo está fuertemente correlacionado con algunas direcciones en los datos que tienen una baja varianza.

PCR es un regresor compuesto por dos pasos: primero, se aplica PCA a los datos de entrenamiento, posiblemente realizando una reducción de la dimensionalidad; después, se entrena un regresor (por ejemplo, un regresor lineal) en las muestras transformadas. En PCA, la transformación es puramente no supervisada, lo que significa que no se utiliza información sobre los objetivos. Como resultado, la PCR puede tener un mal rendimiento en algunos conjuntos de datos en los que el objetivo está fuertemente correlacionado con direcciones que tienen baja varianza. De hecho, la reducción de la dimensionalidad de PCA proyecta los datos en un espacio de menor dimensión en el que la varianza de los datos proyectados se maximiza con avidez a lo largo de cada eje. A pesar de que tienen el mayor poder predictivo sobre el objetivo, las direcciones con una varianza más baja serán descartadas, y el regresor final no podrá aprovecharlas.

PLS es tanto un transformador como un regresor, y es bastante similar a la PCR: también aplica una reducción de la dimensionalidad a las muestras antes de aplicar un regresor lineal a los datos transformados. La principal diferencia con la PCR es que la transformación PLS es supervisada. Por lo tanto, como veremos en este ejemplo, no sufre el problema que acabamos de mencionar.

print(__doc__)

Los datos

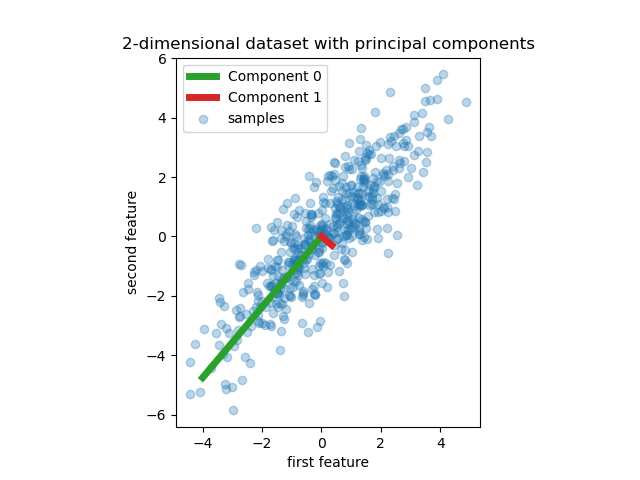
Comenzamos creando un conjunto de datos sencillo con dos características. Antes de sumergirnos en la PCR y el PLS, ajustamos un estimador PCA para mostrar los dos componentes principales de este conjunto de datos, es decir, las dos direcciones que explican la mayor parte de la varianza en los datos.

import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA

rng = np.random.RandomState(0)
n_samples = 500
cov = [[3, 3],
       [3, 4]]
X = rng.multivariate_normal(mean=[0, 0], cov=cov, size=n_samples)
pca = PCA(n_components=2).fit(X)


plt.scatter(X[:, 0], X[:, 1], alpha=.3, label='samples')
for i, (comp, var) in enumerate(zip(pca.components_, pca.explained_variance_)):
    comp = comp * var  # scale component by its variance explanation power
    plt.plot([0, comp[0]], [0, comp[1]], label=f"Component {i}", linewidth=5,
             color=f"C{i + 2}")
plt.gca().set(aspect='equal',
              title="2-dimensional dataset with principal components",
              xlabel='first feature', ylabel='second feature')
plt.legend()
plt.show()

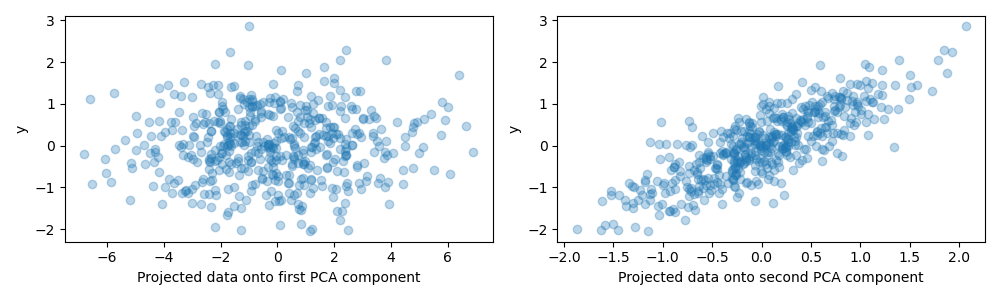
Para el propósito de este ejemplo, ahora definimos el objetivo y de manera que esté fuertemente correlacionado con una dirección que tenga una varianza pequeña. Para ello, proyectaremos X sobre la segunda componente y le añadiremos algo de ruido.

y = X.dot(pca.components_[1]) + rng.normal(size=n_samples) / 2

fig, axes = plt.subplots(1, 2, figsize=(10, 3))

axes[0].scatter(X.dot(pca.components_[0]), y, alpha=.3)
axes[0].set(xlabel='Projected data onto first PCA component', ylabel='y')
axes[1].scatter(X.dot(pca.components_[1]), y, alpha=.3)
axes[1].set(xlabel='Projected data onto second PCA component', ylabel='y')
plt.tight_layout()
plt.show()

Proyección sobre un componente y potencia de predicción

Ahora creamos dos regresores: PCR y PLS, y para nuestra ilustración fijamos el número de componentes en 1. Antes de alimentar los datos al paso PCA de PCR, primero los estandarizamos, como recomiendan las buenas prácticas. El estimador PLS tiene capacidades de escala incorporadas.

Para ambos modelos, trazamos los datos proyectados en el primer componente contra el objetivo. En ambos casos, estos datos proyectados son los que los regresores utilizarán como datos de entrenamiento.

from sklearn.model_selection import train_test_split
from sklearn.pipeline import make_pipeline
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.cross_decomposition import PLSRegression

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=rng)

pcr = make_pipeline(StandardScaler(), PCA(n_components=1), LinearRegression())
pcr.fit(X_train, y_train)
pca = pcr.named_steps['pca']  # retrieve the PCA step of the pipeline

pls = PLSRegression(n_components=1)
pls.fit(X_train, y_train)

fig, axes = plt.subplots(1, 2, figsize=(10, 3))
axes[0].scatter(pca.transform(X_test), y_test, alpha=.3, label='ground truth')
axes[0].scatter(pca.transform(X_test), pcr.predict(X_test), alpha=.3,
                label='predictions')
axes[0].set(xlabel='Projected data onto first PCA component',
            ylabel='y', title='PCR / PCA')
axes[0].legend()
axes[1].scatter(pls.transform(X_test), y_test, alpha=.3, label='ground truth')
axes[1].scatter(pls.transform(X_test), pls.predict(X_test), alpha=.3,
                label='predictions')
axes[1].set(xlabel='Projected data onto first PLS component',
            ylabel='y', title='PLS')
axes[1].legend()
plt.tight_layout()
plt.show()

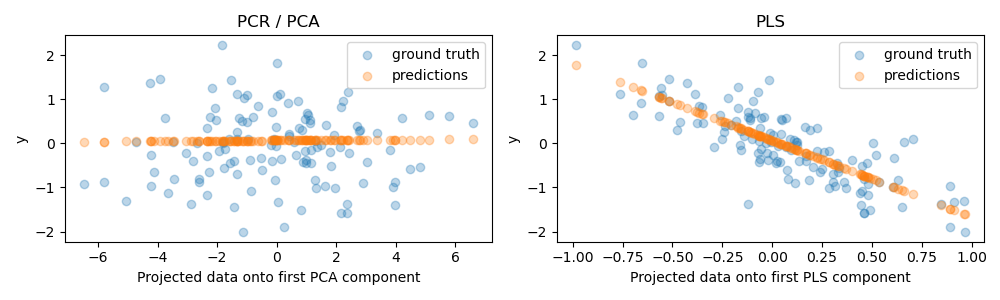
Como era de esperar, la transformación PCA no supervisada de PCR ha dejado de lado el segundo componente, es decir, la dirección con menor varianza, a pesar de ser la dirección más predictiva. Esto se debe a que el PCA es una transformación completamente no supervisada, y da lugar a que los datos proyectados tengan una baja potencia predictivo sobre el objetivo.

Por otra parte, el regresor PLS consigue captar el efecto de la dirección con menor varianza, gracias a que utiliza la información del objetivo durante la transformación: puede reconocer que esta dirección es realmente la más predictiva. Observamos que el primer componente del PLS está correlacionado negativamente con el objetivo, lo que se debe a que los signos de los autovectores son arbitrarios.

También imprimimos las puntuaciones R-cuadrado de ambos estimadores, lo que confirma aún más que PLS es una alternativa mejor que PCR en este caso. Un R-cuadrado negativo indica que la PCR funciona peor que un regresor que simplemente predice la media del objetivo.

print(f"PCR r-squared {pcr.score(X_test, y_test):.3f}")
print(f"PLS r-squared {pls.score(X_test, y_test):.3f}")

Out:

PCR r-squared -0.026
PLS r-squared 0.658

Como observación final, observamos que la PCR con 2 componentes funciona tan bien como la PLS: esto se debe a que, en este caso, la PCR pudo aprovechar el segundo componente que tiene el mayor poder de predicción sobre el objetivo.

pca_2 = make_pipeline(PCA(n_components=2), LinearRegression())
pca_2.fit(X_train, y_train)
print(f"PCR r-squared with 2 components {pca_2.score(X_test, y_test):.3f}")

Out:

PCR r-squared with 2 components 0.673