2.8. Estimación de densidad

La estimación de densidad recorre la línea entre el aprendizaje no supervisado, la ingeniería de características y el modelado de datos. Algunas de las técnicas de estimación de densidad más populares y útiles son los modelos de mezcla tales como Mezclas Gaussianas (GaussianMixture), y enfoques basados en vecinos, como la estimación de densidad del kernel (KernelDensity). Las Mezclas Gaussianas se discuten más ampliamente en el contexto de Análisis de conglomerados, porque la técnica también es útil como un esquema de análisis de conglomerados no supervisado.

La estimación de densidad es un concepto muy simple, y la mayoría de personas ya está familiarizada con una técnica común de estimación de densidad: el histograma.

2.8.1. Estimación de Densidad: Histogramas

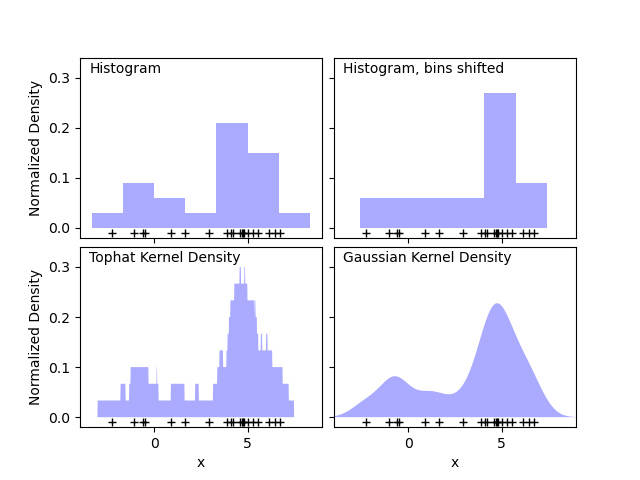
Un histograma es una visualización de datos simple donde se definen los intervalos y se cuenta el número de puntos de datos dentro de cada intervalo. Un ejemplo de un histograma puedes verlo en el panel superior izquierdo de la siguiente figura:

hist_to_kde

Sin embargo, un problema importante con los histogramas es que la elección de la agrupación de los intervalos puede tener un efecto desproporcionado en la visualización resultante. Considera el panel superior derecho de la figura anterior. Muestra un histograma sobre los mismos datos, con los intervalos desplazados a la derecha. Los resultados de las dos visualizaciones se ven completamente diferentes y pueden llevar a diferentes interpretaciones de los datos.

Intuitivamente, también se puede pensar en un histograma como una pila de bloques, un bloque por punto. Apilando los bloques en el espacio de la cuadrícula apropiado, recuperamos el histograma. ¿Pero qué pasa si, en lugar de apilar los bloques en una cuadrícula regular, centramos cada bloque en el punto que representa y sumamos la altura total en cada lugar? Esta idea conduce a la visualización de la parte inferior izquierda. Tal vez no sea tan limpia como un histograma, pero el hecho de que los datos dirijan las ubicaciones de los bloques significa que es una representación mucho mejor de los datos subyacentes.

Esta visualización es un ejemplo de estimación de la densidad del kernel, en este caso con un kernel superior estimado (es decir, un bloque cuadrado en cada punto). Podemos recuperar una distribución más suave utilizando un kernel más suave. El gráfico de abajo a la derecha muestra una estimación de la densidad del kernel Gaussiano, en la que cada punto contribuye con una curva Gaussiana al total. El resultado es una estimación de densidad suave que se deriva de los datos, y funciones como un potente modelo no paramétrico de la distribución de puntos.

2.8.2. Estimación de densidad del Kernel

La estimación de densidad del kernel en scikit-learn está implementada en el estimador KernelDensity, que utiliza el Árbol de Bolas o el Árbol KD para consultas eficientes (ver Vecino más cercano para una discusión de estos). Aunque el ejemplo anterior utiliza un conjunto de datos unidimensional por simplicidad, la estimación de densidad del kernel puede realizarse en cualquier número de dimensiones, aunque en la práctica la maldición de la dimensionalidad hace que su rendimiento se degrade en altas dimensiones altas.

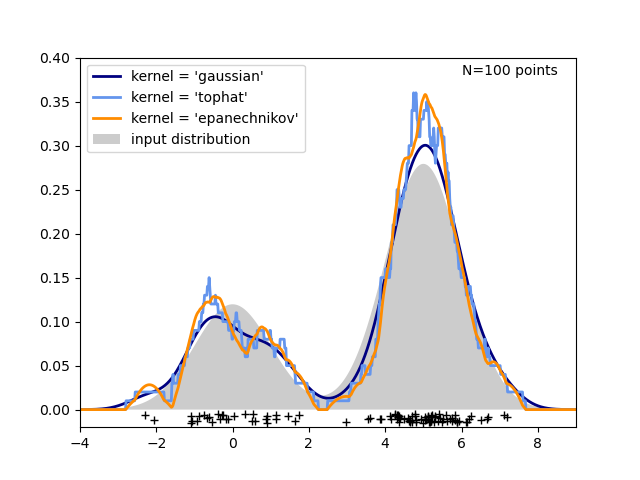
En la siguiente figura, se extraen 100 puntos de una distribución bimodal, y se muestran las estimaciones de densidad del kernel para tres opciones de kernels:

kde_1d_distribution

Está claro cómo la forma del núcleo afecta a la suavidad de la distribución resultante. El estimador de densidad del núcleo de aprendizaje de ciencia puede utilizarse de la siguiente manera:

>>> from sklearn.neighbors import KernelDensity
>>> import numpy as np
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> kde = KernelDensity(kernel='gaussian', bandwidth=0.2).fit(X)
>>> kde.score_samples(X)
array([-0.41075698, -0.41075698, -0.41076071, -0.41075698, -0.41075698,
       -0.41076071])

Aquí hemos utilizado kernel='gaussian', como has visto anteriormente. Matemáticamente, un kernel es una función positiva \(K(x;h)\) que está controlada por el parámetro de ancho de banda \(h\). Dada esta forma del kernel, la estimación de la densidad en un punto \(y\) dentro de un grupo de puntos \(x_i; i=1\cdots N\) viene dada por:

\[\rho_K(y) = \sum_{i=1}^{N} K(y - x_i; h)\]

El ancho de banda actúa aquí como un parámetro de suavización, controlando el equilibrio entre el sesgo y la varianza en el resultado. Un ancho de banda grande conduce a una distribución de densidad muy suave (es decir, de alto sesgo). Un ancho de banda pequeño conduce a una distribución de densidad poco suave (es decir, de alta varianza).

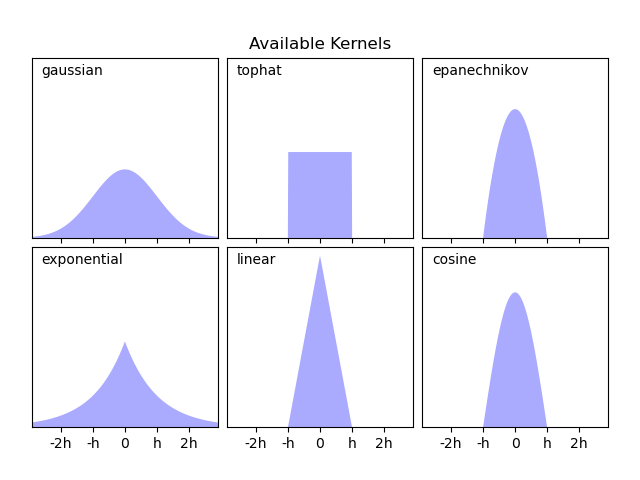
KernelDensity implementa varias formas de kernel comunes, que se muestran en la siguiente figura:

kde_kernels

La forma de estos kernels es la siguiente:

  • Kernel Gaussiano (kernel = 'gaussian')

    \(K(x; h) \propto \exp(- \frac{x^2}{2h^2} )\)

  • Kernel superior estimado (kernel = 'tophat')

    \(K(x; h) \propto 1\) if \(x < h\)

  • Kernel de Epanechnikov (kernel = 'epanechnikov')

    \(K(x; h) \propto 1 - \frac{x^2}{h^2}\)

  • Kernel exponencial (kernel = 'exponential')

    \(K(x; h) \propto \exp(-x/h)\)

  • Kernel lineal (kernel = 'linear')

    \(K(x; h) \propto 1 - x/h\) if \(x < h\)

  • Kernel del coseno (kernel = 'cosine')

    \(K(x; h) \propto \cos(\frac{\pi x}{2h})\) if \(x < h\)

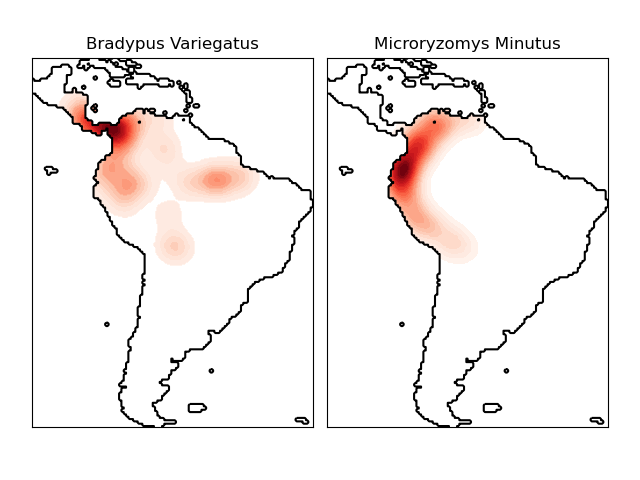
El estimador de densidad del kernel puede ser usado con cualquiera de las métricas de distancia válidas (ver DistanceMetric para una lista de métricas disponibles), aunque los resultados están normalizados adecuadamente sólo para la métrica Euclideana. Una métrica particularmente útil es la Haversine distance que mide la distancia angular entre puntos en una esfera. Aquí hay un ejemplo de uso de una estimación de densidad del kernel para una visualización de datos geoespaciales, en este caso la distribución de observaciones de dos especies diferentes en el continente sudamericano:

species_kde

Otra aplicación útil de la estimación de densidad del kernel es aprender de un modelo generativo no paramétrico de un conjunto de datos con el fin de extraer eficientemente nuevas muestras de este modelo generativo. Aquí hay un ejemplo de uso de este proceso para crear un nuevo conjunto de dígitos manuscritos, usando un kernel Gaussiano aprendido en una proyección PCA de los datos:

digits_kde

Los datos «new» consisten en combinaciones lineales de los datos de entrada, con ponderaciones extraídas probabilísticamente dado el modelo KDE.

Ejemplos: