2.9. Modelos de red neural (no supervisados)

2.9.1. Máquinas Boltzmann restringidas

Las máquinas de Boltzmann restringidas (RBM) son aprendices de características no lineales no supervisadas basadas en un modelo probabilístico. Las características extraídas por una RBM o una jerarquía de RBM suelen dar buenos resultados cuando se introducen en un clasificador lineal como una SVM lineal o un perceptrón.

El modelo hace suposiciones sobre la distribución de las entradas. Por el momento, scikit-learn sólo proporciona BernoulliRBM, que asume que las entradas son valores binarios o valores entre 0 y 1, cada uno codificando la probabilidad de que la característica específica se active.

El RBM trata de maximizar la probabilidad de los datos utilizando un modelo gráfico determinado. El algoritmo de aprendizaje de parámetros utilizado (Máxima Verosimilitud Estocástica) evita que las representaciones se alejen de los datos de entrada, lo que hace que capturen regularidades interesantes, pero hace que el modelo sea menos útil para conjuntos de datos pequeños, y normalmente no es útil para la estimación de la densidad.

El método ganó popularidad para inicializar redes neuronales profundas con los pesos de RBMs independientes. Este método se conoce como preentrenamiento no supervisado.

../_images/sphx_glr_plot_rbm_logistic_classification_001.png

Ejemplos:

2.9.1.1. Modelo gráfico y parametrización

El modelo gráfico de un RBM es un grafo bipartito completamente conectado.

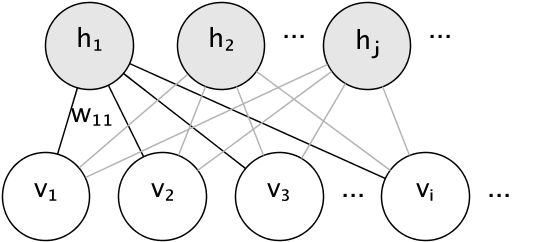
../_images/rbm_graph.png

Los nodos son variables aleatorias cuyos estados dependen del estado de los otros nodos a los que están conectados. Por lo tanto, el modelo está parametrizado por las ponderaciones de las conexiones, así como un término de intercepción (sesgo) para cada unidad visible y oculta, omitido en la imagen por simplicidad.

La función energética mide la calidad de una asignación conjunta:

\[E(\mathbf{v}, \mathbf{h}) = -\sum_i \sum_j w_{ij}v_ih_j - \sum_i b_iv_i - \sum_j c_jh_j\]

En la fórmula anterior, \(\mathbf{b}\) y \(\mathbf{c}\) son los vectores de intercepción para las capas visible y oculta, respectivamente. La probabilidad conjunta del modelo se define en términos de energía:

\[P(\mathbf{v}, \mathbf{h}) = \frac{e^{-E(\mathbf{v}, \mathbf{h})}}{Z}\]

La palabra restringida se refiere a la estructura bipartita del modelo, que prohíbe la interacción directa entre unidades ocultas, o entre unidades visibles. Esto significa que se asumen las siguientes independencias condicionales:

\[\begin{split}h_i \bot h_j | \mathbf{v} \\ v_i \bot v_j | \mathbf{h}\end{split}\]

La estructura bipartita permite el uso de un eficiente muestreo de Gibbs en bloque para la inferencia.

2.9.1.2. Máquinas de Boltzmann restringidas de Bernoulli

En la BernoulliRBM, todas las unidades son unidades estocásticas binarias. Esto significa que los datos de entrada deben ser binarios, o de valor real entre 0 y 1, lo que significa la probabilidad de que la unidad visible se encienda o se apague. Este es un buen modelo para el reconocimiento de caracteres, donde el interés está en qué píxeles están activos y cuáles no. Para las imágenes de escenas naturales ya no se ajusta debido al fondo, la profundidad y la tendencia de los píxeles vecinos a tomar los mismos valores.

La distribución de probabilidad condicional de cada unidad viene dada por la función de activación sigmoidal logística de la entrada que recibe:

\[\begin{split}P(v_i=1|\mathbf{h}) = \sigma(\sum_j w_{ij}h_j + b_i) \\ P(h_i=1|\mathbf{v}) = \sigma(\sum_i w_{ij}v_i + c_j)\end{split}\]

donde \(\sigma\) es la función sigmoidal logística:

\[\sigma(x) = \frac{1}{1 + e^{-x}}\]

2.9.1.3. Aprendizaje por máxima verosimilitud estocástica

El algoritmo de entrenamiento implementado en BernoulliRBM se conoce como Máxima Verosimilitud Estocástica (SML) o Divergencia Contrastiva Persistente (PCD). Optimizar la máxima verosimilitud directamente es inviable debido a la forma de la verosimilitud de los datos:

\[\log P(v) = \log \sum_h e^{-E(v, h)} - \log \sum_{x, y} e^{-E(x, y)}\]

Para simplificar, la ecuación anterior está escrita para un solo ejemplo de entrenamiento. El gradiente con respecto a los pesos está formado por dos términos correspondientes a los anteriores. Suelen conocerse como gradiente positivo y gradiente negativo, por sus respectivos signos. En esta implementación, los gradientes se estiman sobre mini-lotes de muestras.

Al maximizar el logaritmo de la verosimilitud, el gradiente positivo hace que el modelo prefiera los estados ocultos que son compatibles con los datos de entrenamiento observados. Debido a la estructura bipartita de los RBM, puede calcularse de forma eficiente. El gradiente negativo, sin embargo, es inmanejable. Su objetivo es reducir la energía de los estados conjuntos que el modelo prefiere, haciendo que se mantenga fiel a los datos. Puede aproximarse mediante el Monte Carlo de cadenas de Markov utilizando el muestreo de Gibbs en bloque, muestreando iterativamente cada uno de los \(v\) y \(h\) dado el otro, hasta que la cadena se mezcle. Las muestras generadas de este modo se denominan a veces partículas de fantasía. Esto es ineficiente y es difícil determinar si la cadena de Markov se mezcla.

El método de Divergencia Contrastiva sugiere detener la cadena después de un pequeño número de iteraciones, \(k\), por lo general hasta 1. Este método es rápido y tiene una baja varianza, pero las muestras están lejos de la distribución del modelo.

La Divergencia Contrastiva Persistente aborda esta cuestión. En lugar de iniciar una nueva cadena cada vez que se necesita el gradiente, y realizar sólo un paso de muestreo de Gibbs, en la PCD mantenemos un número de cadenas (partículas de fantasía) que se actualizan \(k\) pasos de Gibbs después de cada actualización de ponderaciones. Esto permite que las partículas exploren el espacio más a fondo.

Referencias: