1.6. Vecino más cercano

sklearn.neighbors proporciona funcionalidad para métodos de aprendizaje basados en vecinos no supervisados y supervisados. Los vecinos más cercanos no supervisados son la base de muchos otros métodos de aprendizaje, especialmente el aprendizaje múltiple y la agrupación espectral. El aprendizaje basado en vecinos supervisados tiene dos variantes: classification para datos con etiquetas discretas, y regression para datos con etiquetas continuas.

El principio en el que se basan los métodos del vecino más cercano es encontrar un número predefinido de muestras de entrenamiento más cercanas en distancia al nuevo punto, y predecir la etiqueta a partir de ellas. El número de muestras puede ser una constante definida por el usuario (aprendizaje del k vecino más cercano), o variar en función de la densidad local de puntos (aprendizaje del vecino basado en el radio). La distancia puede ser, en general, cualquier medida métrica: la distancia euclidiana estándar es la opción más común. Los métodos basados en los vecinos se conocen como métodos de aprendizaje automático no generalizadores, ya que simplemente «recuerdan» todos sus datos de entrenamiento (posiblemente transformados en una estructura de indexación rápida como un Árbol de bolas o un Árbol KD).

A pesar de su simplicidad, los vecinos más cercanos han tenido éxito en un gran número de problemas de clasificación y regresión, incluyendo dígitos escritos a mano y escenas de imágenes de satélite. Al ser un método no paramétrico, suele tener éxito en situaciones de clasificación en las que el límite de decisión es muy irregular.

Las clases de sklearn.neighbors pueden manejar matrices NumPy o matrices scipy.sparse como entrada. En el caso de las matrices densas, se admite un gran número de métricas de distancia posibles. Para matrices dispersas, se admiten métricas de Minkowski arbitrarias para las búsquedas.

Hay muchas rutinas de aprendizaje que se basan en los vecinos más cercanos. Un ejemplo es kernel density estimation, discutido en la sección density estimation.

1.6.1. Vecinos más cercanos no supervisados

NearestNeighbors implementa el aprendizaje no supervisado de los vecinos más cercanos. Actúa como una interfaz uniforme para tres algoritmos diferentes de vecinos más cercanos: BallTree, KDTree, y un algoritmo de fuerza bruta basado en las rutinas de sklearn.metrics.pairwise. La elección del algoritmo de búsqueda de vecinos se controla a través de la palabra clave 'algorithm', que debe ser uno de ['auto', 'ball_tree', 'kd_tree', 'brute']. Cuando se pasa el valor por defecto 'auto', el algoritmo intenta determinar la mejor aproximación a partir de los datos de entrenamiento. Para una discusión de los puntos fuertes y débiles de cada opción, consulta Nearest Neighbor Algorithms.

Advertencia

En cuanto a los algoritmos de vecinos más cercanos, si dos vecinos \(k+1\) y \(k\) tienen distancias idénticas pero etiquetas diferentes, el resultado dependerá del orden de los datos de entrenamiento.

1.6.1.1. Encontrar a los vecinos más cercanos

Para la sencilla tarea de encontrar los vecinos más cercanos entre dos conjuntos de datos, se pueden utilizar los algoritmos no supervisados de sklearn.neighbors:

>>> from sklearn.neighbors import NearestNeighbors
>>> import numpy as np
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> nbrs = NearestNeighbors(n_neighbors=2, algorithm='ball_tree').fit(X)
>>> distances, indices = nbrs.kneighbors(X)
>>> indices
array([[0, 1],
       [1, 0],
       [2, 1],
       [3, 4],
       [4, 3],
       [5, 4]]...)
>>> distances
array([[0.        , 1.        ],
       [0.        , 1.        ],
       [0.        , 1.41421356],
       [0.        , 1.        ],
       [0.        , 1.        ],
       [0.        , 1.41421356]])

Como el conjunto de consulta se corresponde con el conjunto de entrenamiento, el vecino más cercano de cada punto es el propio punto, a una distancia de cero.

También es posible producir eficazmente un gráfico disperso que muestre las conexiones entre los puntos vecinos:

>>> nbrs.kneighbors_graph(X).toarray()
array([[1., 1., 0., 0., 0., 0.],
       [1., 1., 0., 0., 0., 0.],
       [0., 1., 1., 0., 0., 0.],
       [0., 0., 0., 1., 1., 0.],
       [0., 0., 0., 1., 1., 0.],
       [0., 0., 0., 0., 1., 1.]])

El conjunto de datos está estructurado de manera que los puntos cercanos en el orden de los índices están cerca en el espacio de los parámetros, lo que conduce a una matriz aproximadamente diagonal de bloques de los vecinos más cercanos. Este gráfico disperso es útil en una variedad de circunstancias que hacen uso de las relaciones espaciales entre los puntos para el aprendizaje no supervisado: en particular, véase Isomap, LocallyLinearEmbedding, y SpectralClustering.

1.6.1.2. Clases de árbol KD y árbol de bolas

Como alternativa, se pueden utilizar las clases KDTree o BallTree directamente para encontrar los vecinos más cercanos. Esta es la funcionalidad que envuelve la clase NearestNeighbors utilizada anteriormente. El árbol de bolas y el árbol KD tienen la misma interfaz; aquí mostraremos un ejemplo de uso del árbol KD:

>>> from sklearn.neighbors import KDTree
>>> import numpy as np
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> kdt = KDTree(X, leaf_size=30, metric='euclidean')
>>> kdt.query(X, k=2, return_distance=False)
array([[0, 1],
       [1, 0],
       [2, 1],
       [3, 4],
       [4, 3],
       [5, 4]]...)

Consulta la documentación de las clases KDTree y BallTree para obtener más información sobre las opciones disponibles para las búsquedas de vecinos más cercanos, incluyendo la especificación de estrategias de consulta, métricas de distancia, etc. Para una lista de métricas disponibles, consulta la documentación de la clase DistanceMetric.

1.6.2. Clasificación de los vecinos más cercanos

La clasificación basada en vecinos es un tipo de aprendizaje basado en instancias o aprendizaje no generalizador: no intenta construir un modelo interno general, sino que simplemente almacena instancias de los datos de entrenamiento. La clasificación se calcula a partir de una simple mayoría de votos de los vecinos más cercanos de cada punto: a un punto de consulta se le asigna la clase de datos que tiene más representantes dentro de los vecinos más cercanos del punto.

scikit-learn implementa dos clasificadores diferentes de vecinos más cercanos: KNeighborsClassifier implementa el aprendizaje basado en los \(k\) vecinos más cercanos de cada punto de consulta, donde \(k\) es un valor entero especificado por el usuario. RadiusNeighborsClassifier implementa el aprendizaje basado en el número de vecinos dentro de un radio fijo \(r\) de cada punto de entrenamiento, donde \(r\) es un valor de punto flotante especificado por el usuario.

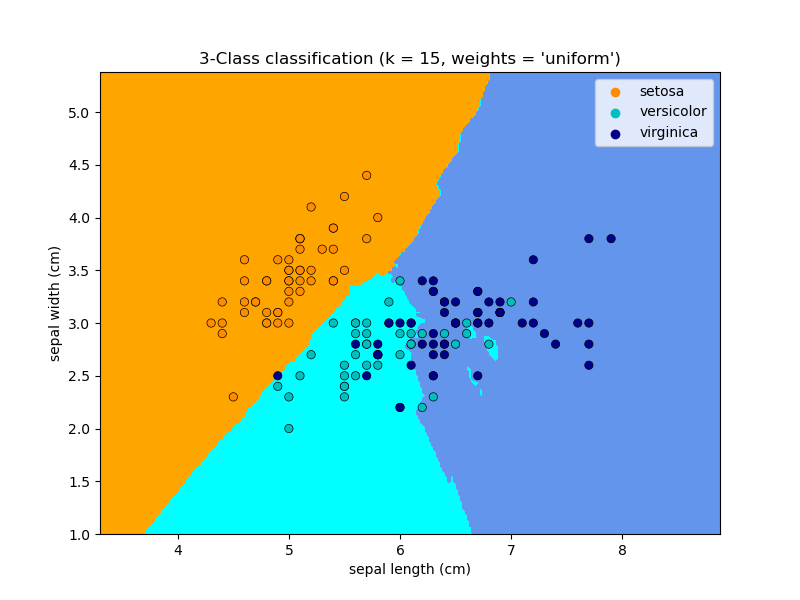
La clasificación \(k\)-neighbors en KNeighborsClassifier es la técnica más utilizada. La elección óptima del valor \(k\) depende en gran medida de los datos: en general, un \(k\) mayor suprime los efectos del ruido, pero hace que los límites de la clasificación sean menos nítidos.

En los casos en los que los datos no están muestreados uniformemente, la clasificación de vecinos basada en el radio en RadiusNeighborsClassifier puede ser una mejor opción. El usuario especifica un radio fijo \(r\), de forma que los puntos de los vecindarios más dispersos utilizan menos vecinos más cercanos para la clasificación. Para los espacios de parámetros de alta dimensión, este método se vuelve menos eficaz debido a la llamada «maldición de la dimensión».

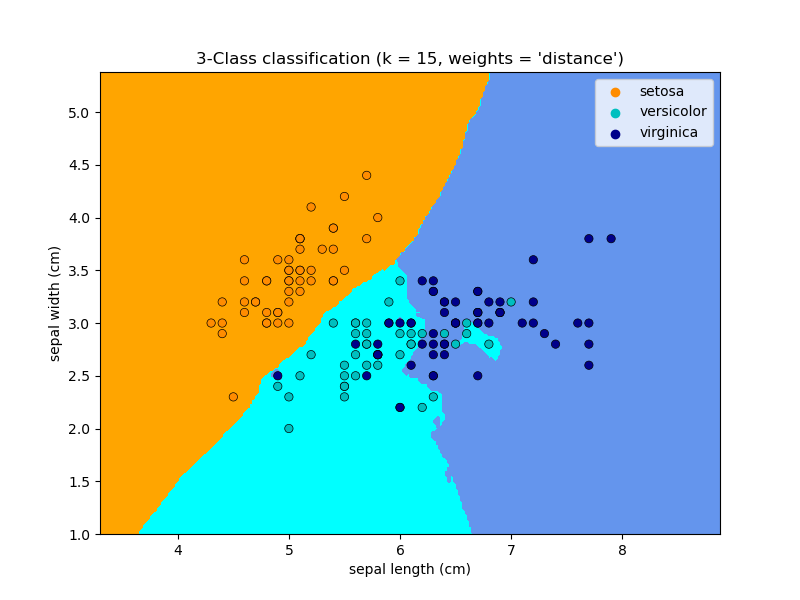
La clasificación básica de vecinos más cercanos utiliza ponderaciones uniformes: es decir, el valor asignado a un punto de consulta se calcula a partir de un voto mayoritario simple de los vecinos más cercanos. En algunas circunstancias, es mejor ponderar los vecinos de forma que los más cercanos contribuyan más al ajuste. Esto puede lograrse mediante la palabra clave weights. El valor por defecto, weights = 'uniform', asigna pesos uniformes a cada vecino. El valor weights = 'distance asigna pesos proporcionales a la inversa de la distancia al punto de consulta. Alternativamente, se puede proporcionar una función definida por el usuario de la distancia para calcular los pesos.

classification_1 classification_2

Ejemplos:

1.6.3. Regresión de vecinos más cercanos

La regresión basada en los vecinos puede utilizarse en los casos en que las etiquetas de los datos son variables continuas y no discretas. La etiqueta asignada a un punto de consulta se calcula a partir de la media de las etiquetas de sus vecinos más cercanos.

scikit-learn implementa dos regresores de vecinos diferentes: KNeighborsRegressor implementa el aprendizaje basado en los \(k\) vecinos más cercanos de cada punto de consulta, donde \(k\) es un valor entero especificado por el usuario. RadiusNeighborsRegressor implementa el aprendizaje basado en los vecinos dentro de un radio fijo \(r\) del punto de consulta, donde \(r\) es un valor de punto flotante especificado por el usuario.

La regresión básica de vecinos más cercanos utiliza pesos uniformes: es decir, cada punto del vecindario local contribuye uniformemente a la clasificación de un punto de consulta. En algunas circunstancias, puede ser ventajoso ponderar los puntos de manera que los puntos cercanos contribuyan más a la regresión que los puntos lejanos. Esto puede lograrse mediante la palabra clave weights. El valor por defecto, weights = 'uniform', asigna pesos iguales a todos los puntos. El valor weights = 'distance' asigna pesos proporcionales a la inversa de la distancia al punto de consulta. Alternativamente, se puede proporcionar una función definida por el usuario de la distancia, que se utilizará para calcular los pesos.

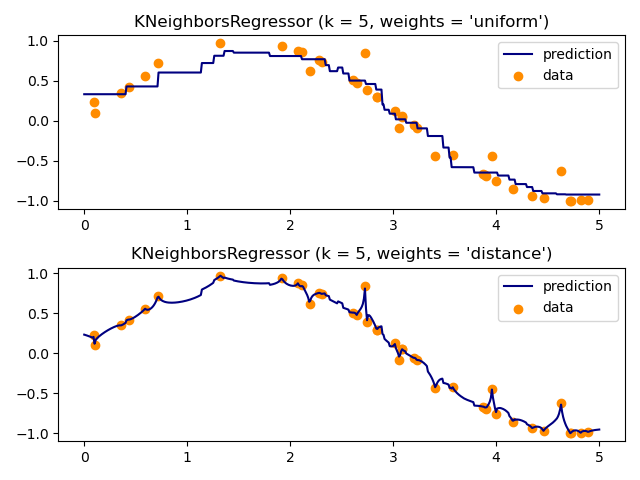
../_images/sphx_glr_plot_regression_001.png

El uso de vecinos más cercanos de salida múltiple para la regresión se demuestra en Finalización facial con estimadores de salida múltiple. En este ejemplo, las entradas X son los píxeles de la mitad superior de las caras y las salidas Y son los píxeles de la mitad inferior de esas caras.

../_images/sphx_glr_plot_multioutput_face_completion_001.png

Ejemplos:

1.6.4. Algoritmos del vecino más cercano

1.6.4.1. Fuerza bruta

El cálculo rápido de los vecinos más cercanos es un área activa de investigación en el aprendizaje automático. La implementación más simple de la búsqueda de vecinos implica el cálculo por fuerza bruta de las distancias entre todos los pares de puntos del conjunto de datos: para \(N\) muestras en \(D\) dimensiones, este enfoque se escala como \(O[D N^2]\). La búsqueda eficiente de vecinos por fuerza bruta puede ser muy competitiva para muestras de datos pequeñas. Sin embargo, a medida que el número de muestras \(N\) crece, el enfoque de fuerza bruta se vuelve rápidamente inviable. En las clases dentro de sklearn.neighbors, las búsquedas de vecinos por fuerza bruta se especifican utilizando la palabra clave algoritmo = 'brute', y se calculan utilizando las rutinas disponibles en sklearn.metrics.pairwise.

1.6.4.2. Árbol K-D

Para hacer frente a las ineficiencias computacionales del enfoque de fuerza bruta, se han inventado diversas estructuras de datos basadas en árboles. En general, estas estructuras intentan reducir el número de cálculos de distancia necesarios codificando de forma eficiente la información de distancia agregada para la muestra. La idea básica es que si el punto \(A\) está muy distante del punto \(B\), y el punto \(B\) está muy cerca del punto \(C\), entonces sabemos que los puntos \(A\) y \(C\) están muy distantes, sin tener que calcular explícitamente su distancia. De este modo, el coste computacional de una búsqueda de vecinos más cercanos puede reducirse a \(O[D N \log(N)]\) o mejor. Esto supone una mejora significativa respecto a la fuerza bruta para grandes \(N\).

Uno de los primeros enfoques para aprovechar esta información agregada fue la estructura de datos de KD tree o árbol KD (abreviatura de árbol K-dimensional), que generaliza los árboles Quad (Quad-trees) bidimensionales y los árboles Oct (Oct-trees) tridimensionales a un número arbitrario de dimensiones. El árbol KD es una estructura de árbol binario que particiona recursivamente el espacio de los parámetros a lo largo de los ejes de los datos, dividiéndolo en regiones ortotrópicas anidadas en las que se archivan los puntos de datos. La construcción de un árbol KD es muy rápida: como la partición se realiza sólo a lo largo de los ejes de datos, no es necesario calcular distancias \(D\)-dimensionales. Una vez construido, el vecino más cercano de un punto de consulta puede determinarse con sólo cálculos de distancia \(O[\log(N)]\). Aunque el enfoque del árbol KD es muy rápido para búsquedas de vecinos de baja dimensión (\(D < 20\)), se vuelve ineficiente a medida que \(D\) aumenta: esta es una manifestación de la llamada «maldición de la dimensionalidad». En scikit-learn, las búsquedas de vecinos en el árbol KD se especifican utilizando la palabra clave algoritmo = 'kd_tree', y se calculan utilizando la clase KDTree.

Referencias:

1.6.4.3. Árbol de bolas

Para hacer frente a las ineficiencias de los árboles KD en dimensiones superiores, se desarrolló la estructura de datos árbol de bolas. Mientras que los árboles KD dividen los datos a lo largo de ejes cartesianos, los árboles de bolas dividen los datos en una serie de hiperesferas anidadas. Esto hace que la construcción del árbol sea más costosa que la del árbol KD, pero da como resultado una estructura de datos que puede ser muy eficiente en datos altamente estructurados, incluso en dimensiones muy altas.

Un árbol de bolas divide recursivamente los datos en nodos definidos por un centroide \(C\) y un radio \(r\), de forma que cada punto del nodo se encuentra dentro de la hiperesfera definida por \(r\) y \(C\). El número de puntos candidatos para la búsqueda de vecinos se reduce mediante el uso de la desigualdad triangular:

\[|x+y| \leq |x| + |y|\]

Con esta configuración, un único cálculo de la distancia entre un punto de prueba y el centroide es suficiente para determinar un límite inferior y superior de la distancia a todos los puntos dentro del nodo. Debido a la geometría esférica de los nodos del árbol de bolas, puede superar a un árbol KD en dimensiones altas, aunque el rendimiento real depende en gran medida de la estructura de los datos de entrenamiento. En scikit-learn, las búsquedas de vecinos basadas en el árbol de bolas se especifican utilizando la palabra clave algoritmo = 'ball_tree', y se calculan utilizando la clase BallTree. Alternativamente, el usuario puede trabajar con la clase BallTree directamente.

Referencias:

1.6.4.4. Selección del algoritmo de los vecinos más cercanos

El algoritmo óptimo para un conjunto de datos determinado es una elección complicada y depende de varios factores:

  • número de muestras \(N\) (es decir, n_muestras) y dimensionalidad \(D\) (es decir, n_características).

    • El tiempo de consulta de fuerza bruta crece como \(O[D N]\)

    • *El tiempo de consulta del árbol de bolas crece aproximadamente como \(O[D \log(N)]\)

    • *El tiempo de consulta del árbol KD cambia con \(D\) de una manera que es difícil de caracterizar con precisión. Para \(D\) pequeños (menos de 20 aproximadamente) el costo es aproximadamente \(O[D\log(N)]\), y la consulta del árbol KD puede ser muy eficiente. Para \(D\) más grandes, el costo aumenta hasta casi \(O[DN]\), y la sobrecarga debida a la estructura de árbol puede llevar a consultas más lentas que la fuerza bruta.

    Para conjuntos de datos pequeños (\(N\) menos de 30 aproximadamente), \(log(N)\) es comparable a \(N\), y los algoritmos de fuerza bruta pueden ser más eficientes que un enfoque basado en árboles. Tanto KDTree como BallTree abordan esta cuestión proporcionando un parámetro de tamaño de hoja: éste controla el número de muestras a partir del cual una consulta pasa a ser de fuerza bruta. Esto permite que ambos algoritmos se aproximen a la eficiencia de un cálculo de fuerza bruta para un \(N\) pequeño.

  • estructura de los datos: La dimensionalidad intrínseca de los datos y/o la especificidad de los datos. La dimensionalidad intrínseca se refiere a la dimensión \(d \le D\) de un colector en el que se encuentran los datos, que puede estar incrustado de forma lineal o no lineal en el espacio de parámetros. La dispersión se refiere al grado en que los datos llenan el espacio de parámetros (esto debe distinguirse del concepto utilizado en las matrices «dispersas». La matriz de datos puede no tener entradas nulas, pero la estructura puede seguir siendo «dispersa» en este sentido).

    • El tiempo de consulta de fuerza bruta no se ve afectado por la estructura de datos.

    • Los tiempos de consulta del árbol de bolas y del árbol KD pueden verse muy influidos por la estructura de los datos. En general, los datos más dispersos con una menor dimensionalidad intrínseca conducen a tiempos de consulta más rápidos. Dado que la representación interna del árbol KD está alineada con los ejes de los parámetros, en general no mostrará tantas mejoras como el árbol de bolas para datos estructurados de forma arbitraria.

    Los conjuntos de datos utilizados en el aprendizaje automático suelen estar muy estructurados y son muy adecuados para las consultas basadas en árboles.

  • número de vecinos \(k\) solicitados para un punto de consulta.

    • *El tiempo de consulta por fuerza bruta no se ve afectado por el valor de \(k\)

    • El tiempo de consulta del árbol de bolas y del árbol KD será más lento a medida que \(k\) aumente. Esto se debe a dos efectos: en primer lugar, un \(k\) mayor conduce a la necesidad de buscar una porción mayor del espacio de parámetros. En segundo lugar, el uso de \(k > 1\) requiere la puesta en cola interna de los resultados a medida que se recorre el árbol.

    A medida que \(k\) se hace grande en comparación con \(N\), la capacidad de podar ramas en una consulta basada en un árbol se reduce. En esta situación, las consultas de fuerza bruta pueden ser más eficientes.

  • número de puntos de consulta. Tanto el árbol de bolas como el árbol KD requieren una fase de construcción. El coste de esta construcción resulta insignificante cuando se amortiza en muchas consultas. Sin embargo, si sólo se va a realizar un pequeño número de consultas, la construcción puede suponer una fracción significativa del coste total. Si se necesitan muy pocos puntos de consulta, la fuerza bruta es mejor que un método basado en árboles.

Actualmente, algorithm = 'auto' selecciona 'brute' si se verifica alguna de las siguientes condiciones:

  • los datos de entrada son dispersos

  • metric = 'precomputed'

  • \(D > 15\)

  • \(k >= N/2\)

  • effective_metric_ no está en la lista VALID_METRICS para 'kd_tree' o 'ball_tree'

En caso contrario, selecciona el primero de 'kd_tree' y 'ball_tree' que tenga effective_metric_ en su lista VALID_METRICS. Esta heurística se basa en las siguientes suposiciones:

  • el número de puntos de consulta es al menos del mismo orden que el número de puntos de entrenamiento

  • leaf_size está cerca de su valor por defecto de 30

  • cuando \(D > 15\), la dimensionalidad intrínseca de los datos es generalmente demasiado alta para los métodos basados en árboles

1.6.4.5. Efecto de leaf_size

Como se ha mencionado anteriormente, para tamaños de muestra pequeños, una búsqueda de fuerza bruta puede ser más eficiente que una consulta basada en un árbol. Este hecho se tiene en cuenta en el árbol de bolas y en el árbol KD cambiando internamente a búsquedas de fuerza bruta dentro de los nodos hoja. El nivel de este cambio puede especificarse con el parámetro leaf_size. La elección de este parámetro tiene muchos efectos:

tiempo de construcción

Un leaf_size mayor acelera el tiempo de construcción del árbol, ya que hay que crear menos nodos

tiempo de consulta

Tanto un leaf_size grande como pequeño puede llevar a un coste de consulta subóptimo. Si leaf_size se aproxima a 1, la sobrecarga que supone recorrer los nodos puede ralentizar considerablemente los tiempos de consulta. Si el tamaño de las hojas se aproxima al tamaño del conjunto de entrenamiento, las consultas se convierten en fuerza bruta. Un buen compromiso entre ambos es leaf_size = 30, el valor por defecto del parámetro.

memoria

A medida que leaf_size aumenta, la memoria requerida para almacenar una estructura de árbol disminuye. Esto es especialmente importante en el caso del árbol de bolas, que almacena un \(D\)-dimensional centroid para cada nodo. El espacio de almacenamiento requerido para BallTree es aproximadamente 1 / leaf_size el tamaño del conjunto de entrenamiento.

leaf_size no está referenciado para consultas de fuerza bruta.

1.6.5. Clasificador de centroides más cercano

El clasificador NearestCentroid es un algoritmo simple que representa cada clase por el centroide de sus miembros. En efecto, esto lo hace similar a la fase de actualización de etiquetas del algoritmo KMeans. Tampoco hay que elegir parámetros, lo que lo convierte en un buen clasificador de referencia. Sin embargo, sufre en clases no convexas, así como cuando las clases tienen varianzas drásticamente diferentes, ya que se asume una varianza igual en todas las dimensiones. Consulta Linear Discriminant Analysis (LinearDiscriminantAnalysis) y Quadratic Discriminant Analysis (QuadraticDiscriminantAnalysis) para métodos más complejos que no hacen esta suposición. El uso de la clase NearestCentroid por defecto es sencillo:

>>> from sklearn.neighbors import NearestCentroid
>>> import numpy as np
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> y = np.array([1, 1, 1, 2, 2, 2])
>>> clf = NearestCentroid()
>>> clf.fit(X, y)
NearestCentroid()
>>> print(clf.predict([[-0.8, -1]]))
[1]

1.6.5.1. Centroide de Shrunken más cercano

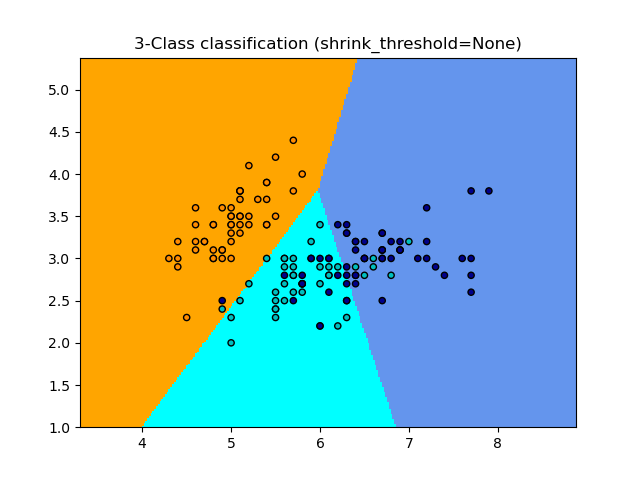
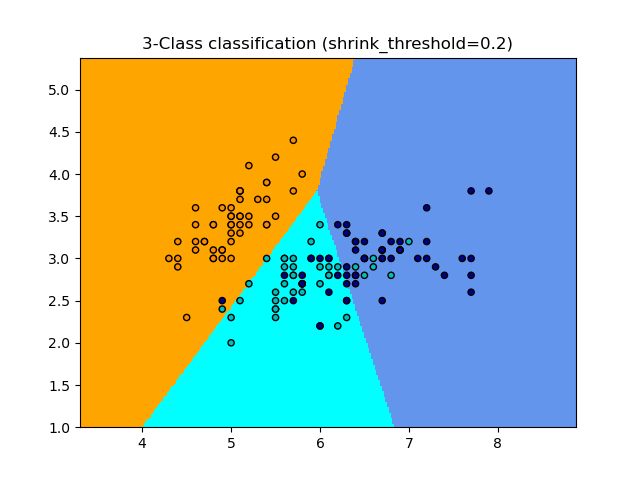
El clasificador NearestCentroid tiene un parámetro shrink_threshold, que implementa el clasificador shrunken centroid más cercano. En efecto, el valor de cada característica para cada centroide se divide por la varianza dentro de la clase de esa característica. A continuación, los valores de las características se reducen en shrink_threshold. En particular, si el valor de una característica particular es cero, se pone a cero. En efecto, esto hace que la característica no afecte a la clasificación. Esto es útil, por ejemplo, para eliminar características ruidosas.

En el ejemplo siguiente, el uso de un reducido umbral de contracción aumenta la precisión del modelo de 0,81 a 0,82.

nearest_centroid_1 nearest_centroid_2

Ejemplos:

1.6.6. Transformador de vecinos más cercanos

Muchos estimadores de scikit-learn se basan en los vecinos más cercanos: Varios clasificadores y regresores como KNeighborsClassifier y KNeighborsRegressor, pero también algunos métodos de agrupamiento como DBSCAN y SpectralClustering, y algunos incrustados como TSNE y Isomap.

Todos estos estimadores pueden calcular internamente los vecinos más cercanos, pero la mayoría de ellos también aceptan el grafo disperso de los vecinos más cercanos precalculados, como se da en kneighbors_graph y radius_neighbors_graph. Con el modo mode='connectivity', estas funciones devuelven un gráfico binario de adyacencia disperso como se requiere, por ejemplo, en SpectralClustering. Mientras que con mode='distance', devuelven un grafo disperso de distancia como se requiere, por ejemplo, en DBSCAN. Para incluir estas funciones en un pipeline de scikit-learn, también se pueden utilizar las clases correspondientes KNeighborsTransformer y RadiusNeighborsTransformer. Los beneficios de esta API de gráficos dispersos son múltiples.

En primer lugar, el gráfico precalculado puede reutilizarse varias veces, por ejemplo, al variar un parámetro del estimador. Esto se puede hacer manualmente por el usuario, o utilizando las propiedades de almacenamiento en caché de la pipeline de scikit-learn:

>>> from sklearn.manifold import Isomap
>>> from sklearn.neighbors import KNeighborsTransformer
>>> from sklearn.pipeline import make_pipeline
>>> estimator = make_pipeline(
...     KNeighborsTransformer(n_neighbors=5, mode='distance'),
...     Isomap(neighbors_algorithm='precomputed'),
...     memory='/path/to/cache')

En segundo lugar, precalcular el gráfico puede dar un control más fino sobre la estimación de los vecinos más cercanos, por ejemplo, permitiendo el multiprocesamiento a través del parámetro n_jobs, que podría no estar disponible en todos los estimadores.

Finalmente, el precálculo puede ser realizado por estimadores personalizados para utilizar diferentes implementaciones, como los métodos de vecinos más cercanos aproximados, o la implementación con tipos de datos especiales. El grafo disperso de vecinos precalculados debe tener el mismo formato que la salida de radius_neighbors_graph:

  • una matriz CSR (aunque se aceptarán COO, CSC o LIL).

  • sólo almacena explícitamente los vecindarios más cercanos de cada muestra con respecto a los datos de entrenamiento. Esto debería incluir los que se encuentran a una distancia de 0 de un punto de consulta, incluyendo la diagonal de la matriz cuando se calculan los vecindarios más cercanos entre los datos de entrenamiento y ellos mismos.

  • los datos de cada fila deben almacenar la distancia en orden creciente (opcional. Los datos no ordenados serán ordenados de forma estable, lo que añade una sobrecarga computacional).

  • todos los valores en los datos no deben ser negativos.

  • no debe haber indices duplicados en ninguna fila (consulta https://github.com/scipy/scipy/issues/5807).

  • si el algoritmo al que se le pasa la matriz precalculada utiliza k vecinos más cercanos (en lugar del vecindario de radio), se deben almacenar al menos k vecinos en cada fila (o k+1, como se explica en la siguiente nota).

Nota

Cuando se consulta un número específico de vecinos (utilizando KNeighborsTransformer), la definición de n_neighbors es ambigua ya que puede incluir cada punto de entrenamiento como su propio vecino, o excluirlos. Ninguna de las dos opciones es perfecta, ya que incluirlos conduce a un número diferente de vecinos no propios durante el entrenamiento y la prueba, mientras que excluirlos conduce a una diferencia entre fit(X).transform(X) y fit_transform(X), lo que va en contra de la API de scikit-learn. En KNeighborsTransformer utilizamos la definición que incluye cada punto de entrenamiento como su propio vecino en la cuenta de n_neighbors. Sin embargo, por razones de compatibilidad con otros estimadores que utilizan la otra definición, se calculará un vecino extra cuando mode == 'distance'. Para maximizar la compatibilidad con todos los estimadores, una opción segura es incluir siempre un vecino extra en un estimador personalizado de vecinos más cercanos, ya que los vecinos innecesarios serán filtrados por los siguientes estimadores.

Ejemplos:

1.6.7. Análisis de componentes del vecindario

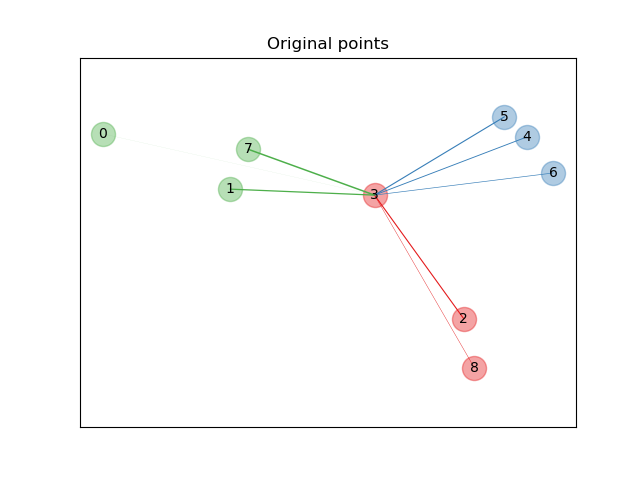
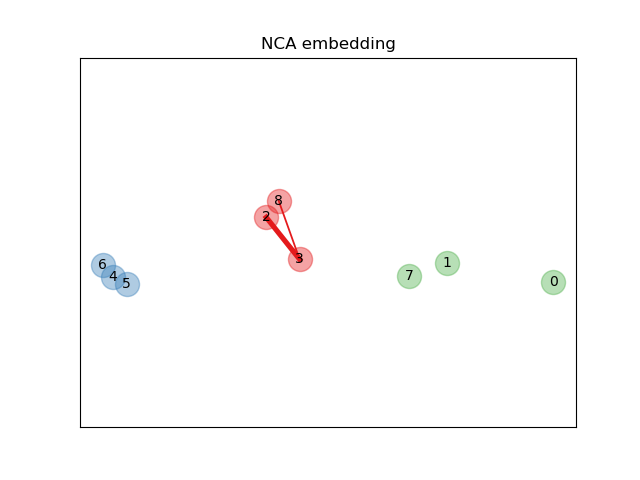
El Análisis de componentes del vecindario (NCA, NeighborhoodComponentsAnalysis) es un algoritmo de aprendizaje de la métrica de la distancia cuyo objetivo es mejorar la exactitud de la clasificación de los vecinos más cercanos en comparación con la distancia euclidiana estándar. El algoritmo maximiza directamente una variante estocástica de la puntuación de los vecinos más cercanos (KNN) en el conjunto de entrenamiento. También puede aprender una proyección lineal de baja dimensión de los datos que puede utilizarse para la visualización de datos y la clasificación rápida.

nca_illustration_1 nca_illustration_2

En la figura ilustrada arriba, consideramos algunos puntos de un conjunto de datos generados aleatoriamente. Nos centramos en la clasificación KNN estocástica del punto nº 3. El grosor de un enlace entre la muestra 3 y otro punto es proporcional a su distancia, y puede verse como el peso relativo (o probabilidad) que una regla de predicción estocástica del vecino más cercano asignaría a este punto. En el espacio original, la muestra 3 tiene muchos vecinos estocásticos de varias clases, por lo que la clase correcta no es muy probable. Sin embargo, en el espacio proyectado aprendido por NCA, los únicos vecinos estocásticos con peso no despreciable son de la misma clase que la muestra 3, lo que garantiza que esta última estará bien clasificada. Consulta la formulación matemática para obtener más detalles.

1.6.7.1. Clasificación

Combinado con un clasificador de vecinos más cercanos (KNeighborsClassifier), el NCA es atractivo para la clasificación porque puede manejar naturalmente problemas de multiclases sin ningún aumento en el tamaño del modelo, y no introduce parámetros adicionales que requieran un ajuste fino por parte del usuario.

Se ha demostrado que la clasificación NCA funciona bien en la práctica para conjuntos de datos de tamaño y dificultad variables. A diferencia de otros métodos relacionados, como el análisis discriminante lineal, el NCA no hace ninguna suposición sobre las distribuciones de las clases. La clasificación del vecino más cercano puede producir naturalmente límites de decisión muy irregulares.

Para utilizar este modelo para la clasificación, es necesario combinar una instancia NeighborhoodComponentsAnalysis que aprende la transformación óptima con una instancia KNeighborsClassifier que realiza la clasificación en el espacio proyectado. Este es un ejemplo que utiliza las dos clases:

>>> from sklearn.neighbors import (NeighborhoodComponentsAnalysis,
... KNeighborsClassifier)
>>> from sklearn.datasets import load_iris
>>> from sklearn.model_selection import train_test_split
>>> from sklearn.pipeline import Pipeline
>>> X, y = load_iris(return_X_y=True)
>>> X_train, X_test, y_train, y_test = train_test_split(X, y,
... stratify=y, test_size=0.7, random_state=42)
>>> nca = NeighborhoodComponentsAnalysis(random_state=42)
>>> knn = KNeighborsClassifier(n_neighbors=3)
>>> nca_pipe = Pipeline([('nca', nca), ('knn', knn)])
>>> nca_pipe.fit(X_train, y_train)
Pipeline(...)
>>> print(nca_pipe.score(X_test, y_test))
0.96190476...

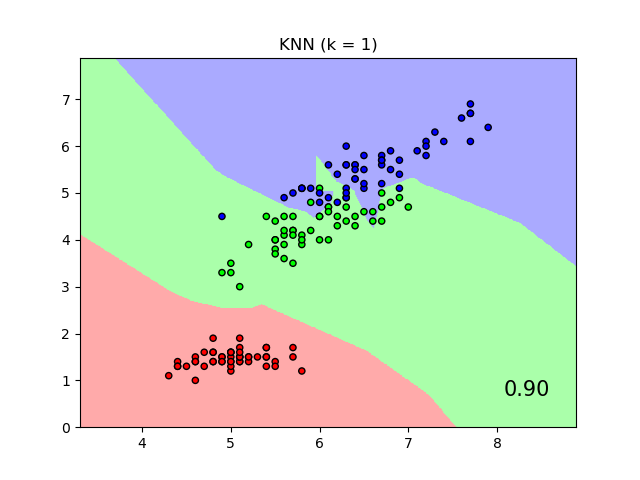
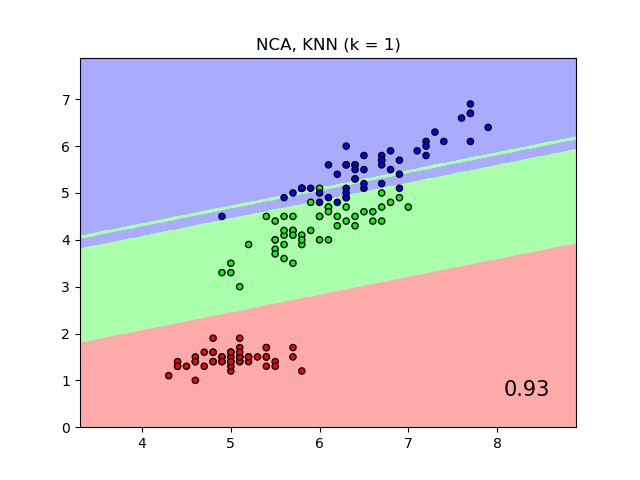
nca_classification_1 nca_classification_2

El gráfico muestra los límites de decisión para la clasificación de vecino más cercano y la clasificación de análisis de componentes del vecindario en el conjunto de datos iris, cuando se entrena y puntúa sólo con dos características, a efectos de visualización.

1.6.7.2. Reducción de Dimensionalidad

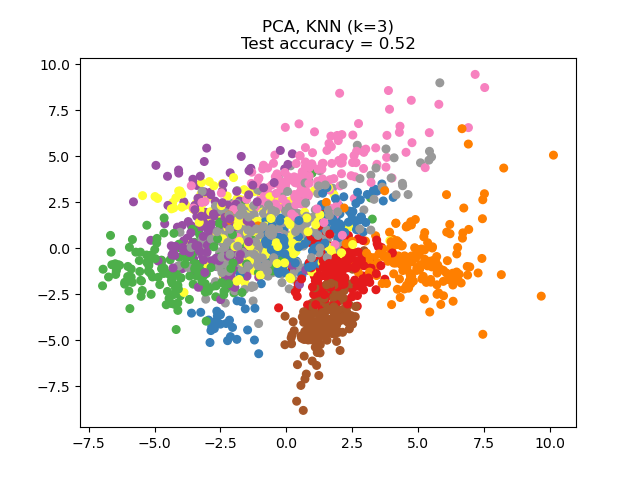
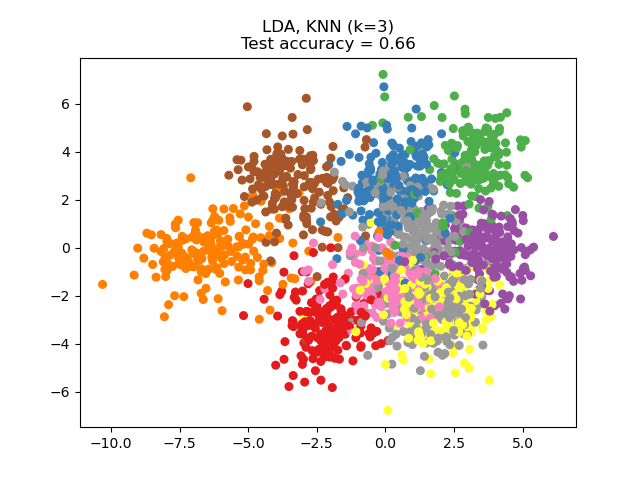
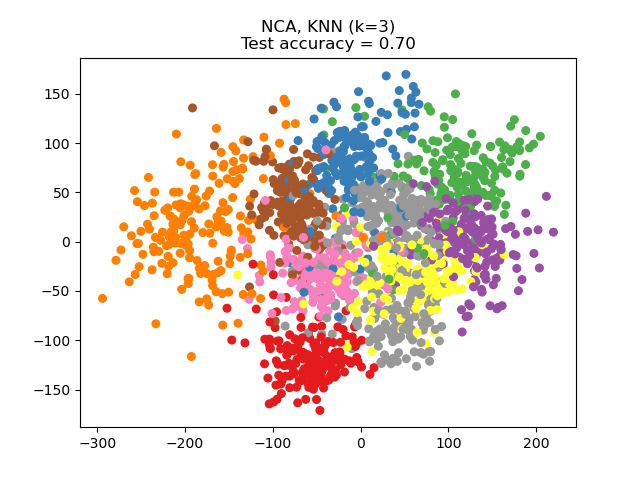
El NCA puede utilizarse para realizar una reducción de la dimensionalidad supervisada. Los datos de entrada se proyectan en un subespacio lineal formado por las direcciones que minimizan el objetivo del NCA. La dimensionalidad deseada puede establecerse mediante el parámetro n_components. Por ejemplo, la siguiente figura muestra una comparación de la reducción de la dimensionalidad con el Análisis de Componentes Principales (PCA), el Análisis Discriminante Lineal ( LinearDiscriminantAnalysis) y el Análisis de Componentes del Vecindario (NeighborhoodComponentsAnalysis) en el conjunto de datos Digits, un conjunto de datos con tamaño \(n_{samples} = 1797\) y \(n_{features} = 64\). El conjunto de datos se divide en un conjunto de entrenamiento y otro de prueba de igual tamaño, y luego se estandariza. Para la evaluación, se calcula la exactitud de la clasificación de 3 vecinos más cercanos en los puntos proyectados bidimensionales encontrados por cada método. Cada muestra de datos pertenece a una de las 10 clases.

nca_dim_reduction_1 nca_dim_reduction_2 nca_dim_reduction_3

Ejemplos:

1.6.7.3. Formulación matemática

El objetivo del NCA es aprender una matriz de transformación lineal óptima de tamaño (n_components, n_features), que maximice la suma sobre todas las muestras \(i\) de la probabilidad \(p_i\) de que \(i\) se clasifique correctamente, es decir:

\[\underset{L}{\arg\max} \sum\limits_{i=0}^{N - 1} p_{i}\]

con \(N\) = n_samples y \(p_i\) la probabilidad de que la muestra \(i\) se clasifique correctamente según una regla estocástica de vecinos más cercanos en el espacio incrustado aprendido:

\[p_{i}=\sum\limits_{j \in C_i}{p_{i j}}\]

donde \(C_i\) es el conjunto de puntos en la misma clase que la muestra \(i\), y \(p_{i j}\) es el máximo softmax sobre distancias euclidianas en el espacio incrustado:

\[p_{i j} = \frac{\exp(-||L x_i - L x_j||^2)}{\sum\limits_{k \ne i} {\exp{-(||L x_i - L x_k||^2)}}} , \quad p_{i i} = 0\]

1.6.7.3.1. Distancia de Mahalanobis

El NCA puede verse como el aprendizaje de una métrica de distancia de Mahalanobis (al cuadrado):

\[|| L(x_i - x_j)||^2 = (x_i - x_j)^TM(x_i - x_j),\]

donde \(M = L^T L\) es una matriz simétrica semidefinida positiva de tamaño (n_features, n_features).

1.6.7.4. Implementación

Esta implementación sigue lo explicado en el artículo original 1. Para el método de optimización, actualmente utiliza el L-BFGS-B de scipy con un cálculo de gradiente completo en cada iteración, para evitar afinar la tasa de aprendizaje y proporcionar un aprendizaje estable.

Puedes ver los ejemplos a continuación y la cadena de documentación de NeighborhoodComponentsAnalysis.fit para más información.

1.6.7.5. Complejidad

1.6.7.5.1. Formación

El NCA almacena una matriz de distancias entre pares, ocupando n_samples ** 2 de memoria. La complejidad del tiempo depende del número de iteraciones realizadas por el algoritmo de optimización. Sin embargo, se puede establecer el número máximo de iteraciones con el argumento max_iter. Para cada iteración, la complejidad temporal es O(n_components x n_samples x min(n_samples, n_features)).

1.6.7.5.2. Transformación

Aquí la operación transform devuelve \(LX^T\), por lo tanto su complejidad de tiempo es igual a n_components * n_features * n_samples_test. No hay complejidad de espacio añadida en la operación.

Referencias:

1

«Neighbourhood Components Analysis», J. Goldberger, S. Roweis, G. Hinton, R. Salakhutdinov, Advances in Neural Information Processing Systems, Vol. 17, mayo 2005, pp. 513-520.

Entrada de Wikipedia en Análisis de Componentes del Vecindario