Ilustración del Análisis de los Componentes del Vecindario (Neighborhood Components Analysis)

Este ejemplo ilustra una métrica de distancia aprendida que maximiza la exactitud de la clasificación de los vecinos más cercanos. Proporciona una representación visual de esta métrica en comparación con el espacio de puntos original. Consulta el manual de usuario para obtener más información.

# License: BSD 3 clause

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.neighbors import NeighborhoodComponentsAnalysis
from matplotlib import cm
from scipy.special import logsumexp

print(__doc__)

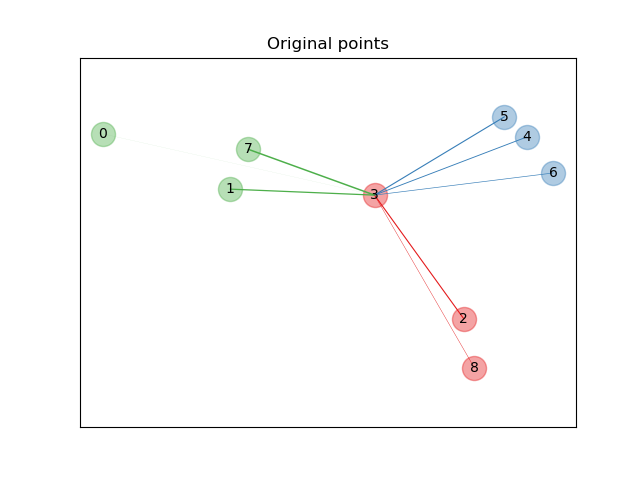
Puntos originales

Primero creamos un conjunto de datos de 9 muestras de 3 clases, y trazamos los puntos en el espacio original. Para este ejemplo, nos centramos en la clasificación del punto n.º 3. El grosor de un enlace entre el punto n.º 3 y otro punto es proporcional a su distancia.

X, y = make_classification(n_samples=9, n_features=2, n_informative=2,
                           n_redundant=0, n_classes=3, n_clusters_per_class=1,
                           class_sep=1.0, random_state=0)

plt.figure(1)
ax = plt.gca()
for i in range(X.shape[0]):
    ax.text(X[i, 0], X[i, 1], str(i), va='center', ha='center')
    ax.scatter(X[i, 0], X[i, 1], s=300, c=cm.Set1(y[[i]]), alpha=0.4)

ax.set_title("Original points")
ax.axes.get_xaxis().set_visible(False)
ax.axes.get_yaxis().set_visible(False)
ax.axis('equal')  # so that boundaries are displayed correctly as circles


def link_thickness_i(X, i):
    diff_embedded = X[i] - X
    dist_embedded = np.einsum('ij,ij->i', diff_embedded,
                              diff_embedded)
    dist_embedded[i] = np.inf

    # compute exponentiated distances (use the log-sum-exp trick to
    # avoid numerical instabilities
    exp_dist_embedded = np.exp(-dist_embedded -
                               logsumexp(-dist_embedded))
    return exp_dist_embedded


def relate_point(X, i, ax):
    pt_i = X[i]
    for j, pt_j in enumerate(X):
        thickness = link_thickness_i(X, i)
        if i != j:
            line = ([pt_i[0], pt_j[0]], [pt_i[1], pt_j[1]])
            ax.plot(*line, c=cm.Set1(y[j]),
                    linewidth=5*thickness[j])


i = 3
relate_point(X, i, ax)
plt.show()

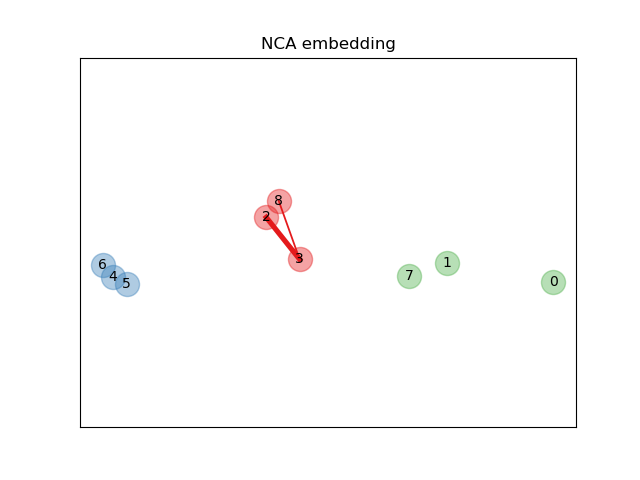
Aprender una incrustación (embedding)

Utilizamos NeighborhoodComponentsAnalysis para aprender una incrustación (embedding) y graficar los puntos después de la transformación. A continuación, tomamos la incrustación y encontramos los vecinos más cercanos.

nca = NeighborhoodComponentsAnalysis(max_iter=30, random_state=0)
nca = nca.fit(X, y)

plt.figure(2)
ax2 = plt.gca()
X_embedded = nca.transform(X)
relate_point(X_embedded, i, ax2)

for i in range(len(X)):
    ax2.text(X_embedded[i, 0], X_embedded[i, 1], str(i),
             va='center', ha='center')
    ax2.scatter(X_embedded[i, 0], X_embedded[i, 1], s=300, c=cm.Set1(y[[i]]),
                alpha=0.4)

ax2.set_title("NCA embedding")
ax2.axes.get_xaxis().set_visible(False)
ax2.axes.get_yaxis().set_visible(False)
ax2.axis('equal')
plt.show()