1.7. Procesos Gaussianos

Los procesos Gaussianos (GP) son un método genérico de aprendizaje supervisado diseñado para resolver problemas de regresión y clasificación probabilística.

Las ventajas de los procesos Gaussianos son:

• La predicción interpola las observaciones (al menos para los núcleos regulares).

• La predicción es probabilística (gaussiana), por lo que se pueden calcular intervalos de confianza empíricos y decidir, en base a ellos, si se debe reajustar (ajuste en línea, ajuste adaptativo) la predicción en alguna región de interés.

• Versátil: se pueden especificar diferentes núcleos. Se proporcionan núcleos comunes, pero también es posible especificar núcleos personalizados.

Las desventajas de los procesos Gaussianos incluyen:

• No son dispersos, es decir, utilizan toda la información de las muestras para realizar la predicción.

• Pierden eficacia en espacios de alta dimensión, es decir, cuando el número de características supera algunas decenas.

1.7.1. Regresión de Procesos Gaussianos (GPR)

El GaussianProcessRegressor implementa procesos Gaussianos (GP) con fines de regresión. Para ello, es necesario especificar la distribución a priori del GP. La media a priori se supone constante y cero (para normalize_y=False) o la media de los datos de entrenamiento (para normalize_y=True). La covarianza a priori se especifica pasando un objeto kernel. Los hiperparámetros del núcleo se optimizan durante el ajuste de GaussianProcessRegressor maximizando la verosimilitud marginal logarítmica (log-marginal-likelihood, o LML) basado en el optimizer que se le pasa. Como el LML puede tener múltiples óptimos locales, el optimizador puede iniciarse repetidamente especificando n_restarts_optimizer. La primera ejecución se realiza siempre a partir de los valores iniciales de los hiperparámetros del núcleo; las ejecuciones posteriores se realizan a partir de los valores de los hiperparámetros que se han elegido aleatoriamente del rango de valores permitidos. Si los hiperparámetros iniciales deben mantenerse fijos, se puede pasar None como optimizador.

El nivel de ruido en los objetivos puede especificarse pasándolo a través del parámetro alpha, ya sea globalmente como escalar o por punto de datos. Ten en cuenta que un nivel de ruido moderado también puede ser útil para tratar los problemas numéricos durante el ajuste, ya que se implementa efectivamente como regularización de Tikhonov, es decir, añadiéndolo a la diagonal de la matriz del núcleo. Una alternativa para la especificación explícita del nivel de ruido es incluir un componente WhiteKernel en el núcleo, que puede estimar el nivel de ruido global a partir de los datos (véase el ejemplo siguiente).

La implementación se basa en el algoritmo 2.1 de [RW2006]. Además de la API de los estimadores estándar de scikit-learn, GaussianProcessRegressor:

• permite la predicción sin ajuste previo (basado en el previo GP)

• proporciona un método adicional sample_y(X), que evalúa las muestras extraídas del GPR (a priori o a posteriori) en entradas específicas

• expone un método log_marginal_likelihood(theta), que puede ser usado externamente para otras maneras de seleccionar hiperparámetros, por ejemplo, a través de la cadena de Markov Monte Carlo.

1.7.2. Ejemplos de GPR

1.7.2.1. GPR con estimación de nivel de ruido

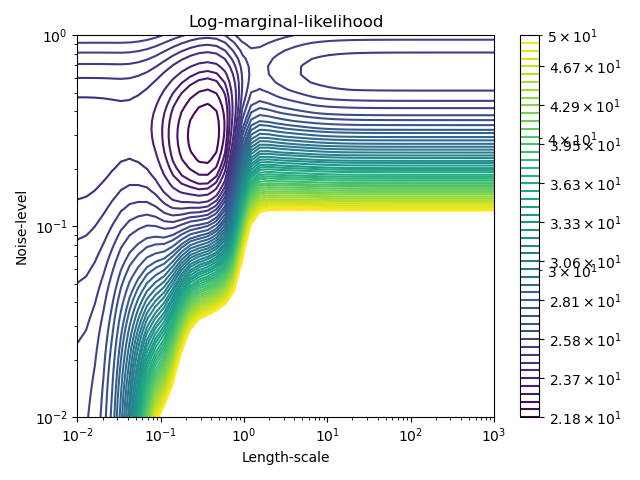
Este ejemplo ilustra que la GPR con un núcleo de suma que incluye un WhiteKernel puede estimar el nivel de ruido de los datos. Una descripción de la verosimilitud marginal logarítmica (LML) muestra que existen dos máximos locales de LML.

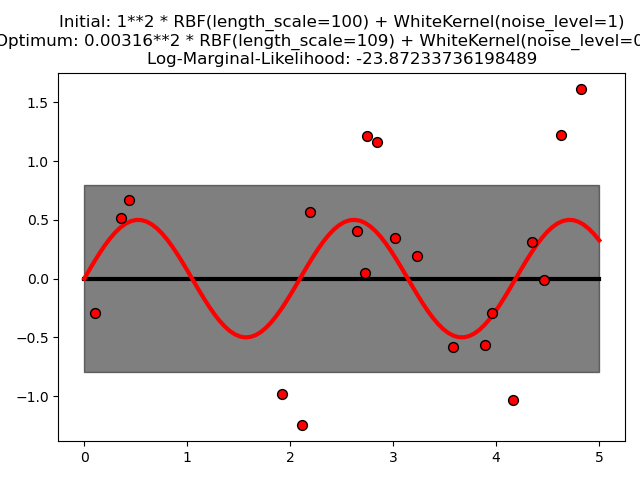
El primero corresponde a un modelo con un alto nivel de ruido y una gran escala de longitud, que explica todas las variaciones de los datos debidas al ruido.

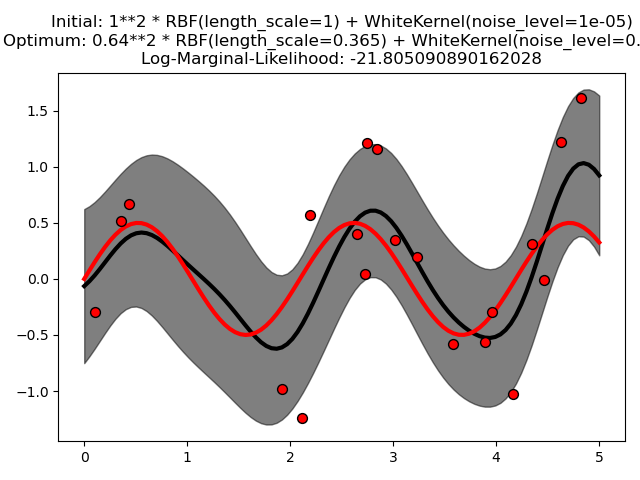
El segundo tiene un nivel de ruido menor y una escala de longitud más corta, lo que explica la mayor parte de la variación por la relación funcional sin ruido. El segundo modelo tiene una mayor verosimilitud; sin embargo, dependiendo del valor inicial de los hiperparámetros, la optimización basada en el gradiente también podría converger a la solución de alto ruido. Por lo tanto, es importante repetir la optimización varias veces para diferentes inicializaciones.

1.7.2.2. Comparación de la GPR y la regresión de kernel de Ridge

Tanto la regresión cresta de núcleo (cuyas siglas en inglés son KRR) como la GPR aprenden una función objetivo empleando internamente el «truco del núcleo». KRR aprende una función lineal en el espacio inducido por el núcleo respectivo que corresponde a una función no lineal en el espacio original. La función lineal en el espacio del núcleo se elige en función de la pérdida de error cuadrático medio con regularización de cresta. La GPR utiliza el núcleo para definir la covarianza de una distribución a priori sobre las funciones objetivo y utiliza los datos de entrenamiento observados para definir una función de verosimilitud. Basándose en el teorema de Bayes, se define una distribución posterior (gaussiana) sobre las funciones objetivo, cuya media se utiliza para la predicción.

Una de las principales diferencias es que GPR puede elegir los hiperparámetros del núcleo basándose en el gradiente de ascenso de la función de verosimilitud marginal, mientras que KRR tiene que realizar una búsqueda en cuadrícula en una función de pérdida validada de forma cruzada (pérdida de error cuadrático medio). Otra distinción es que GPR aprende un modelo generativo y probabilístico de la función objetivo y, por tanto, puede proporcionar intervalos de confianza significativos y muestras posteriores junto con las predicciones, mientras que KRR sólo proporciona predicciones.

La siguiente figura ilustra ambos métodos en un conjunto de datos artificial, que consiste en una función objetivo sinusoidal y un fuerte ruido. La figura compara el modelo aprendido de KRR y GPR basado en un núcleo ExpSineSquared, que es adecuado para el aprendizaje de funciones periódicas. Los hiperparámetros del núcleo controlan la suavidad (length_scale) y la periodicidad del núcleo (periodicity). Además, el nivel de ruido de los datos es aprendido explícitamente por GPR mediante un componente adicional WhiteKernel en el núcleo y por el parámetro de regularización alfa de KRR.

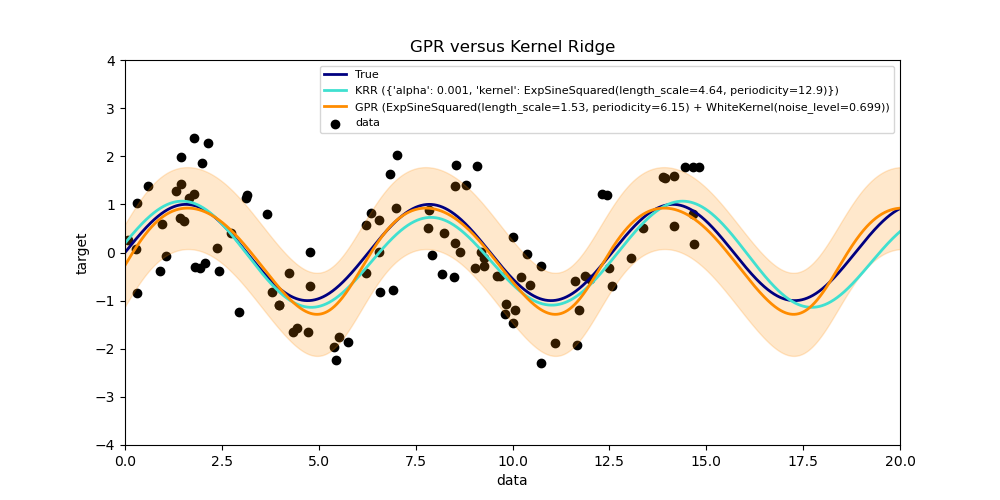
La figura muestra que ambos métodos aprenden modelos razonables de la función objetivo. GPR identifica correctamente que la periodicidad de la función es aproximadamente \(2*\pi\) (6.28), mientras que KRR elige la periodicidad duplicada \(4*\pi\) . Además, GPR proporciona límites de confianza razonables en la predicción que no están disponibles para KRR. Una diferencia importante entre los dos métodos es el tiempo necesario para el ajuste y la predicción: mientras que el ajuste de KRR es rápido en principio, la búsqueda en cuadrícula para la optimización de los hiperparámetros escala exponencialmente con el número de hiperparámetros («maldición de la dimensionalidad»). La optimización de los parámetros basada en el gradiente en GPR no sufre este escalamiento exponencial y, por tanto, es considerablemente más rápida en este ejemplo con un espacio de hiperparámetros tridimensional. El tiempo de predicción es similar; sin embargo, generar la varianza de la distribución de predicción de GPR lleva bastante más tiempo que sólo predecir la media.

1.7.2.3. GPR en datos de CO2 de Mauna Loa

Este ejemplo se basa en la Sección 5.4.3 de [RW2006]. Ilustra un ejemplo de ingeniería de núcleos complejos y optimización de hiperparámetros utilizando el ascenso de gradiente en la verosimilitud marginal logarítmica. Los datos consisten en las concentraciones medias mensuales de CO2 atmosférico (en partes por millón en volumen (ppmv)) recogidas en el Observatorio de Mauna Loa en Hawai, entre 1958 y 1997. El objetivo es modelar la concentración de CO2 como función del tiempo t.

El núcleo se compone de varios términos que son responsables de explicar diferentes propiedades de la señal:

• una tendencia suave y ascendente a largo plazo debe ser explicada por un núcleo RBF. El núcleo RBF con una gran escala de longitud obliga a que este componente sea suavizado; no se exige que la tendencia sea ascendente, lo que deja esta elección a la GP. La escala de longitud específica y la amplitud son hiperparámetros libres.

• un componente estacional, que debe ser explicado por el núcleo periódico ExpSineSquared con una periodicidad fija de 1 año. La escala de longitud de este componente periódico, que controla su suavizado (smoothness), es un parámetro libre. Para permitir el decaimiento de la periodicidad exacta, se toma el producto con un núcleo RBF. La escala de longitud de este componente RBF controla el tiempo de deterioro y es otro parámetro libre.

• las irregularidades a corto y a mediano plazo deben explicarse mediante un componente del núcleo RationalQuadratic, cuya escala de longitud y parámetro alfa, que determina la difusividad de las escalas de longitud, deben determinarse. Según [RW2006], estas irregularidades se pueden explicar mejor con un componente de núcleo RationalQuadratic que con uno RBF, probablemente porque puede acomodar varias escalas de longitud.

• un término de «ruido», que consiste en una contribución del núcleo RBF, que explicará los componentes de ruido correlacionados, como los fenómenos meteorológicos locales, y una contribución del WhiteKernel para el ruido blanco. Las amplitudes relativas y la escala de longitud del RBF son otros parámetros libres.

Al maximizar la verosimilitud marginal logarítmica después de restar la media del objetivo, se obtiene el siguiente núcleo con un LML de -83,214:

34.4**2 * RBF(length_scale=41.8)
+ 3.27**2 * RBF(length_scale=180) * ExpSineSquared(length_scale=1.44,
                                                   periodicity=1)
+ 0.446**2 * RationalQuadratic(alpha=17.7, length_scale=0.957)
+ 0.197**2 * RBF(length_scale=0.138) + WhiteKernel(noise_level=0.0336)

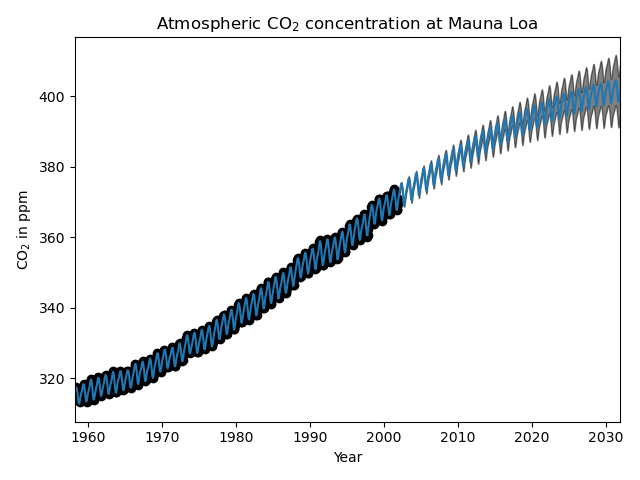
Así, la mayor parte de la señal objetivo (34,4 partes por millón) se explica por una tendencia ascendente a largo plazo (escala de longitud de 41,8 años). El componente periódico tiene una amplitud de 3,27 ppm, un tiempo de decaimiento de 180 años y una escala de longitud de 1,44. El largo tiempo de deterioro indica que tenemos una componente estacional localmente muy cercana a la periódica. El ruido correlacionado tiene una amplitud de 0,197ppm con una escala de longitud de 0,138 años y una contribución de ruido blanco de 0,197 ppm. Por tanto, el nivel de ruido global es muy pequeño, lo que indica que los datos pueden ser explicados muy bien por el modelo. La figura muestra también que el modelo hace predicciones muy seguras hasta el año 2015 aproximadamente

1.7.3. Clasificación de Procesos Gaussianos (GPC)

El GaussianProcessClassifier implementa procesos Gaussianos (GP en inglés) con fines de clasificación, más específicamente para la clasificación probabilística, donde las predicciones de prueba toman la forma de probabilidades de clase. GaussianProcessClassifier coloca un GP previo en una función latente \(f\), que luego se comprime a través de una función de enlace para obtener la clasificación probabilística. La función latente \(f\) es una función denominada incómoda (nuisance function), cuyos valores no se observan y no son relevantes por sí mismos. Su propósito es permitir una formulación conveniente del modelo, y \(f\) se elimina (se integra) durante la predicción. GaussianProcessClassifier implementa la función de enlace logístico, para la cual la integral no puede ser calculada analíticamente pero es fácilmente aproximada en el caso binario.

En contraste con la situación de la regresión, la posterior de la función latente \(f\) no es gaussiana incluso para un GP previo, ya que una verosimilitud gaussiana es inapropiada para las etiquetas de clase discretas. En su lugar, se utiliza una probabilidad no gaussiana correspondiente a la función de enlace logístico (logit). GaussianProcessClassifier aproxima la posterior no gaussiana con una gaussiana basada en la aproximación de Laplace. Se pueden encontrar más detalles en el capítulo 3 de [RW2006].

Se asume que la media a priori del GP es cero. La covarianza a priori se especifica pasando un objeto kernel. Los hiperparámetros del kernel se optimizan durante el ajuste de GaussianProcessRegressor maximizando la verosimilitud marginal logarítmica (LML) basado en el optimizer que se le pasa. Como el LML puede tener múltiples óptimos locales, el optimizador puede iniciarse repetidamente especificando n_restarts_optimizer. La primera ejecución se realiza siempre a partir de los valores iniciales de los hiperparámetros del kernel; las ejecuciones posteriores se realizan a partir de los valores de los hiperparámetros que se han elegido aleatoriamente del rango de valores permitidos. Si los hiperparámetros iniciales deben mantenerse fijos, se puede pasar None como optimizador.

GaussianProcessClassifier admite la clasificación multiclase mediante el entrenamiento y la predicción basados en uno-contra-el-resto o uno-contra-uno. En uno-contra-resto, se ajusta un clasificador de proceso gaussiano binario para cada clase, que se entrena para separar esta clase del resto. En «one_vs_one», se ajusta un clasificador de proceso gaussiano binario para cada par de clases, que se entrena para separar estas dos clases. Las predicciones de estos predictores binarios se combinan en predicciones multiclase. Consulte la sección de clasificación multiclase para obtener más detalles.

En el caso de la clasificación del proceso gaussiano, «one_vs_one» podría ser computacionalmente más económico, ya que tiene que resolver muchos problemas que implican sólo un subconjunto del conjunto de entrenamiento, en lugar de menos problemas en todo el conjunto de datos. Dado que la clasificación del proceso gaussiano se escala cúbicamente con el tamaño del conjunto de datos, esto podría ser considerablemente más rápido. Sin embargo, ten en cuenta que «one_vs_one» no admite la predicción de estimaciones de probabilidad, sino sólo predicciones directas. Además, ten en cuenta que GaussianProcessClassifier no implementa (todavía) una verdadera aproximación de Laplace multiclase internamente, sino que, como se ha comentado anteriormente, se basa en la resolución de varias tareas de clasificación binaria internamente, que se combinan utilizando uno-versus-el-resto o uno-versus-uno.

1.7.4. Ejemplos de GPC

1.7.4.1. Predicciones probabilísticas con GPC

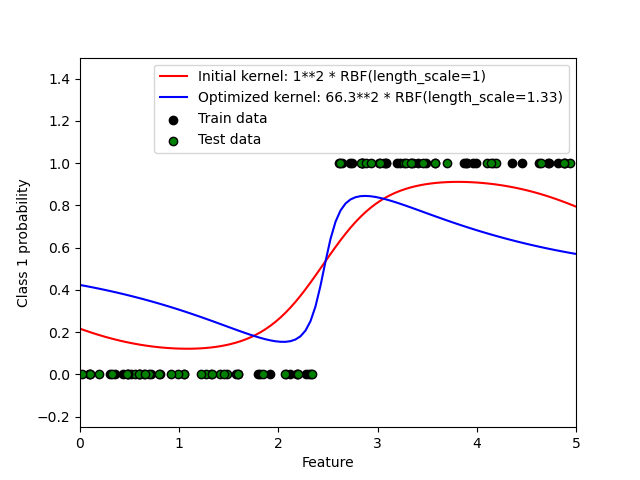
Este ejemplo ilustra la probabilidad pronosticada de GPC para un núcleo RBF con diferentes elecciones de los hiperparámetros. La primera figura muestra la probabilidad predicha de GPC con hiperparámetros elegidos arbitrariamente y con los hiperparámetros correspondientes a la máxima verosimilitud marginal logarítmica (LML).

Aunque los hiperparámetros elegidos mediante la optimización de LML tienen un LML considerablemente mayor, su rendimiento es ligeramente inferior de acuerdo con la pérdida logarítmica en los datos de prueba. La figura muestra que esto se debe a que exhiben un cambio pronunciado de las probabilidades de clase en los límites de la clase (lo cual es bueno) pero tienen probabilidades predichas cercanas a 0,5 lejos de los límites de la clase (lo cual es malo) Este efecto indeseable es causado por la aproximación de Laplace utilizada internamente por GPC.

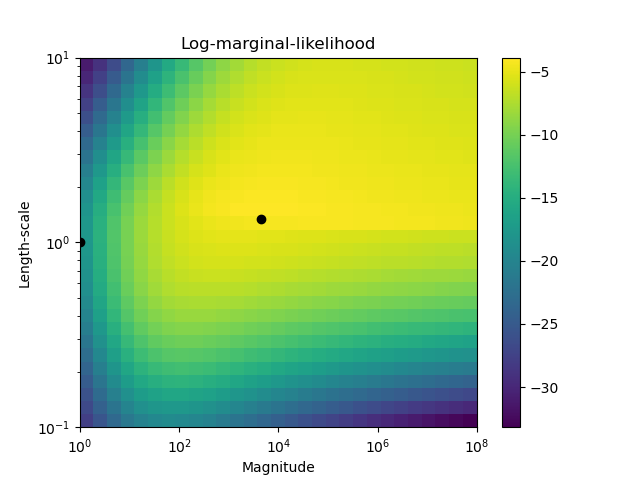
La segunda figura muestra la verosimilitud marginal logarítmica para diferentes opciones de los hiperparámetros del núcleo, destacando las dos opciones de los hiperparámetros utilizados en la primera figura mediante puntos negros.

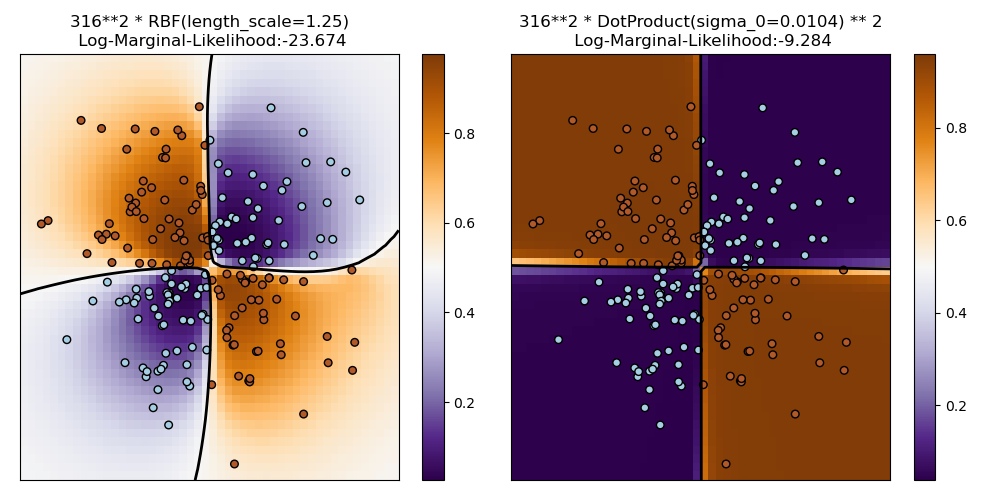
1.7.4.2. Ejemplo de GPC en el conjunto de datos XOR

Este ejemplo ilustra la GPC en datos XOR. Se comparan un núcleo estacionario e isotrópico (RBF) y un núcleo no estacionario (DotProduct). En este conjunto de datos concreto, el núcleo DotProduct obtiene resultados considerablemente mejores porque los límites de la clase son lineales y coinciden con los ejes de coordenadas. En la práctica, sin embargo, los núcleos estacionarios como RBF suelen obtener mejores resultados.

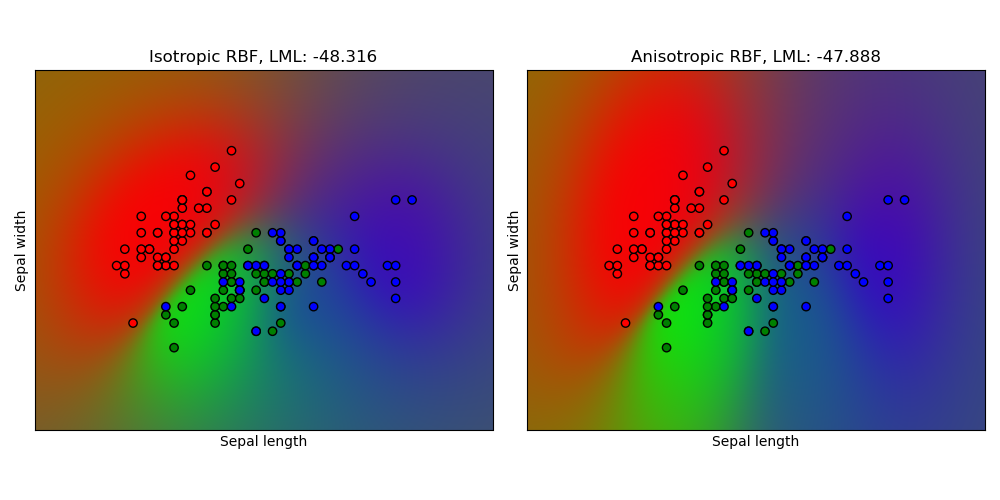
1.7.4.3. Clasificación de procesos gaussianos (GPC) en el conjunto de datos iris

Este ejemplo muestra la probabilidad predicha de GPC para un núcleo RBF isotrópico y anisotrópico en una versión bidimensional para el conjunto de datos del iris. Esto muestra la aplicabilidad de la GPC a la clasificación no binaria. El núcleo RBF anisotrópico obtiene una verosimilitud marginal logarítmica (log-marginal-likelihood) ligeramente superior al asignar diferentes escalas de longitud a las dos dimensiones de características.

1.7.5. Núcleos para procesos gaussianos

Los kernels (también llamados «funciones de covarianza» en el contexto de los GP) son un ingrediente crucial de los GP que determinan la forma de la distribución a priori (prior) y a posteriori (posterior) del GP. Codifican las suposiciones sobre la función que se aprende definiendo la «similitud» de dos puntos de datos combinada con la suposición de que los puntos de datos similares deberían tener valores objetivo similares. Se pueden distinguir dos categorías de kernels: los kernels estacionarios dependen sólo de la distancia de dos puntos de datos y no de sus valores absolutos \(k(x_i, x_j)= k(d(x_i, x_j))\) y, por tanto, son invariables a las traslaciones en el espacio de entrada, mientras que los kernels no estacionarios dependen también de los valores específicos de los puntos de datos. Los kernels estacionarios pueden subdividirse en kernels isotrópicos y anisotrópicos, donde los kernels isotrópicos también son invariantes a las rotaciones en el espacio de entrada. Para más detalles, nos remitimos al capítulo 4 de [RW2006]. Para obtener orientación sobre la mejor manera de combinar diferentes kernels, nos remitimos a [Duv2014].

1.7.5.1. API del núcleo de proceso gaussiano

El uso principal de un Kernel es calcular la covarianza de la GP entre puntos de datos. Para ello, se puede llamar al método __call__ del núcleo. Este método puede utilizarse para calcular la «autocovarianza» de todos los pares de puntos de datos de un arreglo 2D X, o la «covarianza cruzada» de todas las combinaciones de puntos de datos de un arreglo 2D X con puntos de datos de una matriz 2D Y. La siguiente identidad es válida para todos los núcleos k (excepto para el WhiteKernel): k(X) == K(X, Y=X)

Si sólo se utiliza la diagonal de la autocovarianza, se puede llamar al método diag() de un núcleo, que es más eficiente computacionalmente que la llamada equivalente a __call__: np.diag(k(X, X)) == k.diag(X)

Los núcleos están parametrizados por un vector \(\theta\) de hiperparámetros. Estos hiperparámetros pueden, por ejemplo, controlar las escalas de longitud o la periodicidad de un núcleo (véase más adelante). Todos los núcleos soportan el cálculo de gradientes analíticos de la autocovarianza del núcleo con respecto a \(log(\theta)\) mediante la configuración de eval_gradient=True en el método __call__. Es decir, se devuelve una matriz (len(X), len(X), len(theta)) donde la entrada [i, j, l] contiene \(\frac{parcial k_\theta(x_i, x_j)}{\parcial log(\theta_l)}\). Este gradiente es utilizado por el proceso gaussiano (tanto el regresor como el clasificador) en el cálculo del gradiente de la verosimilitud marginal logarítmica (log-marginal-likelihood), que a su vez se utiliza para determinar el valor de \(\theta\), que maximiza el logaritmo de probabilidad marginal, a través del ascenso del gradiente. Para cada hiperparámetro, es necesario especificar el valor inicial y los límites al crear una instancia del núcleo. El valor actual de \(\theta\) puede obtenerse y establecerse mediante la propiedad theta del objeto Kernel. Además, se puede acceder a los límites de los hiperparámetros mediante la propiedad bounds del núcleo. Observa que ambas propiedades (theta y bounds) devuelven valores transformados logarítmicamente de los valores utilizados internamente, ya que suelen ser más susceptibles de una optimización basada en el gradiente. La especificación de cada hiperparámetro se almacena en forma de una instancia de Hyperparameter en el núcleo respectivo. Ten en cuenta que un núcleo que utiliza un hiperparámetro con nombre «x» debe tener los atributos self.x y self.x_bounds.

La clase base abstracta para todos los núcleos es Kernel. El núcleo (kernel) implementa una interfaz similar a la de Estimator, proporcionando los métodos get_params(), set_params(), y clone(). Esto permite establecer los valores del núcleo también a través de metaestimadores como Pipeline o GridSearch. Ten en cuenta que, debido a la estructura anidada de los núcleos (al aplicar operadores del núcleo, como podrás ver más adelante), los nombres de los parámetros del núcleo pueden resultar relativamente complicados. En general, para un operador de núcleo binario, los parámetros del operando izquierdo llevan el prefijo k1__ y los parámetros del operando derecho el prefijo k2__. Un método adicional de utilidad es clone_with_theta(theta), que devuelve una versión clonada del núcleo pero con los hiperparámetros ajustados a theta. Un ejemplo de ello:

>>> from sklearn.gaussian_process.kernels import ConstantKernel, RBF
>>> kernel = ConstantKernel(constant_value=1.0, constant_value_bounds=(0.0, 10.0)) * RBF(length_scale=0.5, length_scale_bounds=(0.0, 10.0)) + RBF(length_scale=2.0, length_scale_bounds=(0.0, 10.0))
>>> for hyperparameter in kernel.hyperparameters: print(hyperparameter)
Hyperparameter(name='k1__k1__constant_value', value_type='numeric', bounds=array([[ 0., 10.]]), n_elements=1, fixed=False)
Hyperparameter(name='k1__k2__length_scale', value_type='numeric', bounds=array([[ 0., 10.]]), n_elements=1, fixed=False)
Hyperparameter(name='k2__length_scale', value_type='numeric', bounds=array([[ 0., 10.]]), n_elements=1, fixed=False)
>>> params = kernel.get_params()
>>> for key in sorted(params): print("%s : %s" % (key, params[key]))
k1 : 1**2 * RBF(length_scale=0.5)
k1__k1 : 1**2
k1__k1__constant_value : 1.0
k1__k1__constant_value_bounds : (0.0, 10.0)
k1__k2 : RBF(length_scale=0.5)
k1__k2__length_scale : 0.5
k1__k2__length_scale_bounds : (0.0, 10.0)
k2 : RBF(length_scale=2)
k2__length_scale : 2.0
k2__length_scale_bounds : (0.0, 10.0)
>>> print(kernel.theta)  # Note: log-transformed
[ 0.         -0.69314718  0.69314718]
>>> print(kernel.bounds)  # Note: log-transformed
[[      -inf 2.30258509]
 [      -inf 2.30258509]
 [      -inf 2.30258509]]

Todos los núcleos de procesos gaussianos son interoperables con sklearn.metrics.pairwise y viceversa: las instancias de las subclases de Kernel pueden pasarse como metric a pairwise_kernels de sklearn.metrics.pairwise. Además, las funciones del núcleo de pares (pairwise) pueden utilizarse como núcleos de GP utilizando la clase envolvente PairwiseKernel. La única advertencia es que el gradiente de los hiperparámetros no es analítico, sino numérico, y todos esos núcleos sólo admiten distancias isotrópicas. El parámetro gamma se considera un hiperparámetro y puede ser optimizado. Los demás parámetros del núcleo se establecen directamente en la inicialización y se mantienen fijos.

1.7.5.2. Núcleos (kernels) básicos

El núcleo ConstantKernel puede utilizarse como parte de un núcleo Product en el que se escala la magnitud del otro factor (núcleo) o como parte de un núcleo Sum, en el que se modifica la media del proceso gaussiano. Depende de un parámetro \(constant\_value\). Se define como:

\[k(x_i, x_j) = constant\_value \;\forall\; x_1, x_2\]

El principal caso de uso del núcleo WhiteKernel es como parte de un núcleo de suma en el que explica el componente de ruido de la señal. El ajuste de su parámetro \(noise\_level\) corresponde a la estimación del nivel de ruido. Se define como:

\[k(x_i, x_j) = noise\_level \text{ if } x_i == x_j \text{ else } 0\]

1.7.5.3. Operadores de núcleo

Los operadores de núcleo toman uno o dos núcleos base y los combinan en un nuevo núcleo. El núcleo Sum toma dos núcleos \(k_1\) y \(k_2\) y los combina mediante \(k_{sum}(X, Y) = k_1(X, Y) + k_2(X, Y)\). El núcleo Product toma dos núcleos \(k_1\) y \(k_2\) y los combina mediante \(k_{product}(X, Y) = k_1(X, Y) * k_2(X, Y)\). El núcleo Exponentiation toma un núcleo base y un parámetro escalar \(p\) y los combina mediante \(k_{exp}(X, Y) = k(X, Y)^p\). Tenga en cuenta que los métodos mágicos __add__, __mul___ y __pow__ se anulan en los objetos Kernel, por lo que se puede utilizar, por ejemplo, RBF() + RBF() como un atajo para Sum(RBF(), RBF()).

1.7.5.4. Núcleo de la Función de Base Radial (RBF)

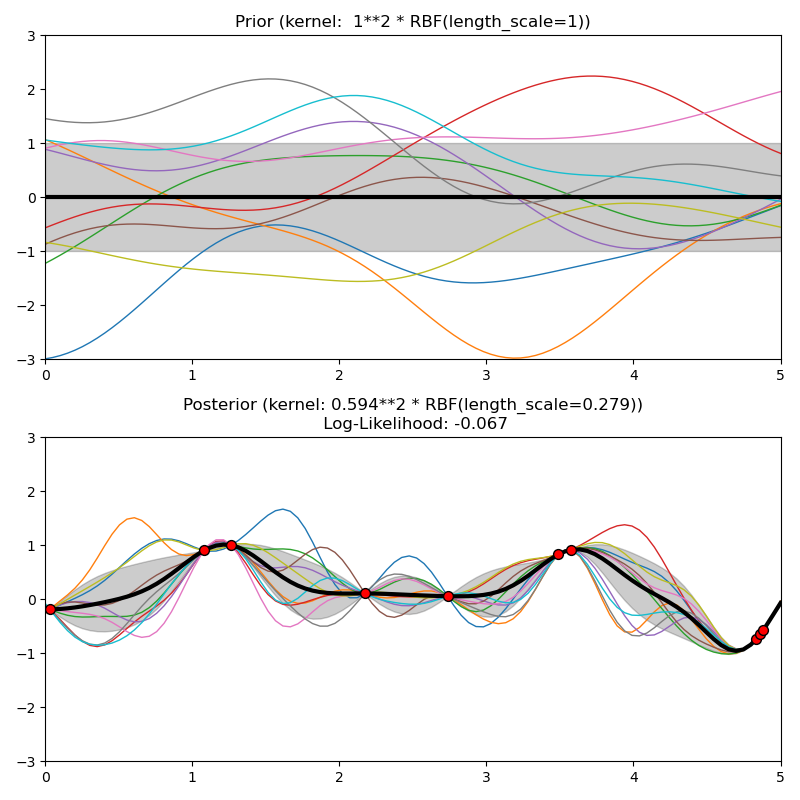
El núcleo RBF es un núcleo estacionario. También se conoce como núcleo «exponencial cuadrado». Está parametrizado por un parámetro de escala de longitud \(l>0\), que puede ser un escalar (variante isotrópica del núcleo) o un vector con el mismo número de dimensiones que las entradas \(x\) (variante anisotrópica del núcleo). El núcleo viene dado por:

\[k(x_i, x_j) = \text{exp}\left(- \frac{d(x_i, x_j)^2}{2l^2} \right)\]

donde \(d(\cdot, \cdot)\) es la distancia euclidiana. Este kernel es infinitamente diferenciable, lo que implica que los GP con este kernel como función de covarianza tienen derivadas cuadráticas medias de todos los órdenes, y por tanto resultan muy suavizadas (smooth). En la siguiente figura se muestran las distribuciones a priori y a posteriori de un GP resultante de un kernel RBF:

1.7.5.5. Núcleo Matérn

El núcleo Matern es un núcleo estacionario y una generalización del núcleo RBF. Tiene un parámetro adicional \(\nu\) que controla la suavidad de la función resultante. Está parametrizado por un parámetro de escala de longitud \(l>0\), que puede ser un escalar (variante isotrópica del núcleo) o un vector con el mismo número de dimensiones que las entradas \(x\) (variante anisotrópica del núcleo). El núcleo viene dado por:

\[k(x_i, x_j) = \frac{1}{\Gamma(\nu)2^{\nu-1}}\Bigg(\frac{\sqrt{2\nu}}{l} d(x_i , x_j )\Bigg)^\nu K_\nu\Bigg(\frac{\sqrt{2\nu}}{l} d(x_i , x_j )\Bigg),\]

donde \(d(\cdot,\cdot)\) es la distancia euclidiana, \(K_\nu(\cdot)\) es una función de Bessel modificada y \(\Gamma(\cdot)\) es la función gamma. Como \(\nu\rightarrow\infty\), el núcleo Matérn converge al núcleo RBF. Cuando \(\nu = 1/2\), el núcleo de Matérn se vuelve idéntico al núcleo exponencial absoluto, es decir

\[k(x_i, x_j) = \exp \Bigg(- \frac{1}{l} d(x_i , x_j ) \Bigg) \quad \quad \nu= \tfrac{1}{2}\]

En particular, \(\nu = 3/2\):

\[k(x_i, x_j) = \Bigg(1 + \frac{\sqrt{3}}{l} d(x_i , x_j )\Bigg) \exp \Bigg(-\frac{\sqrt{3}}{l} d(x_i , x_j ) \Bigg) \quad \quad \nu= \tfrac{3}{2}\]

and \(\nu = 5/2\):

\[k(x_i, x_j) = \Bigg(1 + \frac{\sqrt{5}}{l} d(x_i , x_j ) +\frac{5}{3l} d(x_i , x_j )^2 \Bigg) \exp \Bigg(-\frac{\sqrt{5}}{l} d(x_i , x_j ) \Bigg) \quad \quad \nu= \tfrac{5}{2}\]

son opciones populares para funciones de aprendizaje que no son infinitamente diferenciables (como asume el núcleo RBF), pero al menos una vez (\(\nu = 3/2\)) o dos veces diferenciables (\(\nu = 5/2\)).

La flexibilidad de controlar la suavidad de la función aprendida a través de \(\nu\) permite adaptarse a las propiedades de la verdadera relación funcional subyacente. En la siguiente figura se muestran las distribuciones a priori y a posteriori de un GP resultante de un núcleo Matérn:

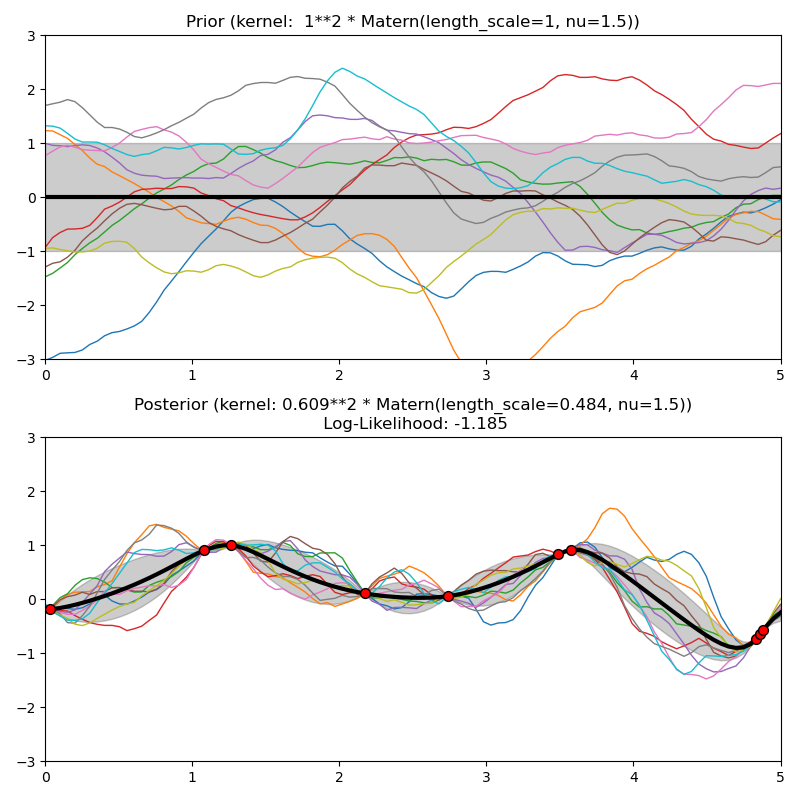
Ver [RW2006], pp84 para más detalles sobre las diferentes variantes del núcleo de Matérn.

1.7.5.6. Núcleo cuadrático racional

El núcleo RationalQuadratic puede verse como una mezcla de escalas (una suma infinita) de núcleos RBF con diferentes escalas de longitud características. Está parametrizado por un parámetro de escala de longitud \(l>0\) y un parámetro de mezcla de escalas \(alpha>0\) Por el momento sólo se admite la variante isotrópica en la que \(l\) es un escalar. El núcleo viene dado por:

\[k(x_i, x_j) = \left(1 + \frac{d(x_i, x_j)^2}{2\alpha l^2}\right)^{-\alpha}\]

En la siguiente figura se muestran las distribuciones a priori y a posteriori de un GP resultante de un kernel RationalQuadratic:

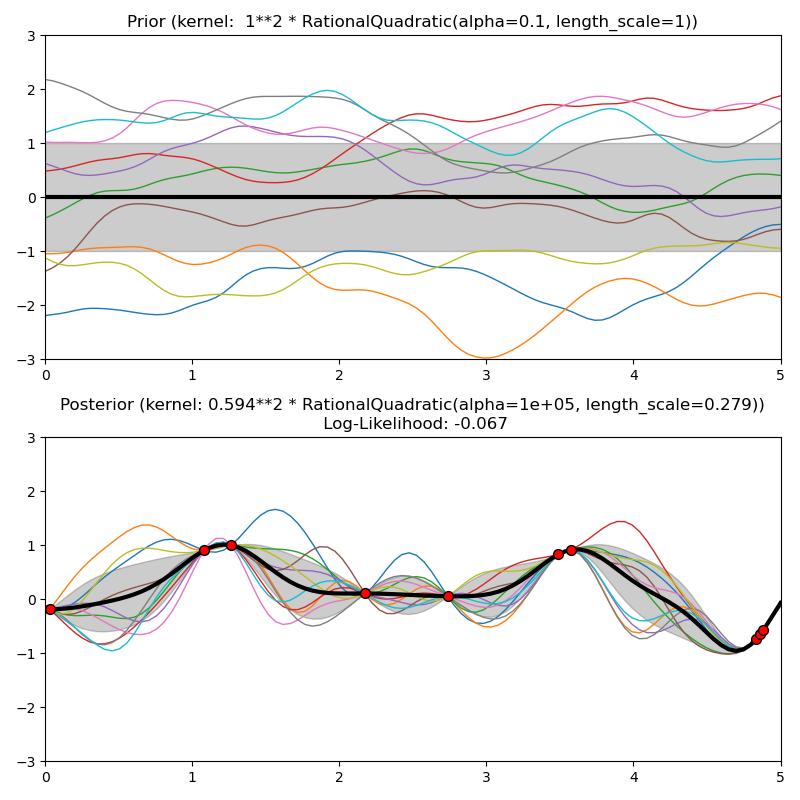
1.7.5.7. Núcleo exponencial sinusoidal cuadrático

El núcleo ExpSineSquared permite modelar funciones periódicas. Está parametrizado por un parámetro de escala de longitud \(l>0\) y un parámetro de periodicidad \(p>0\). Sólo la variante isotrópica donde \(l\) es un escalar es soportada por el momento. El núcleo viene dado por:

\[k(x_i, x_j) = \text{exp}\left(- \frac{ 2\sin^2(\pi d(x_i, x_j) / p) }{ l^ 2} \right)\]

Las distribuciones a priori y a posteriori de un GP resultante de un kernel ExpSineSquared se muestran en la siguiente figura:

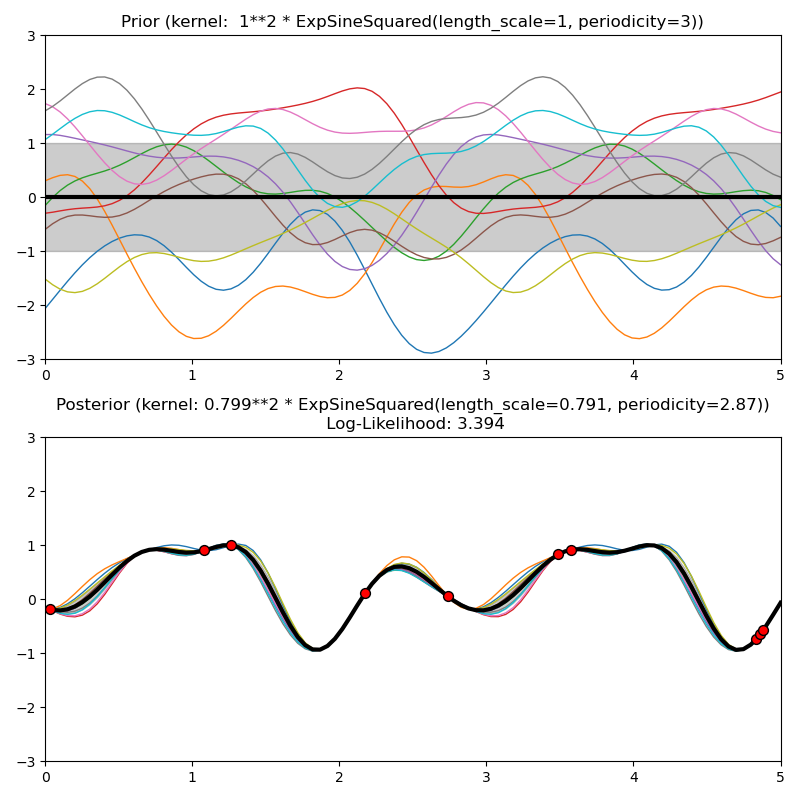
1.7.5.8. Núcleo de producto punto

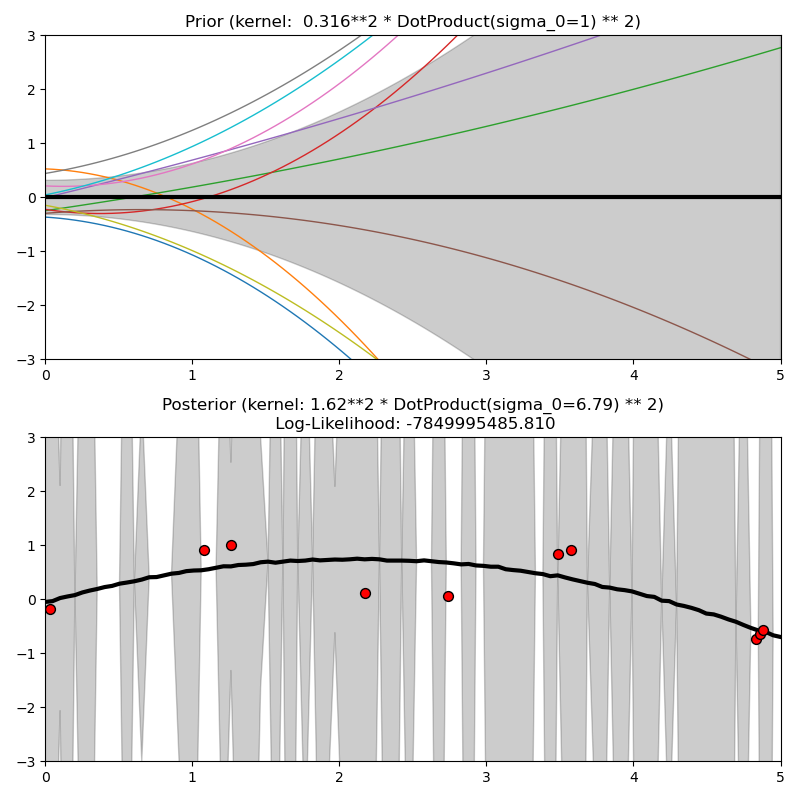
El núcleo DotProduct no es estacionario y puede obtenerse a partir de la regresión lineal poniendo las distribuciones a priori (priors) \(N(0, 1)\) en los coeficientes de \(x_d (d = 1, . . , D)\) y una distribución a priori \(N(0, \sigma_0^2)\) en el sesgo. El núcleo DotProduct es invariante a una rotación de las coordenadas sobre el origen, pero no a las traslaciones. Está parametrizado por un parámetro \(\sigma_0^2\). Para \(\sigma_0^2 = 0\), el núcleo se denomina núcleo lineal homogéneo, en caso contrario es no homogéneo. El núcleo viene dado por

\[k(x_i, x_j) = \sigma_0 ^ 2 + x_i \cdot x_j\]

El núcleo DotProduct se combina habitualmente con la exponenciación. Un ejemplo con exponente 2 se muestra en la siguiente figura:

1.7.5.9. Referencias

RW2006(1,2,3,4,5,6)

Carl Eduard Rasmussen y Christopher K.I. Williams, «Gaussian Processes for Machine Learning», MIT Press 2006, Vínculo al PDF completo y versión oficial del libro aquí .

Duv2014

David Duvenaud, «The Kernel Cookbook: Advice on Covariance functions», 2014, Link .