1.12. Algoritmos multiclase y multisalida

Esta sección de la guía del usuario cubre la funcionalidad relacionada con los problemas de aprendizaje múltiple, incluyendo multiclase, multilabel, y multioutput clasificación y regresión.

Los módulos de esta sección implementan meta-estimators, que requieren que se proporcione un estimador base en su constructor. Los metaestimadores extienden la funcionalidad del estimador base para soportar problemas de aprendizaje múltiple, lo que se consigue transformando el problema de aprendizaje múltiple en un conjunto de problemas más simples, y luego ajustando un estimador por problema.

Esta sección cubre dos módulos: sklearn.multiclass y sklearn.multioutput. El siguiente gráfico muestra los tipos de problemas de los que se encarga cada módulo y los correspondientes metaestimadores que proporciona cada módulo.

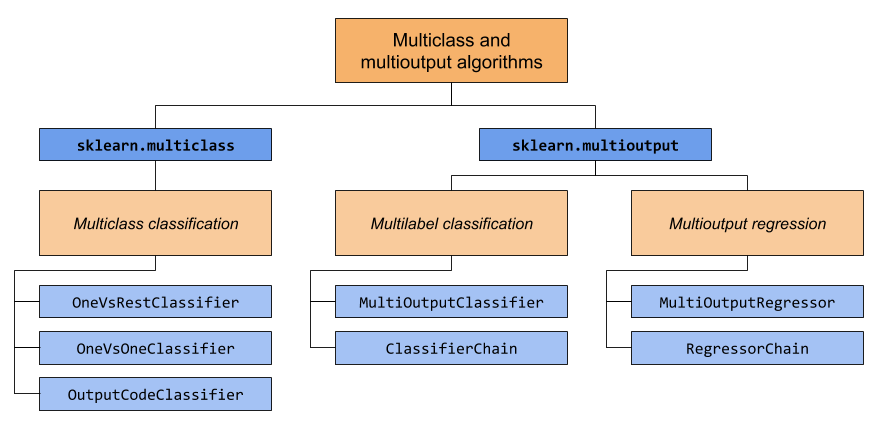
../_images/multi_org_chart.png

La siguiente tabla proporciona una referencia rápida sobre las diferencias entre los tipos de problemas. Se pueden encontrar explicaciones más detalladas en las secciones posteriores de esta guía.

Número de objetivos

Cardinalidad del objetivo

Valid type_of_target

Clasificación multiclase

1

>2

“multiclase”

Clasificación multietiqueta

>1

2 (0 o 1)

“multilabel-indicator”

Clasificación multiclase y multisalida

>1

>2

“multiclase de salida múltiple”

Regresión de salida múltiple

>1

Continuo

“Salida múltiple continua”

A continuación se muestra un resumen de los estimadores de scikit-learn que tienen soporte de aprendizaje múltiple incorporado, agrupados por estrategia. No necesitas los metaestimadores proporcionados por esta sección si estas utilizando uno de estos estimadores. Sin embargo, los meta-estimadores pueden proporcionar estrategias adicionales más allá de lo que está incorporado:

1.12.1. Clasificación multiclase

Advertencia

Todos los clasificadores en scikit-learn hacen la clasificación multiclase inmediata. No es necesario utilizar el módulo sklearn.multiclass a menos que quieras experimentar con diferentes estrategias multiclase.

La clasificación multiclase es una tarea de clasificación con más de dos clases. Cada muestra sólo puede ser etiquetada como una clase.

Por ejemplo, la clasificación mediante características extraídas de un conjunto de imágenes de fruta, donde cada imagen puede ser de una naranja, una manzana o una pera. Cada imagen es una muestra y se etiqueta como una de las 3 clases posibles. La clasificación multiclase parte de la base de que cada muestra se asigna a una sola etiqueta: una muestra no puede ser, por ejemplo, una pera y una manzana.

Aunque todos los clasificadores de scikit-learn son capaces de realizar una clasificación multiclase, los metaestimadores ofrecidos por sklearn.multiclass permiten cambiar la forma en que manejan más de dos clases porque esto puede tener un efecto en el rendimiento del clasificador (ya sea en términos de error de generalización o de recursos computacionales requeridos).

1.12.1.1. Formato del objetivo

Representaciones válidas de multiclase para type_of_target (y) son:

  • Vector de 1d o columna que contiene más de dos valores discretos. Un ejemplo de vector y para 4 muestras:

    >>> import numpy as np
>>> y = np.array(['apple', 'pear', 'apple', 'orange'])
>>> print(y)
['apple' 'pear' 'apple' 'orange']

  • Matriz binary densa o dispersa de forma (n_muestras, n_clases) con una sola muestra por fila, donde cada columna representa una clase. Un ejemplo de matriz binary densa y dispersa para 4 muestras, donde las columnas, en orden, son manzana, naranja y pera:

    >>> import numpy as np
>>> from sklearn.preprocessing import LabelBinarizer
>>> y = np.array(['apple', 'pear', 'apple', 'orange'])
>>> y_dense = LabelBinarizer().fit_transform(y)
>>> print(y_dense)
  [[1 0 0]
   [0 0 1]
   [1 0 0]
   [0 1 0]]
>>> from scipy import sparse
>>> y_sparse = sparse.csr_matrix(y_dense)
>>> print(y_sparse)
    (0, 0)        1
    (1, 2)        1
    (2, 0)        1
    (3, 1)        1

Para más información sobre LabelBinarizer, consulta Transformación del objetivo de predicción (y).

1.12.1.2. Clasificador One Vs Rest

La estrategia one-vs-rest, también conocida como uno-vs-todo, se implementa en OneVsRestClassifier. La estrategia consiste en ajustar un clasificador por clase. Para cada clasificador, la clase se ajusta contra todas las demás clases. Además de su eficiencia computacional (sólo se necesitan clasificadores n_clases), una ventaja de este enfoque es su interpretabilidad. Dado que cada clase está representada por uno y sólo un clasificador, es posible obtener conocimientos sobre la clase inspeccionando su clasificador correspondiente. Esta es la estrategia más comúnmente utilizada y es una elección justa por defecto.

A continuación hay un ejemplo de aprendizaje multiclase usando OvR:

>>> from sklearn import datasets
>>> from sklearn.multiclass import OneVsRestClassifier
>>> from sklearn.svm import LinearSVC
>>> X, y = datasets.load_iris(return_X_y=True)
>>> OneVsRestClassifier(LinearSVC(random_state=0)).fit(X, y).predict(X)
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 1, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])

OneVsRestClassifier también soporta clasificación multietiqueta. Para utilizar esta función, alimentar el clasificador una matriz indicadora, en la que la célula [i, j] indica la presencia de la etiqueta j en la muestra i.

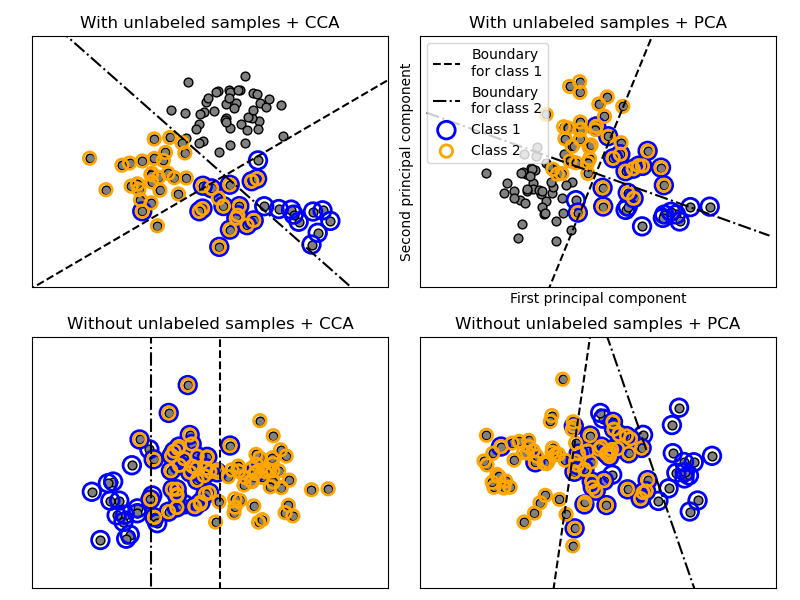
../_images/sphx_glr_plot_multilabel_001.png

Ejemplos:

1.12.1.3. Clasificador OneVsOne

OneVsOneClassifier construye un clasificador por cada par de clases. En el momento de la predicción, se selecciona la clase que ha recibido más votos. En caso de empate (entre dos clases con el mismo número de votos), selecciona la clase con la mayor confianza de clasificación agregada mediante la suma de los niveles de confianza de clasificación por pares calculados por los clasificadores binarios subyacentes.

Dado que requiere ajustar los clasificadores n_classes * (n_classes - 1) / 2, este método suele ser más lento que el de one-vs-the-rest, debido a su complejidad O(n_classes^2). Sin embargo, este método puede ser ventajoso para algoritmos como los algoritmos núcleo que no escalan bien con n_samples. Esto se debe a que cada problema de aprendizaje individual sólo implica un pequeño subconjunto de los datos, mientras que, con one-vs-the-rest, el conjunto de datos completo se utiliza n_classes veces. La función de decisión es el resultado de una transformación monótona de la clasificación uno contra uno.

A continuación hay un ejemplo de aprendizaje multiclase usando OvO:

>>> from sklearn import datasets
>>> from sklearn.multiclass import OneVsOneClassifier
>>> from sklearn.svm import LinearSVC
>>> X, y = datasets.load_iris(return_X_y=True)
>>> OneVsOneClassifier(LinearSVC(random_state=0)).fit(X, y).predict(X)
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 2, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])

Referencias:

  • «Pattern Recognition and Machine Learning. Springer», Christopher M. Bishop, page 183, (First Edition)

1.12.1.4. Clasificador de Código de salida

Las estrategias basadas en códigos de salida con corrección de errores son bastante diferentes a las de one-vs-the-rest y one-vs-one. Con estas estrategias, cada clase se representa en un espacio euclidiano, donde cada dimensión sólo puede ser 0 o 1. Otra forma de decirlo es que cada clase está representada por un código binario (un arreglo de 0 y 1). La matriz que lleva la cuenta de la ubicación/código de cada clase se llama libro de códigos. El tamaño del código es la dimensionalidad del espacio mencionado. Intuitivamente, cada clase debería estar representada por un código lo más único posible y un buen libro de códigos debería estar diseñado para optimizar la precisión de la clasificación. En esta implementación, simplemente utilizamos un libro de códigos generado aleatoriamente como se recomienda en 3 aunque se pueden añadir métodos más elaborados en el futuro.

En el momento del ajuste, se ajusta un clasificador binario por cada bit del libro de códigos. En el momento de la predicción, los clasificadores se utilizan para proyectar nuevos puntos en el espacio de clases y se elige la clase más cercana a los puntos.

En OutputCodeClassifier, el atributo code_size permite al usuario controlar el número de clasificadores que se utilizarán. Es un porcentaje del número total de clases.

Un número entre 0 y 1 requerirá menos clasificadores que one-vs-the-rest. En teoría, log2(n_clases) / n_clases es suficiente para representar cada clase de forma inequívoca. Sin embargo, en la práctica, puede que no se consiga una buena precisión, ya que log2(n_clases) es mucho menor que n_clases.

Un número superior a 1 requerirá más clasificadores que one-vs-the-rest. En este caso, algunos clasificadores corregirán en teoría los errores cometidos por otros clasificadores, de ahí el nombre de «corrección de errores». En la práctica, sin embargo, esto puede no ocurrir, ya que los errores de los clasificadores suelen estar correlacionados. Los códigos de salida con corrección de errores tienen un efecto similar al del empaquetado.

A continuación hay un ejemplo de aprendizaje multiclase utilizando Codigos de Salida:

>>> from sklearn import datasets
>>> from sklearn.multiclass import OutputCodeClassifier
>>> from sklearn.svm import LinearSVC
>>> X, y = datasets.load_iris(return_X_y=True)
>>> clf = OutputCodeClassifier(LinearSVC(random_state=0),
...                            code_size=2, random_state=0)
>>> clf.fit(X, y).predict(X)
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1,
       1, 2, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 2, 2, 2, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 1, 1, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])

Referencias:

  • «Solving multiclass learning problems via error-correcting output codes», Dietterich T., Bakiri G., Journal of Artificial Intelligence Research 2, 1995.

3

«The error coding method and PICTs», James G., Hastie T., Journal of Computational and Graphical statistics 7, 1998.

  • «The Elements of Statistical Learning», Hastie T., Tibshirani R., Friedman J., page 606 (second-edition) 2008.

1.12.2. Clasificación multietiqueta

La clasificación multietiqueta (estrechamente relacionada con la clasificación de salidas múltiples**) es una tarea de clasificación que etiqueta cada muestra con «m» etiquetas de «n_classes» clases posibles, donde «m» puede ser de 0 a «n_classes» inclusive. Esto puede considerarse como la predicción de propiedades de una muestra que no son mutuamente excluyentes. Formalmente, se asigna una salida binaria a cada clase, para cada muestra. Las clases positivas se indican con 1 y las negativas con 0 o -1. Por lo tanto, es comparable a la ejecución de tareas de clasificación binaria n_classes, por ejemplo con MultiOutputClassifier. Este enfoque trata cada etiqueta de forma independiente, mientras que los clasificadores multietiqueta pueden tratar las múltiples clases simultáneamente, teniendo en cuenta el comportamiento correlacionado entre ellas.

Por ejemplo, la predicción de los temas relevantes para un documento de texto o un vídeo. El documento o el vídeo puede tratar de una de las clases de temas «religión», «política», «finanzas» o «educación», de varias de las clases de temas o de todas las clases de temas.

1.12.2.1. Formato del objetivo

Una representación válida de multilabel y es una matriz binary densa o dispersa de la forma (n_samples, n_classes). Cada columna representa una clase. Los 1 de cada fila denotan las clases positivas con las que se ha etiquetado una muestra. Un ejemplo de matriz densa y para 3 muestras:

>>> y = np.array([[1, 0, 0, 1], [0, 0, 1, 1], [0, 0, 0, 0]])
>>> print(y)
[[1 0 0 1]
 [0 0 1 1]
 [0 0 0 0]]

También se pueden crear matrices binarias densas usando MultiLabelBinarizer. Para obtener más información, consulta Transformación del objetivo de predicción (y).

Un ejemplo del mismo y en forma de matriz dispersa:

>>> y_sparse = sparse.csr_matrix(y)
>>> print(y_sparse)
  (0, 0)      1
  (0, 3)      1
  (1, 2)      1
  (1, 3)      1

1.12.2.2. Clasificador de salidas múltiples

Se puede añadir soporte de clasificación multietiqueta a cualquier clasificador con MultiOutputClassifier. Esta estrategia consiste en ajustar un clasificador por objetivo. Esto permite múltiples clasificaciones de variables objetivo. El propósito de esta clase es extender los estimadores para poder estimar una serie de funciones objetivo (f1,f2,f3…,fn) que se entrenan en una única matriz de predicción X para predecir una serie de respuestas (y1,y2,y3…,yn).

A continuación se muestra un ejemplo de clasificación multietiqueta:

>>> from sklearn.datasets import make_classification
>>> from sklearn.multioutput import MultiOutputClassifier
>>> from sklearn.ensemble import RandomForestClassifier
>>> from sklearn.utils import shuffle
>>> import numpy as np
>>> X, y1 = make_classification(n_samples=10, n_features=100, n_informative=30, n_classes=3, random_state=1)
>>> y2 = shuffle(y1, random_state=1)
>>> y3 = shuffle(y1, random_state=2)
>>> Y = np.vstack((y1, y2, y3)).T
>>> n_samples, n_features = X.shape # 10,100
>>> n_outputs = Y.shape[1] # 3
>>> n_classes = 3
>>> forest = RandomForestClassifier(random_state=1)
>>> multi_target_forest = MultiOutputClassifier(forest, n_jobs=-1)
>>> multi_target_forest.fit(X, Y).predict(X)
array([[2, 2, 0],
       [1, 2, 1],
       [2, 1, 0],
       [0, 0, 2],
       [0, 2, 1],
       [0, 0, 2],
       [1, 1, 0],
       [1, 1, 1],
       [0, 0, 2],
       [2, 0, 0]])

1.12.2.3. Cadena clasificadora

Las cadenas de clasificadores (ver ClassifierChain) son una forma de combinar varios clasificadores binarios en un único modelo multietiqueta que es capaz de explotar las correlaciones entre objetivos.

Para un problema de clasificación multietiqueta con N clases, a N clasificadores binarios se les asigna un número entero entre 0 y N-1. Estos enteros definen el orden de los modelos en la cadena. A continuación, cada clasificador se ajusta a los datos de entrenamiento disponibles más las etiquetas verdaderas de las clases a cuyos modelos se les asignó un número inferior.

Cuando se predice, las etiquetas verdaderas no estarán disponibles. En su lugar, las predicciones de cada modelo se transmiten a los modelos posteriores de la cadena que se usarán como características.

Es evidente que el orden de la cadena es importante. El primer modelo en la cadena no tiene información sobre las otras etiquetas, mientras que el último modelo en la cadena tiene características que indican la presencia de todas las demás etiquetas. En general, uno no sabe el orden óptimo de los modelos en la cadena, por lo que típicamente muchas cadenas ordenadas aleatoriamente son ajustadas y sus predicciones son promediadas juntas.

Referencias:

Jesse Read, Bernhard Pfahringer, Geoff Holmes, Eibe Frank,

«Classifier Chains for Multi-label Classification», 2009.

1.12.3. Clasificación multiclase y multisalida

La clasificación multiclase de salida múltiple (también conocida como clasificación multitarea) es una tarea de clasificación que etiqueta cada muestra con un conjunto de propiedades no binarias. Tanto el número de propiedades como el número de clases por propiedad es superior a 2. Así, un único estimador se encarga de varias tareas de clasificación conjuntas. Se trata tanto de una generalización de la tarea de clasificación de múltiples etiquetas, que sólo considera atributos binarios, como de una generalización de la tarea de clasificación de múltiples clases, en la que sólo se considera una propiedad.

Por ejemplo, la clasificación de las propiedades «tipo de fruta» y «color» para un conjunto de imágenes de frutas. La propiedad «tipo de fruta» tiene las clases posibles «manzana», «pera» y «naranja». La propiedad «color» tiene las clases posibles: «verde», «rojo», «amarillo» y «naranja». Cada muestra es una imagen de una fruta, se emite una etiqueta para ambas propiedades y cada etiqueta es una de las posibles clases de la propiedad correspondiente.

Observa que todos los clasificadores que manejan tareas multiclase de salidos múltiples (también conocidas como clasificación multitarea), admiten la tarea de clasificación multietiqueta como un caso especial. La clasificación multitarea es similar a la tarea de clasificación de salidas múltiples con diferentes formulaciones del modelo. Para más información, consulta la documentación del estimador correspondiente.

Advertencia

Actualmente, ninguna métrica en sklearn.metrics soporta la tarea de clasificación multiclase de salida múltiple.

1.12.3.1. Formato del objetivo

Una representación válida de multioutput y es una matriz densa de forma (n_samples, n_classes) de etiquetas de clase. Es una concatenación por columnas de 1d variables de multiclass. Un ejemplo de y para 3 muestras:

>>> y = np.array([['apple', 'green'], ['orange', 'orange'], ['pear', 'green']])
>>> print(y)
[['apple' 'green']
 ['orange' 'orange']
 ['pear' 'green']]

1.12.4. Regresión de salida múltiple

La ** Rgresión de salida múltiple** predice múltiples propiedades numéricas para cada muestra. Cada propiedad es una variable numérica y el número de propiedades a predecir para cada muestra es mayor o igual a 2. Algunos estimadores que soportan la regresión de salida múltiple son más rápidos que la simple ejecución de estimadores n_output.

Por ejemplo, predicción tanto de la velocidad del viento como de la dirección del viento, en grados, utilizando datos obtenidos en una determinada ubicación. Cada muestra sería información obtenida en una ubicación y tanto la velocidad del viento como la dirección serían salida para cada muestra.

1.12.4.1. Formato del objetivo

Una representación válida de multioutput y es una matriz densa de la forma (n_samples, n_classes) de flotantes. Una concatenación sabia de columna de variables continuous. Un ejemplo de y para 3 muestras:

>>> y = np.array([[31.4, 94], [40.5, 109], [25.0, 30]])
>>> print(y)
[[ 31.4  94. ]
 [ 40.5 109. ]
 [ 25.   30. ]]

1.12.4.2. Regresor de salida múltiples

El soporte de regresión de salidas múltplies puede añadirse a cualquier regresor con MultiOutputRegressor. Esta estrategia consiste en ajustar un regresor por objetivo. Dado que cada objetivo está representado exactamente por un regresor, es posible conocer el objetivo inspeccionando su regresor correspondiente. Como MultiOutputRegressor se ajusta a un regresor por objetivo que no puede aprovechar las correlaciones entre objetivos.

A continuación hay un ejemplo de regresión de salidas múltiples:

>>> from sklearn.datasets import make_regression
>>> from sklearn.multioutput import MultiOutputRegressor
>>> from sklearn.ensemble import GradientBoostingRegressor
>>> X, y = make_regression(n_samples=10, n_targets=3, random_state=1)
>>> MultiOutputRegressor(GradientBoostingRegressor(random_state=0)).fit(X, y).predict(X)
array([[-154.75474165, -147.03498585,  -50.03812219],
       [   7.12165031,    5.12914884,  -81.46081961],
       [-187.8948621 , -100.44373091,   13.88978285],
       [-141.62745778,   95.02891072, -191.48204257],
       [  97.03260883,  165.34867495,  139.52003279],
       [ 123.92529176,   21.25719016,   -7.84253   ],
       [-122.25193977,  -85.16443186, -107.12274212],
       [ -30.170388  ,  -94.80956739,   12.16979946],
       [ 140.72667194,  176.50941682,  -17.50447799],
       [ 149.37967282,  -81.15699552,   -5.72850319]])

1.12.4.3. Cadena de Regresor

Las cadenas de regresores (ver RegressorChain) son análogas a ClassifierChain como forma de combinar una serie de regresiones en un único modelo multiobjetivo que es capaz de explotar las correlaciones entre los objetivos.