1.11. Métodos combinados

Los métodos combinados se utilizan para unir las predicciones de varios estimadores base construidos desde un algoritmo de aprendizaje dado con el propósito de tener una generalización / robustez mayor que la de un solo estimador.

Se suelen distinguir dos familias de métodos combinados:

• En los métodos de promedio, el principio guía es la creación de varios estimadores independientes para después promediar sus predicciones. En promedio, el estimador combinado es mejor que cualquiera de los estimadores base individuales porque su varianza se reduce.

  Ejemplos: Métodos de bagging, Bosques de árboles aleatorios, …

• En cambio, en los métodos de boosting, los estimadores base se construyen de manera secuencial y uno intenta reducir el sesgo del estimador combinado. La intención es producir un conjunto potente a partir de varios modelos débiles.

  Ejemplos: AdaBoost, Gradient Tree Boosting, …

1.11.1. Metaestimador de bagging

En los algoritmos de conjunto, los métodos de bagging forman una clase de algoritmos que construyen varias instancias de un estimador de caja negra en subconjuntos aleatorios del conjunto de entrenamiento original y luego agregan sus predicciones individuales para realizar una predicción final. Estos métodos introducen la aleatorización en la construcción de un estimador base (por ejemplo, un árbol de decisión) y crean un conjunto después para así reducir su varianza. En muchos casos, los métodos de bagging son una manera muy sencilla de mejorar con respecto a un único modelo, sin hacer necesario el adaptar el algoritmo base subyacente. Como proporcionan una forma de reducir el sobreajuste, los métodos de bagging funcionan mejor con modelos fuertes y complejos (por ejemplo, árboles de decisión completamente desarrollados), al contrario que los métodos de boosting, los cuales suelen funcionar mejor con modelos débiles (por ejemplo, árboles de decisión con poca profundidad).

Los métodos de bagging vienen en muchos sabores, pero por lo general difieren uno del otro por la forma en la cual agarran subconjuntos aleatorios del conjunto de entrenamiento:

• Cuando se escogen subconjuntos aleatorios del conjunto de datos como subconjuntos aleatorios de las muestras, este algoritmo es conocido como Pasting [B1999].

• Cuando las muestras son escogidas con reemplazo, entonces el método es conocido como Bagging [B1996].

• Cuando son escogidos subconjuntos aleatorios del conjunto de datos como subconjuntos aleatorios de las características, entonces el método se conoce como Random Subspaces [H1998].

• Finalmente, cuando los estimadores base son construidos en subconjuntos tanto de características como muestras, entonces el método es conocido como Random Patches [LG2012].

En scikit-learn, los métodos de bagging son ofrecidos como un metaestimador unificado BaggingClassifier (resp. BaggingRegressor) tomando como entrada un estimador base especificado por el usuario y parámetros especificando la estrategia a utilizar para escoger subconjuntos aleatorios. En particular. max_samples y max_features controlan el tamaño de los subconjuntos (en términos de muestras y características), mientras que bootstrap and bootstrap_features controlan si las muestras y características son escogidas con o sin reemplazo. Cuando es utilizado un subconjunto de las muestras disponibles, la exactitud de la generalización puede ser estimada con las muestras out-of-bag estableciendo que oob_score=True. Como un ejemplo, el fragmento de código abajo ilustra como instanciar un conjunto de bagging de KNeighborsClassifier estimadores base, cada uno construido con subconjuntos aleatorios de 50% de las muestras y 50% de las características.

>>> from sklearn.ensemble import BaggingClassifier
>>> from sklearn.neighbors import KNeighborsClassifier
>>> bagging = BaggingClassifier(KNeighborsClassifier(),
...                             max_samples=0.5, max_features=0.5)

Ejemplos:

• Estimador único frente a empaquetado (bagging): descomposición sesgo-varianza

Referencias

B1999

L. Breiman, «Pasting small votes for classification in large databases and on-line», Machine Learning, 36(1), 85-103, 1999.

B1996

L. Breiman, «Bagging predictors», Machine Learning, 24(2), 123-140, 1996.

H1998

T. Ho, «The random subspace method for constructing decision forests», Pattern Analysis and Machine Intelligence, 20(8), 832-844, 1998.

LG2012

G. Louppe and P. Geurts, «Ensembles on Random Patches», Machine Learning and Knowledge Discovery in Databases, 346-361, 2012.

1.11.2. Bosques de árboles aleatorios

El módulo sklearn.ensemble incluye dos algoritmos de promedio basados en arboles de decisión: el algoritmo RandomForest y el método Extra-Trees. Ambos algoritmos son técnicas de perturbar-y-combinar [B1998] específicamente diseñadas para árboles. Esto significa que un diverso conjunto de clasificadores es creado introduciendo aleatoriedad en la construcción de los clasificadores. La predicción del conjunto es dada como la predicción promediada de los clasificadores individuales.

Como otros clasificadores, los clasificadores de árboles tienen que estar provistos con dos arreglos: un arreglo X denso o disperso de forma (n_samples, n_features), sosteniendo las muestras de entrenamiento, y un arreglo Y de forma (n_samples,), sosteniendo los valores objetivo (etiquetas de clase) para las muestras de entrenamiento:

>>> from sklearn.ensemble import RandomForestClassifier
>>> X = [[0, 0], [1, 1]]
>>> Y = [0, 1]
>>> clf = RandomForestClassifier(n_estimators=10)
>>> clf = clf.fit(X, Y)

Como los arboles de decisión, los bosques de arboles también se extienden a problemas de salida múltiple (si Y es un array de forma (n_samples, n_outputs)).

1.11.2.1. Bosques Aleatorios

En los bosques aleatorios (ver las clases RandomForestClassifier y RandomForestRegressor), cada árbol en el conjunto es construido desde una muestra escogida con reemplazo (es decir, una muestra de bootstrap) desde el conjunto de entrenamiento.

Además, cuando se divide cada nodo durante la construcción de un árbol, se encuentra la mejor división desde todas las características de entrada o bien desde un subconjunto aleatorio de tamaño max_features. (Ver las pautas de ajuste de parámetros para más detalles).

Estas dos fuentes de aleatoriedad son utilizadas para disminuir la varianza del estimador de árbol. En efecto, los árboles de decisión únicos suelen exhibir varianza alta y tienden a sobreajustarse. Al inyectar aleatoriedad en los bosques, se obtienen árboles con errores de predicción algo desacoplados. Algunos de estos errores se pueden cancelar tomando un promedio de estas predicciones. Los bosques aleatorios consiguen una varianza reducida mediante la combinación de árboles diversos, a veces al costo de un ligero aumento en el sesgo. En la practica, la reducción de varianza suele ser significativa, por lo que se obtiene un mejor modelo en general.

A diferencia de la publicación original [B2001], la implementación de scikit-learn combina clasificadores al promediar su predicción probabilística, en lugar de dejar que cada clasificador vote por una única clase.

1.11.2.2. Árboles extremadamente aleatorizados

En árboles extremadamente aleatorizados (ver las clases ExtraTreesClassifier y ExtraTreesRegressor), la aleatoriedad va un paso más allá en la forma en la que se calculan las divisiones. Como en los bosques aleatorios, un subconjunto aleatorio de características candidato son utilizadas, pero en lugar de buscar por los umbrales más discriminatorios, los umbrales son escogidos de forma aleatoria por cada característica candidato, y se escoge el mejor de estos umbrales generados al azar como la regla según la cual se realizaran las divisiones. Esto usualmente permite reducir la varianza del modelo un poco más, al costo de un ligeramente mayor aumento en el sesgo:

>>> from sklearn.model_selection import cross_val_score
>>> from sklearn.datasets import make_blobs
>>> from sklearn.ensemble import RandomForestClassifier
>>> from sklearn.ensemble import ExtraTreesClassifier
>>> from sklearn.tree import DecisionTreeClassifier

>>> X, y = make_blobs(n_samples=10000, n_features=10, centers=100,
...     random_state=0)

>>> clf = DecisionTreeClassifier(max_depth=None, min_samples_split=2,
...     random_state=0)
>>> scores = cross_val_score(clf, X, y, cv=5)
>>> scores.mean()
0.98...

>>> clf = RandomForestClassifier(n_estimators=10, max_depth=None,
...     min_samples_split=2, random_state=0)
>>> scores = cross_val_score(clf, X, y, cv=5)
>>> scores.mean()
0.999...

>>> clf = ExtraTreesClassifier(n_estimators=10, max_depth=None,
...     min_samples_split=2, random_state=0)
>>> scores = cross_val_score(clf, X, y, cv=5)
>>> scores.mean() > 0.999
True

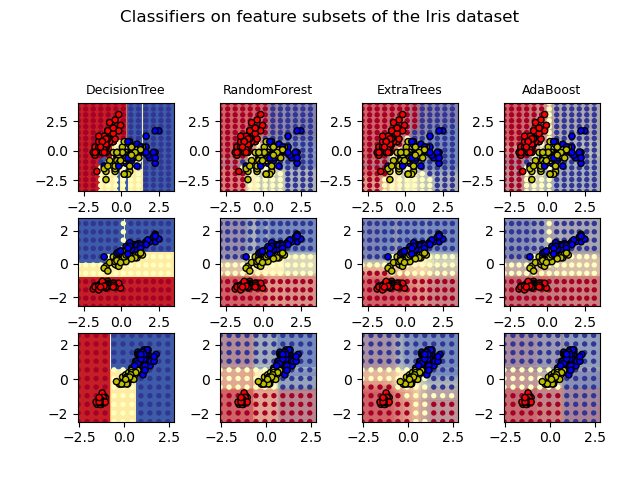
1.11.2.3. Parámetros

Los parámetros principales a ajustar cuando se utilizan estos métodos son n_estimators y max_features. El primero es el número de árboles en el bosque. Mientras más grande, mejor, pero tardará también más tiempo en calcular. Además, ten en cuenta que los resultados dejarán de mejorar significativamente después de un número crítico de árboles. El segundo es el tamaño de los subconjuntos aleatorios de características a considerar cuando se divide un nodo. Reduce la varianza mientras sea más bajo, pero también aumenta el sesgo. Empíricamente, max_features=None (considerar siempre todas las características en lugar de un subconjunto aleatorio), y max_features="sqrt" (usar un subconjunto aleatorio de tamaño sqrt(n_features)) son buenos valores por defecto para problemas de regresión, y tareas de clasificación (donde n_features es el número de características en los datos), respectivamente. Buenos resultados se suelen obtener al establecer que max_depth=None en combinación con min_samples_split=2 (es decir, cuando se desarrollan los árboles por completo). Sin embargo, ten en cuenta que estos valores no suelen ser óptimos, y quizás resulten en modelos que consumen mucha RAM. Los mejores valores de parámetros siempre deben ser validados de forma cruzada. Además, ten en cuenta que en bosques aleatorios, se usan por defecto muestras de bootstrap (bootstrap=True), mientras que usar todo el conjunto de datos (bootstrap=False) es la estrategia por defecto de extra-trees. Cuando se utiliza el muestreo por bootstrap, la exactitud de la generalización puede ser estimada en las muestras que sobren o que queden fuera-de-bolsa (out-of-bag). Esto se puede habilitar estableciendo que oob_score=True.

Nota

Con los parámetros predeterminados, el tamaño del modelo es \(O( M * N * log (N) )\). donde \(M\) es el número de árboles y \(N\) es el número de muestras. Si se desea reducir el tamaño del modelo, se pueden cambiar estos parámetros: min_samples_split, max_leaf_nodes, max_depth y min_samples_leaf.

1.11.2.4. Paralelización

Finalmente, este módulo también permite la construcción en paralelo de los árboles y el cálculo en paralelo de las predicciones mediante el parámetro n_jobs. Si n_jobs=k, entonces los cálculos se dividen en k trabajos, y se ejecutan en k núcleos de la máquina. Si n_jobs=-1, entonces todos los núcleos disponibles en la máquina serán utilizados. Ten en cuenta que, debido a la sobrecarga de la comunicación entre procesos, es posible que la aceleración no será lineal (es decir, usar k trabajos desafortunadamente no sera k veces más rápido). Sin embargo, la aceleración igualmente puede ser significativa cuando se construye un número grande de árboles, o cuando se construye un solo árbol que requiere una buena cantidad de tiempo (por ejemplo, en conjuntos de datos grandes).

Ejemplos:

• Graficar las superficies de decisión de los ensembles de árboles en el conjunto de datos iris

• Importancia de los píxeles con un bosque paralelo de árboles

• Finalización facial con estimadores de salida múltiple

Referencias

B2001

12. Breiman, «Random Forests», Machine Learning, 45(1), 5-32, 2001.

B1998

12. Breiman, «Arcing Classifiers», Annals of Statistics 1998.

• P. Geurts, D. Ernst., and L. Wehenkel, «Extremely randomized trees», Machine Learning, 63(1), 3-42, 2006.

1.11.2.5. Evaluación de importancia de características

El rango relativo (es decir, la profundidad) de una característica usada como nodo de decisión en un árbol puede ser utilizada para estimar la importancia relativa de esa característica con respecto a la previsibilidad de la variable objetivo. Las características usadas en la cima del árbol contribuyen a la decisión final de predicción en una fracción grande de las muestras de entrada. La fracción esperada de las muestras a la cual contribuyen puede entonces ser usada como un estimado de la importancia relativa de las características. En scikit-learn, la fracción de muestras a la cual una característica contribuye es combinada con la reducción en impureza que produce su división para crear una estimación normalizada del poder predictivo de esa característica.

Mediante la promediación de los estimados de habilidad predictiva sobre varios árboles aleatorizados, uno puede reducir la varianza de dicho estimado y usarlo para seleccionar características. Esto se conoce como la disminución media de la impureza, o DMI (MDI, en ingles). Ver [L2014] para más información sobre la DMI y la evaluación de importancia de características con Bosques Aleatorios.

Advertencia

Las importancias de característica basadas en impureza calculadas en modelos basados en árboles sufren de dos defectos clave que pueden llevar a conclusiones no representativas. Primero, son calculados en estadísticas derivadas del conjunto de datos de entrenamiento y por lo tanto no necesariamente nos informan acerca de cuáles características son las más importantes para hacer buenas predicciones en los conjuntos de datos retenidos. Segundo, prefieren características de alta cardinalidad, es decir, características con muchos valores únicos. Importancia de la característica de permutación es una alternativa a la importancia de característica basada en impureza que no sufre de estos defectos. Estos dos métodos para obtener la importancia de características se exploran en: Importancia de la Permutación vs la Importancia de las Características del Bosque Aleatorio (MDI).

El siguiente ejemplo presenta una representación codificada en color de la importancia relativa de cada pixel para una tarea de reconocimiento de caras utilizando un modelo ExtraTreesClassifier.

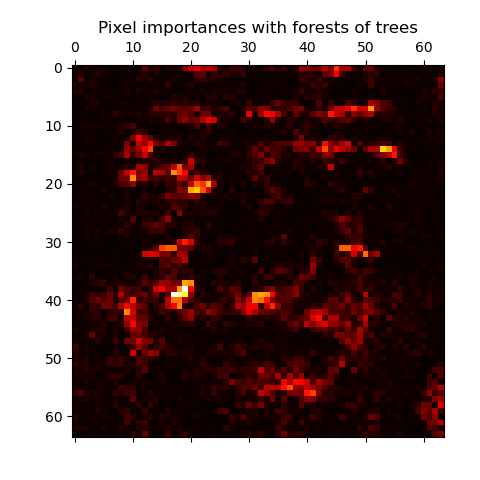
En la práctica, estos estimados se almacenan como un atributo llamado feature_importances_ en el modelo ajustado. Este es un arreglo de forma (n_features,) cuyos valores son positivos y cuya suma resulta en 1.0. Mientras más grande sea el valor, más importante va a ser la contribución de la característica correspondiente a la función de predicción.

Ejemplos:

• Importancia de los píxeles con un bosque paralelo de árboles

• Importancia de las características con los bosques de árboles

Referencias

L2014

G. Louppe, «Understanding Random Forests: From Theory to Practice», PhD Thesis, U. of Liege, 2014.

1.11.2.6. Incrustación de Arboles Totalmente Aleatorios

RandomTreesEmbedding implementa una transformación no supervisada de los datos. Usando un bosque de árboles completamente aleatorios, RandomTreesEmbedding codifica los datos mediante los índices de las hojas en las que termina un punto de datos. Este índice es entonces codificado de una manera one-of-K, dando lugar a una codificación binaria dispersa y de alta dimensión. Esta codificación puede ser eficientemente calculada y después ser usada como una base para otras tareas de aprendizaje. El tamaño y la dispersión del codigo puede ser influenciada eligiendo el número de árboles y la profundidad máxima por árbol. Por cada árbol en el conjunto, la codificación contiene una entrada de uno. El tamaño de la codificación es a lo mas n_estimators * 2 ** max_depth, el número máximo de hojas en el bosque.

Ya que los puntos de datos vecinos son mas probables a estar dentro de la misma hoja de un árbol, la transformación realiza una estimación de densidad implícita y no paramétrica.

Ejemplos:

• Transformación de rasgos de hashing mediante Árboles Totalmente Aleatorios

• Aprendizaje múltiple sobre dígitos manuscritos: Incrustación local lineal, Isomap… compares non-linear dimensionality reduction techniques on handwritten digits.

• Transformaciones de características con grupos (ensembles) de árboles compares supervised and unsupervised tree based feature transformations.

Ver también

Aprendizaje múltiple techniques can also be useful to derive non-linear representations of feature space, also these approaches focus also on dimensionality reduction.

1.11.3. AdaBoost

El módulo sklearn.ensemble incluye el popular algoritmo de boosting AdaBoost, introducido en 1995 por Freund y Schapire [FS1995].

El principio básico de AdaBoost es encajar una secuencia de aprendices débiles (es decir, modelos que solo son ligeramente mejores que adivinar al azar, como los árboles de decisión pequeños) en versiones repetidamente modificadas de los datos. Las predicciones de todos ellos son entonces combinados mediante un voto por mayoría ponderado (o suma) para producir la última predicción. Las modificaciones de datos en cada iteración de boosting consisten en aplicar los ponderados \(w_1\), \(w_2\), …, \(w_N\) a cada una de las muestras de entrenamiento. Inicialmente, esos ponderados son todos establecidos como \(w_i = 1/N\), para que el primer paso simplemente entrene a un aprendiz débil con los datos originales. Para cada iteración sucesiva, los ponderados de la muestra son modificados individualmente y el algoritmo de aprendizaje es aplicado de nuevo a los datos reponderados. En un paso determinado, se incrementan los ponderados de aquellos ejemplos de entrenamiento que fueron predichos incorrectamente por el modelo con boosting inducido en el paso anterior, mientras que los ponderados son disminuidos para aquellos que fueron predichos correctamente. Con cada iteración, los ejemplos que fueron difíciles de predecir reciben influencia cada vez mayor. Cada aprendedor débil subsecuente es entonces forzado a concentrarse en los ejemplos que fueron omitidos por aquellos anteriores en la secuencia [HTF].

AdaBoost puede ser utilizado tanto para problemas de clasificación como de regresión:

• Para clasificación multiclase, AdaBoostClassifier implementa AdaBoost-SAMME y AdaBoost-SAMME.R [ZZRH2009].

• Para la regresión, AdaBoostRegressor implementa AdaBoost.R2 [D1997].

1.11.3.1. Uso

El siguiente ejemplo muestra cómo ajustar un clasificador AdaBoost con 100 aprendices débiles:

>>> from sklearn.model_selection import cross_val_score
>>> from sklearn.datasets import load_iris
>>> from sklearn.ensemble import AdaBoostClassifier

>>> X, y = load_iris(return_X_y=True)
>>> clf = AdaBoostClassifier(n_estimators=100)
>>> scores = cross_val_score(clf, X, y, cv=5)
>>> scores.mean()
0.9...

El número de algoritmos de aprendizaje débiles es controlado por el parámetro n_estimators. El parámetro learning_rate controla la contribución de los algoritmos de aprendizaje débiles en la última combinación. Por defecto, los algoritmos de aprendizaje débiles son tocones de decisión (decision stumps, en inglés). Diferentes algoritmos de aprendizaje débiles pueden ser especificados a través del parámetro base_estimator. Los principales parámetros a ajustar para obtener buenos resultados son n_estimators y la complejidad de los estimadores base (por ejemplo, su profundidad max_depth o el número mínimo requerido de muestras para considerar una división min_samples_split).

Ejemplos:

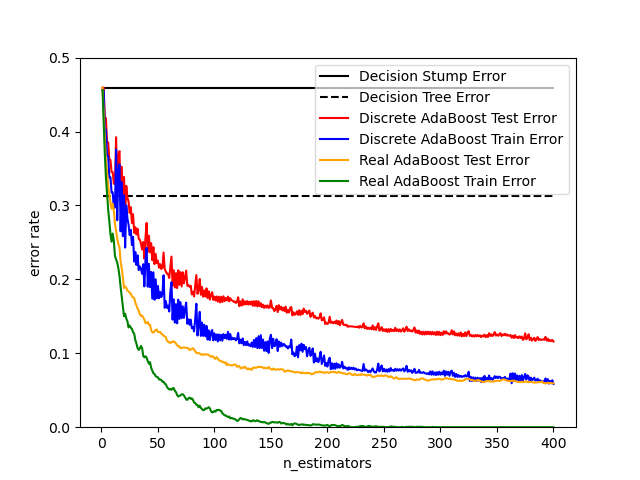
• AdaBoost Discreto versus Real compara el error de clasificación de un tope de decisión, árbol de decisión, y un tope de decisión con boosting usando AdaBoost-SAMME y AdaBoost-SAMME.R.

• Árboles de decisión multiclase AdaBoosted muestra el rendimiento de AdaBoost-SAMME y AdaBoost-SAMME.R en un problema de multiclase.

• AdaBoost de dos clases muestra el límite de decisión y los valores de la función de decisión para un problema de dos clases separables no linealmente usando AdaBoost-SAMME.

• Regresión en árbol de decisión con AdaBoost demuestra regresión con el algoritmo AdaBoost.R2.

Referencias

FS1995

Y. Freund, and R. Schapire, «A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting», 1997.

ZZRH2009

J. Zhu, H. Zou, S. Rosset, T. Hastie. «Multi-class AdaBoost», 2009.

D1997

8. Drucker. «Improving Regressors using Boosting Techniques», 1997.

HTF(1,2,3)

T. Hastie, R. Tibshirani and J. Friedman, «Elements of Statistical Learning Ed. 2», Springer, 2009.

1.11.4. Gradient Tree Boosting

Gradient Tree Boosting o Gradient Boosted Decision Trees (GBDT) es una generalización del boosting a funciones de pérdida diferenciable arbitrarias. GBDT es un procedimiento preciso y efectivo que puede ser usado tanto para problemas de regresión como de clasificación en una variedad de areas, incluyendo la ecología y el ranking de búsquedas Web.

El módulo sklearn.ensemble proporciona métodos para clasificación y regresión mediante árboles de decisión con boosting por gradiente.

Nota

Scikit-learn 0.21 introduce dos nuevas implementaciones y experimentales de árboles con boosting por gradientes, principalmente HistGradientBoostingClassifier y HistGradientBoostingRegressor, inspirado por LightGBM (Ver [LightGBM]).

Estos estimadores basados en histogramas pueden ser órdenes de magnitud más rápidos que GradientBoostingClassifier y GradientBoostingRegressor cuando el número de muestras es mayor que decenas de miles de muestras.

También tienen soporte incorporado para valores faltantes, lo que evita la necesidad de un imputador.

Estos estimadores son descritos con más detalle a continuación en Boosting por gradientes basado en Histogramas.

La siguiente guía se enfoca en GradientBoostingClassifier y GradientBoostingRegressor, lo que podría ser preferido para tamaños pequeños de muestra ya que el binning quizás lleve a puntos de división que son demasiado aproximados con esta configuración.

A continuación se describe el uso y los parámetros de GradientBoostingClassifier y GradientBoostingRegressor. Los 2 parámetros más importantes de estos estimadores son n_estimators y learning_rate.

1.11.4.1. Clasificación

GradientBoostingClassifier soporta tanto clasificación binaria como multiclase. El siguiente ejemplo muestra como ajustar un clasificador de boosting por gradiente con 100 tocones (árboles de un nivel de profundidad) de decisión como aprendices débiles:

>>> from sklearn.datasets import make_hastie_10_2
>>> from sklearn.ensemble import GradientBoostingClassifier

>>> X, y = make_hastie_10_2(random_state=0)
>>> X_train, X_test = X[:2000], X[2000:]
>>> y_train, y_test = y[:2000], y[2000:]

>>> clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0,
...     max_depth=1, random_state=0).fit(X_train, y_train)
>>> clf.score(X_test, y_test)
0.913...

El número de aprendices débiles (por ejemplo, árboles de regresión) es controlado por el parametro n_estimators; El tamaño de cada árbol puede ser controlado tanto estableciendo la profundidad del árbol mediante max_depth o estableciendo el número de nodos de hojas mediante max_leaf_nodes. El learning_rate es ún hiperparámetro en el rango (0.0, 1.0] que controla el sobreajuste mediante el encogimiento .

Nota

La clasificación con más de 2 clases requiere la inducción de n_classes árboles de regresión en cada iteración, por lo que el número total de árboles inducidos es igual a n_clases * n_estimators. Para conjuntos de datos con un número grande de clases recomendamos utilizar HistGradientBoostingClassifier como una alternativa a GradientBoostingClassifier .

1.11.4.2. Regresión

GradientBoostingRegressor soporta un número de diferentes funciones de pérdida para regresión que pueden ser especificadas mediante el argumento loss; la función de pérdida por defecto para la regresión es la de mínimos cuadrados ('ls').

>>> import numpy as np
>>> from sklearn.metrics import mean_squared_error
>>> from sklearn.datasets import make_friedman1
>>> from sklearn.ensemble import GradientBoostingRegressor

>>> X, y = make_friedman1(n_samples=1200, random_state=0, noise=1.0)
>>> X_train, X_test = X[:200], X[200:]
>>> y_train, y_test = y[:200], y[200:]
>>> est = GradientBoostingRegressor(n_estimators=100, learning_rate=0.1,
...     max_depth=1, random_state=0, loss='ls').fit(X_train, y_train)
>>> mean_squared_error(y_test, est.predict(X_test))
5.00...

La siguiente figura muestra los resultados de aplicar GradientBoostingRegressor con pérdida de mínimos cuadrados y 500 aprendices base al conjunto de datos de diabetes (sklearn.datasets.load_diabetes). La gráfica a la izquierda muestra el error de prueba y entrenamiento en cada iteración. El error de entrenamiento en cada iteración se guarda en el atributo train_score_ del modelo de boosting por gradientes. El error de prueba en cada iteración se puede obtener mediante el método staged_predict que devuelve un generador que da las predicciones en cada etapa. Gráficos como estos pueden ser utilizados para determinar el número óptimo de árboles (por ejemplo, n_estimators) por parada anticipada.

Ejemplos:

• Regresión de Potenciación de Gradiente

• Estimados Out-of-Bag de Potenciación de Gradiente

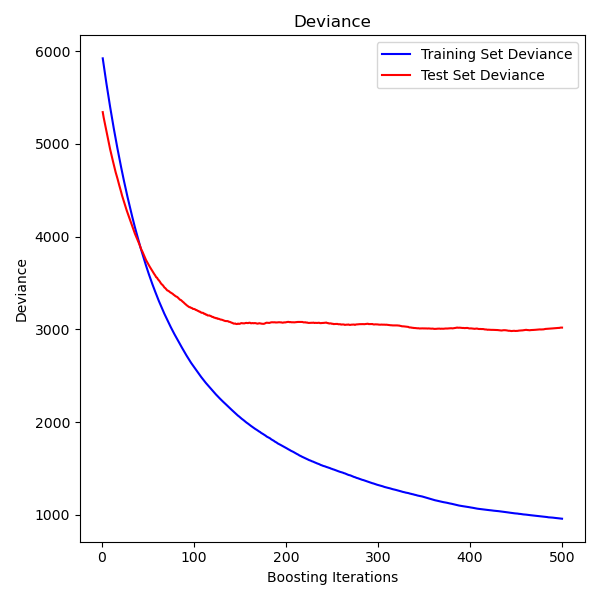
1.11.4.3. Ajustando aprendices débiles adicionales

Tanto GradientBoostingRegressor como GradientBoostingClassifier soportan warm_start=True, el cual te permite añadir mas estimadores a un modelo ya ajustado.

>>> _ = est.set_params(n_estimators=200, warm_start=True)  # set warm_start and new nr of trees
>>> _ = est.fit(X_train, y_train) # fit additional 100 trees to est
>>> mean_squared_error(y_test, est.predict(X_test))
3.84...

1.11.4.4. Controlando el tamaño del árbol

El tamaño de los aprendices del árbol de regresión base define el nivel de interacciones variable que pueden ser capturadas por el modelo de boosting por gradiente. En general, un árbol de profundidad h puede capturar interacciones de orden h. Hay dos formas en la que el tamaño de los árboles de regresión individuales puede ser controlado.

Si tu especificas max_depth=h, entonces se crecerán árboles binarios completos de profundidad h. Tales árboles tendrán (como máximo) 2**h nodos de hoja y 2**h - 1 nodos divididos.

Alternativamente, puedes controlar el tamaño del árbol especificando el número de nodos de hoja mediante el parámetro max_leaf_nodes. En este caso, los árboles crecerán usando una búsqueda best-first donde los nodos con la mayor mejora en la impureza se expandirán primero. Un árbol con max_leaf_nodes=k tiene k - 1 nodos divididos y por lo tanto puede modelar interacciones de hasta el orden max_leaf_nodes=k .

Encontramos que max_leaf_nodes=k da resultados comparables a max_depth=k-1 pero es significativamente mas rapido de entrenar al costo de un error de entrenamiento ligeramente mayor. El parámetro max_leaf_nodes corresponde a la variable J en el capítulo sobre boosting por gradiente en [F2001] y es relacionado al parámetro interaction.depth en el paquete gbm de R donde max_leaf_nodes == interaction.depth +1 .

1.11.4.5. Formulación matemática

Primero presentamos GBRT para la regresión, y luego detallamos el caso por clasificación.

1.11.4.5.1. Regresión

Los regresores GBRT son modelos aditivos cuya predicción \(y_i\) para una entrada dada \(x_i\) es de la siguiente forma:

\[\hat{y_i} = F_M(x_i) = \sum_{m=1}^{M} h_m(x_i)\]

donde los \(h_m\) son estimadores llamados aprendices débiles en el contexto del boosting. Gradient Tree Boosting utiliza regresores de árboles de decisión de tamaño fijo como aprendices débiles. La constante M corresponde al parámetro n_estimators.

Similar a otros algoritmos de boosting, un GBRT se construye de manera codiciosa:

\[F_m(x) = F_{m-1}(x) + h_m(x),\]

donde el árbol recién añadido \(h_m\) es ajustado para minimizar una suma de pérdidas \(L_m\), dado el conjunto anterior \(F_{m-1}\):

\[h_m = \arg\min_{h} L_m = \arg\min_{h} \sum_{i=1}^{n} l(y_i, F_{m-1}(x_i) + h(x_i)),\]

donde \(l(y_i, F(x_i))\) es definido por el parámetro loss, detallado en la siguiente sección.

Por defecto, el modelo inicial :math: F_{0} es elegido como la constante que minimiza la pérdida: para una pérdida de mínimos cuadrados, esta es la media empírica de los valores objetivo. El modelo inicial también puede ser especificado mediante el arugmento ìnit`.

Utilizando una aproximación de Taylor de primer orden, el valor de \(l\) puede aproximarse de la siguiente manera:

\[l(y_i, F_{m-1}(x_i) + h_m(x_i)) \approx l(y_i, F_{m-1}(x_i)) + h_m(x_i) \left[ \frac{\partial l(y_i, F(x_i))}{\partial F(x_i)} \right]_{F=F_{m - 1}}.\]

Nota

En pocas palabras, una aproximación de Taylor de primer orden dice que \(l(z) \approx l(a) + (z - a) \frac{\partial l(a)}{\partial a}\). Aquí, \(z\) corresponde a \(F_{m - 1}(x_i) + h_m(x_i)\), y \(a\) corresponde a \(F_{m-1}(x_i)\)

La cantidad \(\left[ \frac{\partial l(y_i, F(x_i))}{\partial F(x_i)} \right]_{F=F_{m - 1}}\) es la derivada de la pérdida con respecto a su segundo parámetro, evaluado en \(F_{m-1}(x)\). Es fácil calcular por cualquier \(F_{m - 1}(x_i)\) dado en una forma cerrada, ya que la pérdida es diferenciable. Lo denotaremos por \(g_i\).

Eliminando los términos constantes, tenemos:

\[h_m \approx \arg\min_{h} \sum_{i=1}^{n} h(x_i) g_i\]

Esto es minimizado si \(h(x_i)\) es ajustado para predecir un valor que es proporcional al gradiente negativo \(-g_i\). Por lo tanto, en cada iteración, el estimador \(h_m\) es ajustado para predecir los gradientes negativos de las muestras. Los gradientes son actualizados en cada iteración. Esto se puede considerar como alguna especie de descenso por gradiente en un espacio funcional.

Nota

Para algunas pérdidas, por ejemplo, la mínima desviación absoluta (MDA, o LAD en inglés) donde los gradientes son \(\pm 1\), los valores predichos por un \(h_m\) ajustado no son lo suficientemente precisos: el árbol sólo puede generar valores enteros. Como resultado, los valores de las hojas del árbol \(h_m\) se modifican una vez que el árbol es ajustado, de tal forma que los valores de las hojas minimizan la pérdida \(L_m\). Su actualización depende de la pérdida: para la pérdida LAD, el valor de una hoja se actualiza a la mediana de las muestras en esa hoja.

1.11.4.5.2. Clasificación

El boosting por gradiente para la clasificación es muy similar al caso de regresión. Sin embargo, la suma de los árboles \(F_M(x_i) = \sum_m h_m(x_i)\) no es homogénea a una predicción: no puede ser una clase, ya que los árboles predicen valores continuos.

El mapeo desde el valor \(F_M(x_i)\) a una clase o una probabilidad es dependiente de pérdidas. Para la desviación (o log-loss, es decir, perdida de logistica), la probabilidad de que \(x_i\) pertenezca a la clase positiva está modelada como \(p(y_i = 1 | x_i) = \sigma(F_M(x_i)\) donde \(\sigma\) es la función sigmoid.

Para la clasificación multiclase, los árboles K (para clases K) se construyen en cada una de las iteraciones \(M\). La probabilidad de que \(x_i\) pertenezca a la clase k se modela como un softmax de los valores \(F_{M,k}(x_i)\).

Tenga en cuenta que incluso para una tarea de clasificación, el sub-estimador \(h_m\) sigue siendo un regresor, no un clasificador. Esto es debido a que los sub-estimadores estan entrenados para predecir gradientes (negativos), los cuales siempre son cantidades continuas.

1.11.4.6. Funciones de pérdida

Las siguientes funciones de pérdida son soportadas y se pueden especificar usando el parámetro loss:

• Regresión

  • Mínimos cuadrados ('ls'): La elección natural para la regresión debido a sus propiedades computacionales superiores. El modelo inicial es dado por la media de los valores objetivo.

  • Menor desviación absoluta ('lad'): Una función de pérdida robusta para la regresión. El modelo inicial es dado por la mediana de los valores objetivo.

  • Huber ('huber'): Otra función de pérdida robusta que combina mínimos cuadrados y menor desviación absoluta; utilice alpha para controlar la sensibilidad con respecto a los valores atípicos (ver [F2001] para más detalles).

  • Quantile ('quantile'): Una función de pérdida para regresión de cuantiles. Utilice 0 < alfa < 1 para especificar el cuantil. Esta función de pérdida puede utilizarse para crear intervalos de predicción (ver Intervalos de predicción para la Regresión con Potenciación de Gradiente).

• Clasificación

  • Desviación binomial ('deviance'): La función de pérdida del logaritmo de la verosimilitud binomial negativa para la clasificación binaria (provee estimaciones de probabilidad). El modelo inicial viene dado por el logaritmo de la razón de probabilidades.

  • Desviación multinomial ('deviance'): La función de pérdida del logaritmo de la verosimilitud multinomial negativa para clasificación multiclase con n_classes clases mutuamente exclusivas. Proporciona estimaciones de probabilidad. El modelo inicial está dado por la probabilidad a priori de cada clase. En cada iteración n_classes los árboles de regresión deben ser construidos, lo que hace que GBRT sea algo ineficiente para conjuntos de datos con un gran número de clases.

  • Pérdida exponencial ('exponential'): La misma función de perdida que AdaBoostClassifier. Menos robusta para los ejemplos mal etiquetados que 'deviance', solo puede ser usada para la clasificación binaria.

1.11.4.7. Reducción a través de la tasa de aprendizaje

[F2001] propuso una sencilla estrategia de regularización que escala la contribución de cada aprendiz débil por un factor constante \(\nu\):

\[F_m(x) = F_{m-1}(x) + \nu h_m(x)\]

El parámetro \(\nu\) es también llamado la tasa de aprendizaje porque escala la longitud de paso del procedimiento de descenso de gradiente; se puede establecer a través del parámetro learning_rate.

El parámetro learning_rate interactúa fuertemente con el parámetro n_estimators, el número de algoritmos de aprendizaje débiles a ajustar. Valores mas pequeños de learning_rate requieren de grandes números de algoritmos de aprendizaje débiles para mantener un error de entrenamiento constante. La evidencia empírica sugiere que valores pequeños de learning_rate favorecen un mejor error de pruebas. [HTF] recomiendan establecer la tasa de aprendizaje en una constante pequeña (por ejemplo, learning_rate <= 0.1), y escoger n_estimators mediante una parada anticipada. Para una discusión mas detallada de la interacción entre learning_rate y n_estimators consulta [R2007].

1.11.4.8. Submuestreo

[F1999] propone boosting por gradiente estocástico, lo cual combina el boosting por gradiente con el promediado de bootstrap (bagging). En cada iteración el clasificador base es entrenado en una fracción subsamples de los datos de entrenamiento disponibles. La submuestra es escogida sin reemplazo. Un valor típico de subsamples es 0.5.

La figura a continuación ilustra el efecto de la reducción y el submuestreo sobre la calidad del ajuste del modelo. Podemos ver claramente que el rendimiento es mayor con reducción que sín reducción. El submuestreo con reducción puede aumentar aún mas la precisión del modelo. Sin embargo, el submuestreo sín reducción tiene un resultado pobre.

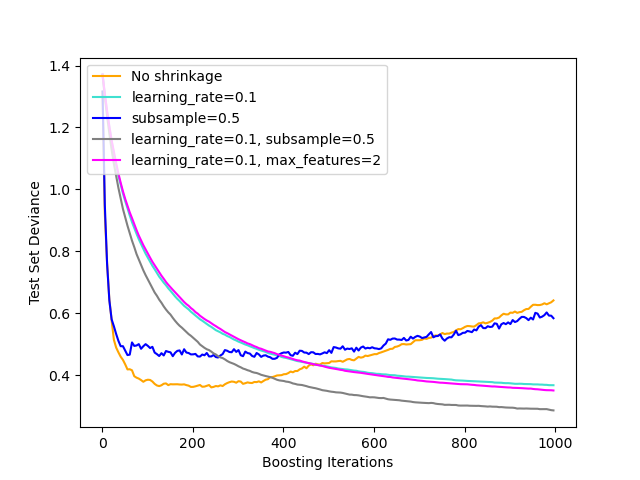
Otra estrategia para reducir la varianza es mediante el submuestreo de las características análogas a las divisiones aleatorias en RandomForestClassifier . El número de características submuestreadas puede ser controlado mediante el parámetro max_features.

Nota

Usar un valor max_features pequeño puede reducir significativamente el tiempo de ejecución.

El boosting por gradiente stocástico permite la computación de estimados fuera-de-bolsa de la desviación prueba mediante el calculo de la mejore en desviación de los ejemplos que no son incluidos en la muestra de bootstrap (es decir, los ejemplos fuera-de-bolsa). Las mejoras son almacenadas en el atributo oob_improvement_. oob_improvement_[i] guarda la mejora en terminos de la pérdida en las muestras fuera-de-bolsa (OOB) si añades la i-ésima etapa a las predicciones actuales. Los estimados fuera-de-bolsa pueden ser utilizados para la selección de modelos, por ejemplo, para determinar el número de iteraciones original. Los estimados OOB suelen ser bastante pesimistas, por lo que recomendamos recurrir a ella solamente si la validación cruzada utiliza demasiado tiempo.

Ejemplos:

• Regularización del Potenciador de Gradiente (Gradient Boosting)

• Estimados Out-of-Bag de Potenciación de Gradiente

• Errores OOB para bosques aleatorios (random forests)

1.11.4.9. Interpretación con importancia de característica

Los árboles de decisión individuales se pueden interpretar fácilmente si se visualiza la estructura del árbol. Los modelos de boosting por gradiente, sin embargo, comprenden cientos de árboles de regresión, por lo que no pueden ser fácilmente interpretados por inspección visual de los árboles individuales. Afortunadamente, una diversidad de técnicas han sido propuestas para resumir e interpretar modelos de boosting por gradiente.

A menudo las características no contribuyen de manera equitativa para predecir la respuesta objetivo; en muchas situaciones la mayoría de las características, son de hecho irrelevantes. Cuando se interpreta un modelo, la primera pregunta suele ser: ¿cuáles son estas características importantes? y ¿cómo contribuyen a predecir la respuesta objetivo?

Los árboles de decisión individuales realizan de manera intrínseca una selección de características al elegir puntos de división apropiados. Esta información puede ser utilizada para medir la importancia de cada característica; la idea fundamental es: mientras mas seguido se utilice una característica en los puntos de división de un árbol mas importante sera esta característica. Esta noción de importancia puede ser extendida a los conjuntos de árboles de decisión si simplemente se promedia la importancia de característica basadas en la impureza de cada árbol (see Evaluación de importancia de características for more details).

Los puntajes de importancia de característica de un modelo de boosting por gradientes ya ajustado puede ser accedido mediante la propiedad feature_importances_:

>>> from sklearn.datasets import make_hastie_10_2
>>> from sklearn.ensemble import GradientBoostingClassifier

>>> X, y = make_hastie_10_2(random_state=0)
>>> clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0,
...     max_depth=1, random_state=0).fit(X, y)
>>> clf.feature_importances_
array([0.10..., 0.10..., 0.11..., ...

Ten en cuenta que este cálculo de la importancia de características está basado en la entropía, y es distinto a sklearn.inspection.permutation_importance el cual está basado en la permutación de las características.

Ejemplos:

• Regresión de Potenciación de Gradiente

1.11.5. Boosting por gradientes basado en Histogramas

Scikit-learn 0.21 introduce dos nuevas implementaciones experimentales de árboles de boosting por gradientes, HistGradientBoostingClassifier y HistGradientBoostingRegressor, inspirado por LightGBM (Ver [LightGBM]).

Estos estimadores basados en histogramas pueden ser órdenes de magnitud más rápidos que GradientBoostingClassifier y GradientBoostingRegressor cuando el número de muestras es mayor que decenas de miles de muestras.

También tienen soporte incorporado para valores faltantes, lo que evita la necesidad de un imputador.

Estos estimadores rápidos primero recolectan las muestras de entrada X en intervalos de valores enteros (usualmente 256 intervalos) lo cual reduce tremendamente el número de puntos de división a considerar, y permite al algoritmo aprovechar estructuras de datos basadas en enteros (histogramas) en lugar de confiar en valores continuos ordenados cuando se construyen los árboles. La API de estos estimadores es ligeramente distinto, y algunas de las funciones de GradientBoostingClassifier y GradientBoostingRegressor aún no son soportadas, por ejemplo algunas funciones de pérdida.

Estos estimadores aún son experimentales: sus predicciones y su API quizás tengan que cambiar sin ningún ciclo de obsolescencia. Para utilizarlas, tienes que importar de manera explicita enable_hist_gradient_boosting:

>>> # explicitly require this experimental feature
>>> from sklearn.experimental import enable_hist_gradient_boosting  # noqa
>>> # now you can import normally from ensemble
>>> from sklearn.ensemble import HistGradientBoostingClassifier

Ejemplos:

• Gráficos de Dependencia Parcial y de Expectativa Condicional Individual

1.11.5.1. Uso

La mayoría de los parámetros no cambian de GradientBoostingClassifier y GradientBoostingRegressor. Una excepción es el parámetro max_iter que sustituye a n_estimators, y controla el número de iteraciones del proceso de boosting:

>>> from sklearn.experimental import enable_hist_gradient_boosting
>>> from sklearn.ensemble import HistGradientBoostingClassifier
>>> from sklearn.datasets import make_hastie_10_2

>>> X, y = make_hastie_10_2(random_state=0)
>>> X_train, X_test = X[:2000], X[2000:]
>>> y_train, y_test = y[:2000], y[2000:]

>>> clf = HistGradientBoostingClassifier(max_iter=100).fit(X_train, y_train)
>>> clf.score(X_test, y_test)
0.8965

Las pérdidas disponibles para la regresión son “least_squares”, “least_absolute_deviation”, que es menos sensible a los valores atípicos, y “poisson”, que se adapta bien a las cuentas de modelos y frecuencias. Para la clasificación, “binary_crossentropy” se utiliza para la clasificación binaria y “categorical_crossentropy” se utiliza para la clasificación multiclase. Por defecto, la pérdida es “auto” y seleccionará la pérdida apropiada dependiendo de y pasado a fit.

El tamaño de los árboles puede controlarse a través de los parámetros max_leaf_nodes, max_depth, y min_samples_leaf.

El número de contenedores usados para recolectar los datos se controla con el parámetro max_bins. Usar menos contenedores actúa como una forma de regularización. Generalmente se recomienda utilizar el mayor número posible de contenedores, el cual es el valor predeterminado.

El parámetro l2_regularization es un regularizador en la función de pérdida y corresponde a \(\lambda\) en la ecuación (2) de [XGBoost].

Ten en cuenta que el parado temprano esta habilitado por defecto si el número de muestras es mayor que 10,000. El comportamiento del parado temprano es controlado mediante los parámetros validation_fraction, n_iter_no_change, y tol. Es posible parar temprano usando un scorer arbitrario, o simplemente la perdida de entrenamiento o validación. Sin embargo, por razones técnicas, usar un scorer es significativamente mas lento que utilizar la perdida. Por defecto, se utiliza el parado temprano si hay por lo menos 10,000 muestras en el conjunto de entrenamiento, utilizando la pérdida por validación.

1.11.5.2. Soporte para valores faltantes

HistGradientBoostingClassifier y HistGradientBoostingRegressor tienen soporte integrado para valores faltantes (NaNs).

Durante el entrenamiento, el cultivador de árboles aprende en cada punto de división si las muestras con valores faltantes deberían ir al hijo de la izquierda o la derecha, basado en la ganancia potencial. Cuando se realiza la predicción, las muestras con valores faltantes son asignadas consecuentemente al hijo de la izquierda o la derecha:

>>> from sklearn.experimental import enable_hist_gradient_boosting  # noqa
>>> from sklearn.ensemble import HistGradientBoostingClassifier
>>> import numpy as np

>>> X = np.array([0, 1, 2, np.nan]).reshape(-1, 1)
>>> y = [0, 0, 1, 1]

>>> gbdt = HistGradientBoostingClassifier(min_samples_leaf=1).fit(X, y)
>>> gbdt.predict(X)
array([0, 0, 1, 1])

Cuando el patrón de falta es predictivo, las divisiones pueden ser realizadas dependiendo sí falta el valor de característica o no:

>>> X = np.array([0, np.nan, 1, 2, np.nan]).reshape(-1, 1)
>>> y = [0, 1, 0, 0, 1]
>>> gbdt = HistGradientBoostingClassifier(min_samples_leaf=1,
...                                       max_depth=2,
...                                       learning_rate=1,
...                                       max_iter=1).fit(X, y)
>>> gbdt.predict(X)
array([0, 1, 0, 0, 1])

Si no se encontraron valores faltantes para una característica determinada durante el entrenamiento, entonces las muestras con valores faltantes se mapean al hijo que tenga más muestras.

1.11.5.3. Soporte para ponderado de muestras

HistGradientBoostingClassifier y HistGradientBoostingRegressor soportan ponderados durante fit.

El siguiente ejemplo de juguete demuestra cómo el modelo ignora las muestras con cero ponderado de muestra:

>>> X = [[1, 0],
...      [1, 0],
...      [1, 0],
...      [0, 1]]
>>> y = [0, 0, 1, 0]
>>> # ignore the first 2 training samples by setting their weight to 0
>>> sample_weight = [0, 0, 1, 1]
>>> gb = HistGradientBoostingClassifier(min_samples_leaf=1)
>>> gb.fit(X, y, sample_weight=sample_weight)
HistGradientBoostingClassifier(...)
>>> gb.predict([[1, 0]])
array([1])
>>> gb.predict_proba([[1, 0]])[0, 1]
0.99...

Como puedes ver, el [1, 0] se clasifica cómodamente como 1 ya que las dos primeras muestras son ignoradas debido a sus ponderados de muestra.

Detalle de la implementación: tomar en cuenta los ponderados de las muestras equivale a multiplicar los gradientes (y los hessians) por los ponderados de las muestras. Note que la etapa de binning (específicamente el cálculo de cuantías) no toma en cuenta los ponderados.

1.11.5.4. Soporte de características categóricas

HistGradientBoostingClassifier y HistGradientBoostingRegressor tienen soporte nativo para características categóricas: las dos pueden considerar divisiones en datos categóricos no ordenados.

Para conjuntos de datos con características categóricas, usar el soporte nativo categórico suele ser mejor que depender de la codificación one-hot (OneHotEncoder), ya que la codificación one-hot requiere más profundidad del árbol para obtener divisiones equivalentes. También generalmente es mejor depender en el soporte categórico nativo que tomar las características categóricas como continuas (ordinal), lo cual ocurre para datos categóricos codificados en ordinal, ya que las categorías son cantidades nominales donde el orden no importa.

Para activar el soporte categórico, se puede pasar una máscara booleana al parámetro categorical_features, indicando qué característica es categórica. En lo siguiente, la primera característica será tomada como categórica y la segunda característica como numérica:

>>> gbdt = HistGradientBoostingClassifier(categorical_features=[True, False])

Equivalentemente, uno puede pasar una lista de enteros indicando los índices de las características categóricas:

>>> gbdt = HistGradientBoostingClassifier(categorical_features=[0])

La cardinalidad de cada característica categórica debe ser menor que el parámetro max_bins, y se espera que cada característica categórica este codificada en [0, max_bins - 1]. Para este fin, quizás sea útil pre-procesar los datos con un OrdinalEncoder como se hace en Soporte de características categóricas en Potenciación del Gradiente (Gradient Boosting).

Si hay valores faltantes durante el entrenamiento, estos serán tratados como una categoría adecuada. Si no hay valores faltantes durante el entrenamiento, entonces en el tiempo de predicción, los valores faltantes son mapeados al nodo hijo que tenga el mayor número de muestras (igual que en la características continuas). Durante la predicción, las categorías que no fueron vistas durante el tiempo de ajuste serán tratadas como valores faltantes.

Búsqueda de divisiones con características categóricas: La manera canónica de considerar divisiones categóricas en un árbol es considerar todas las particiones \(2^{K - 1} - 1\), donde \(K\) es el número de categorías. Esto puede volverse prohibitivo rápidamente si \(K\) es grande. Afortunadamente, ya que los árboles de potenciación de gradiente son siempre árboles de regresión (incluso para problemas de clasificación), existe una estrategia más rápida que puede dar divisiones equivalentes. Primero, las categorías de una característica son ordenadas de acuerdo a la varianza del objetivo, por cada categoría k. Después de que las categorías sean ordenadas, uno puede considerar particiones continuas, es decir, tratar las categorías como si fueran valores continuos ordenados (ver Fisher [Fisher1958] para una prueba formal). Como resultado, solo \(K - 1\) divisiones deben ser consideradas en lugar de \(2^{K - 1} - 1\). El sorteo inicial es una operación \(\mathcal{O}(K \log(K))\), lo cual lleva a una complejidad total de \(\mathcal{O}(K \log(K) + K)\), en lugar de \(\mathcal{O}(2^K)\).

Ejemplos:

• Soporte de características categóricas en Potenciación del Gradiente (Gradient Boosting)

1.11.5.5. Restricciones monotónicas

Dependiendo del problema en cuestión, quizás tengas conocimientos previos indicando que una característica particular debería tener, por lo general, un efecto positivo (o negativo) en el valor objetivo. Por ejemplo, si todo lo demás es igual, una mayor calificación de solvencia debería incrementar la probabilidad de que se apruebe un préstamo. Las restricciones monotónicas te permiten incorporar estos conocimientos previos dentro del modelo.

Una restricción monotónica positiva es una restricción de la forma:

\(x_1 \leq x_1' \implies F(x_1, x_2) \leq F(x_1', x_2)\), donde \(F\) es el predictor con dos características.

De la misma manera, una restricción monotónica negativa es de la forma:

\(x_1 \leq x_1' \\implies F(x_1, x_2) \\geq F(x_1', x_2)\).

Tenga en cuenta que las restricciones monotónicas solo restringen la salida «todo lo demás siendo igual». En efecto, la siguiente relación no es forzada por una restricción positiva: \(x_1 \leq x_1' \implies F(x_1, x_2) \leq F(x_1', x_2')\).

Puedes especificar una restricción monotónica en cada característica usando el parámetro monotonic_cst. Para cada característica, un valor de 0 indica que no hay ninguna restricción, mientras que -1 y 1 indica una restricción negativa y positiva, respectivamente:

>>> from sklearn.experimental import enable_hist_gradient_boosting  # noqa
>>> from sklearn.ensemble import HistGradientBoostingRegressor

... # positive, negative, and no constraint on the 3 features
>>> gbdt = HistGradientBoostingRegressor(monotonic_cst=[1, -1, 0])

En el contexto de una clasificación binaria, imponer una restricción monotónica significa que la característica debe tener un efecto positivo / negativo en la probabilidad de pertenecer a la clase positiva. Las restricciones monotónicas no están soportadas en un contexto multiclase.

Nota

Ya que las categorías son cantidades no ordenadas, no es posible imponer restricciones monotónicas sobre características categóricas.

Ejemplos:

• Restricciones monotónicas

1.11.5.6. Paralelismo de bajo nivel

HistGradientBoostingClassifier y HistGradientBoostingRegressor tienen implementaciones que usan OpenMP para la paralelización a través de Cython. Para más detalles sobre cómo controlar el número de hilos, por favor consulte nuestras notas de Paralelismo.

Las siguientes partes son paralelizadas:

• el mapeado de muestras desde valores reales a contenedores de valores enteros (sin embargo, encontrar los umbrales de los contenedores es secuencial)

• la construcción de histogramas está paralelizada sobre características

• la búsqueda del mejor punto de división en un nodo es paralelizado sobre características

• durante el ajuste, el mapeo de muestras a los hijos de izquierda y derecha es paralelizado sobre muestras

• los cálculos de gradiente y hessians son paralelizados sobre muestras

• la predicción es paralelizada sobre muestras

1.11.5.7. Porqué es más rápido

El cuello de botella de un procedimiento de boosting por gradientes es la construcción de los árboles de decisión. Construir un árbol de decisión tradicional (como en los otros GBDT, GradientBoostingClassifier and GradientBoostingRegressor) requiere ordenar las muestras en cada nodo (por cada característica). Es necesario ordenar para que cada aumento potencial de un punto de división pueda ser calculado eficientemente. Dividir un único nodo tiene entonces una complejidad de \(\mathcal{O}(n_\text{features} \times n \log(n))\) donde \(n\) es el número de muestras en el nodo.

HistGradientBoostingClassifier y HistGradientBoostingRegressor, en contraste, no requieren ordenar los valores de las características y en su lugar usar una estructura de datos llamada histograma, donde las muestras están ordenadas implícitamente. Construir un histograma tiene una complejidad \(\mathcal{O}(n)\), así que el procedimiento de división del nodo tiene una complejidad de \(\mathcal{O}(n_\text{features} \times n)\), mucho más pequeño que el anterior. Además, en lugar de considerar \(n\) puntos divididos, aquí consideramos sólo max_bins puntos de división, que es mucho más pequeño.

Para construir histogramas, los datos de entrada X necesitan ser recolectados en contenedores de valores enteros. Este procedimiento de binning si requiere ordenar los valores de característica, pero sólo ocurre una vez al principio del proceso de boosting (no en cada nodo, como en GradientBoostingClassifier y GradientBoostingRegressor).

Finalmente, muchas partes de la implementación de HistGradientBoostingClassifier y HistGradientBoostingRegressor son paralelizadas.

Referencias

F1999

Friedmann, Jerome H., 2007, «Stochastic Gradient Boosting»

R2007

G. Ridgeway, «Generalized Boosted Models: A guide to the gbm package», 2007

XGBoost

Tianqi Chen, Carlos Guestrin, «XGBoost: A Scalable Tree Boosting System»

LightGBM(1,2)

Ke et. al. «LightGBM: A Highly Efficient Gradient BoostingDecision Tree»

Fisher1958

Walter D. Fisher. «On Grouping for Maximum Homogeneity»

1.11.6. Clasificador de voto

La idea detrás de VotingClassifier es combinar clasificadores de aprendizaje automático conceptualmente diferentes y usar un voto por mayoría o el promedio de probabilidades predichas (voto blando) para predecir las etiquetas de clase. Este tipo de clasificador puede ser útil para un conjunto de modelos de igual rendimiento a fin de equilibrar sus debilidades individuales.

1.11.6.1. Etiquetas de clase mayoritarias (mayoría/voto duro)

En la votación por mayoría, la etiqueta de clase predicha para una muestra en particular es aquella etiqueta de clase que representa la mayoría (modo) de las etiquetas de clases predichas por cada clasificador individual.

Por ejemplo, si la predicción de una muestra dada es

• clasificador 1 -> clase 1

• clasificador 2 -> clase 1

• clasificador 3 -> clase 2

el VotingClassifier (con voting='hard') clasificaría la muestra como «clase 1» basada en la etiqueta de clase mayoritaria.

En el caso de un empate, el VotingClassifier seleccionará la clase basada en el orden de clasificación ascendente. Por ejemplo, en el siguiente escenario

• clasificador 1 -> clase 2

• clasificador 2 -> clase 1

la etiqueta de clase 1 será asignada a la muestra.

1.11.6.2. Uso

El siguiente ejemplo muestra cómo ajustar el clasificador por regla de mayoría:

>>> from sklearn import datasets
>>> from sklearn.model_selection import cross_val_score
>>> from sklearn.linear_model import LogisticRegression
>>> from sklearn.naive_bayes import GaussianNB
>>> from sklearn.ensemble import RandomForestClassifier
>>> from sklearn.ensemble import VotingClassifier

>>> iris = datasets.load_iris()
>>> X, y = iris.data[:, 1:3], iris.target

>>> clf1 = LogisticRegression(random_state=1)
>>> clf2 = RandomForestClassifier(n_estimators=50, random_state=1)
>>> clf3 = GaussianNB()

>>> eclf = VotingClassifier(
...     estimators=[('lr', clf1), ('rf', clf2), ('gnb', clf3)],
...     voting='hard')

>>> for clf, label in zip([clf1, clf2, clf3, eclf], ['Logistic Regression', 'Random Forest', 'naive Bayes', 'Ensemble']):
...     scores = cross_val_score(clf, X, y, scoring='accuracy', cv=5)
...     print("Accuracy: %0.2f (+/- %0.2f) [%s]" % (scores.mean(), scores.std(), label))
Accuracy: 0.95 (+/- 0.04) [Logistic Regression]
Accuracy: 0.94 (+/- 0.04) [Random Forest]
Accuracy: 0.91 (+/- 0.04) [naive Bayes]
Accuracy: 0.95 (+/- 0.04) [Ensemble]

1.11.6.3. Promedio ponderado de probabilidades (Votación blanda)

En contraste con la votación por mayoría (votación dura), el voto blando devuelve la etiqueta de clase como argmax de la suma de probabilidades predichas.

Se pueden asignar ponderados específicos a cada clasificador mediante el parámetro weights. Cuando se proporcionan ponderados, las probabilidades de clase para cada clasificador son recolectadas, multiplicadas por el ponderado del clasificador, y promediadas. La etiqueta de clase final se deriva entonces de la etiqueta de clase con la probabilidad media más alta.

Para ilustrar esto con un ejemplo sencillo, supongamos que tengamos 3 clasificadores y un problema de clasificación de 3 clases donde asignamos ponderados iguales a todos los clasificadores: w1=1, w2=1, w3=1.

Las probabilidades medias ponderadas para una muestra entonces se calcularían de la siguiente forma:

clasificador	clase 1	clase 2	clase 3
clasificador 1	w1 * 0.2	w1 * 0.5	w1 * 0.3
clasificador 2	w2 * 0.6	w2 * 0.3	w2 * 0.1
clasificador 3	w3 * 0.3	w3 * 0.4	w3 * 0.3
promedio ponderado	0.37	0.4	0.23

Aquí, la etiqueta de clase predicha es 2, ya que tiene la probabilidad media más alta.

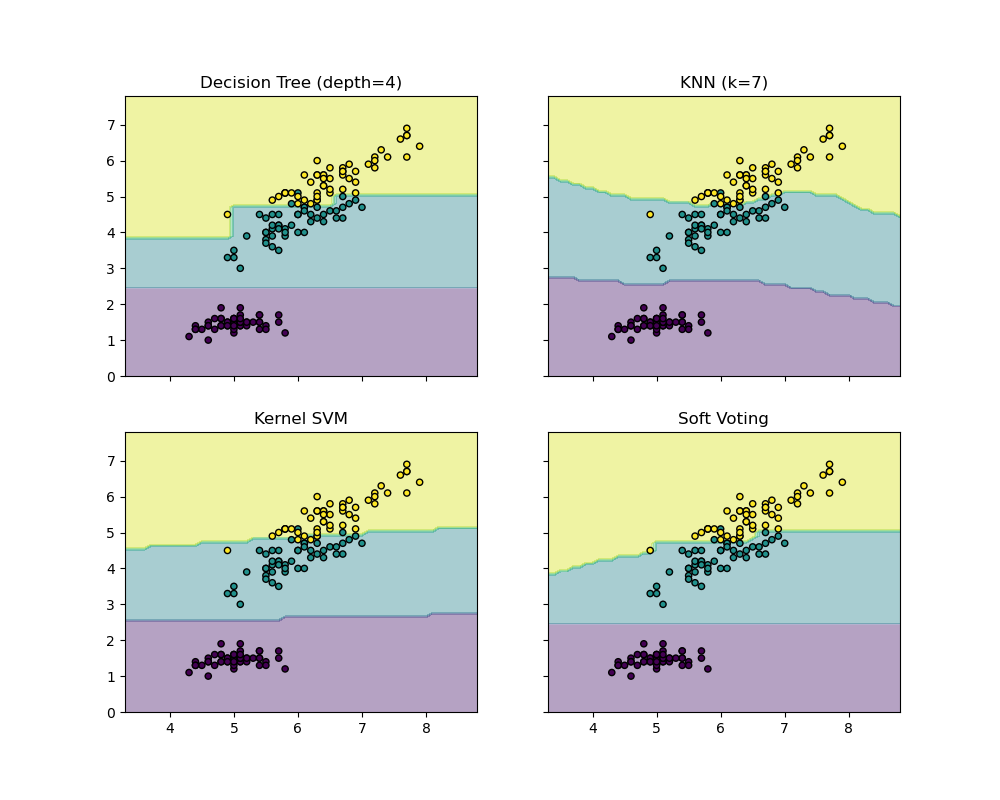
El siguiente ejemplo ilustra como las regiones de decisión quizás cambien cuando un VotingClassifier blando se utilice basado en una maquína de vectores de apoyo lineal, un árbol de decisiones y un clasificador de vecinos K-nearest:

>>> from sklearn import datasets
>>> from sklearn.tree import DecisionTreeClassifier
>>> from sklearn.neighbors import KNeighborsClassifier
>>> from sklearn.svm import SVC
>>> from itertools import product
>>> from sklearn.ensemble import VotingClassifier

>>> # Loading some example data
>>> iris = datasets.load_iris()
>>> X = iris.data[:, [0, 2]]
>>> y = iris.target

>>> # Training classifiers
>>> clf1 = DecisionTreeClassifier(max_depth=4)
>>> clf2 = KNeighborsClassifier(n_neighbors=7)
>>> clf3 = SVC(kernel='rbf', probability=True)
>>> eclf = VotingClassifier(estimators=[('dt', clf1), ('knn', clf2), ('svc', clf3)],
...                         voting='soft', weights=[2, 1, 2])

>>> clf1 = clf1.fit(X, y)
>>> clf2 = clf2.fit(X, y)
>>> clf3 = clf3.fit(X, y)
>>> eclf = eclf.fit(X, y)

1.11.6.4. Usando el VotingClassifier con GridSearchCV

El VotingClassifier también puede ser usado junto con GridSearchCV para afinar los hiperparámetros de los estimadores individuales:

>>> from sklearn.model_selection import GridSearchCV
>>> clf1 = LogisticRegression(random_state=1)
>>> clf2 = RandomForestClassifier(random_state=1)
>>> clf3 = GaussianNB()
>>> eclf = VotingClassifier(
...     estimators=[('lr', clf1), ('rf', clf2), ('gnb', clf3)],
...     voting='soft'
... )

>>> params = {'lr__C': [1.0, 100.0], 'rf__n_estimators': [20, 200]}

>>> grid = GridSearchCV(estimator=eclf, param_grid=params, cv=5)
>>> grid = grid.fit(iris.data, iris.target)

1.11.6.5. Uso

Para predecir las etiquetas de clase basadas en las probabilidades de clase predichas (los estimadores de scikit-learn en el VotingClassifier deben soportar el método predict_proba):

>>> eclf = VotingClassifier(
...     estimators=[('lr', clf1), ('rf', clf2), ('gnb', clf3)],
...     voting='soft'
... )

Opcionalmente, se pueden proporcionar ponderados para clasificadores individuales:

>>> eclf = VotingClassifier(
...     estimators=[('lr', clf1), ('rf', clf2), ('gnb', clf3)],
...     voting='soft', weights=[2,5,1]
... )

1.11.7. Regresor de voto

La idea detrás del VotingClassifier es combinar regresores de aprendizaje automático conceptualmente distintos y devolver los valores promedio predichos. Este tipo de regresor puede ser útil para un conjunto de modelos de igual rendimiento a fin de equilibrar sus debilidades individuales.

1.11.7.1. Uso

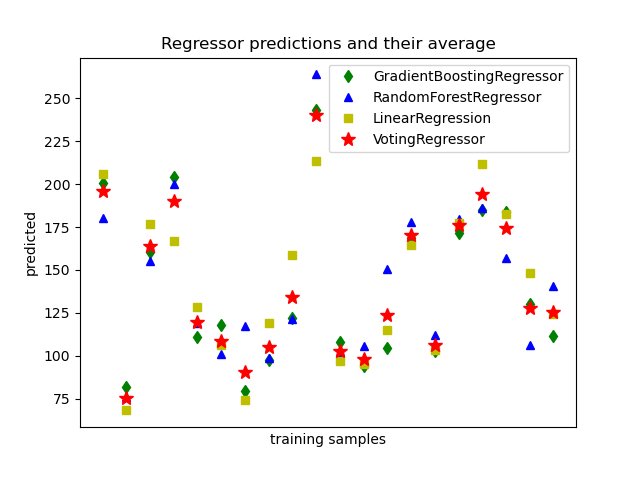
El siguiente ejemplo muestra cómo ajustar el VotingRegressor:

>>> from sklearn.datasets import load_diabetes
>>> from sklearn.ensemble import GradientBoostingRegressor
>>> from sklearn.ensemble import RandomForestRegressor
>>> from sklearn.linear_model import LinearRegression
>>> from sklearn.ensemble import VotingRegressor

>>> # Loading some example data
>>> X, y = load_diabetes(return_X_y=True)

>>> # Training classifiers
>>> reg1 = GradientBoostingRegressor(random_state=1)
>>> reg2 = RandomForestRegressor(random_state=1)
>>> reg3 = LinearRegression()
>>> ereg = VotingRegressor(estimators=[('gb', reg1), ('rf', reg2), ('lr', reg3)])
>>> ereg = ereg.fit(X, y)

Ejemplos:

• Graficar las predicciones de la regresión individual y de la votación

1.11.8. Generalización apilada

La generalización apilada es un método combinar estimadores y así reducir sus sesgos [W1992] [HTF]. Para ser mas precisos, las predicciones de cada estimador individual se apilan juntos y se usan como entrada a un estimador final para calcular la predicción. Este ultimo estimador es entrenado a través de la validación cruzada.

Los StackingClassifier y StackingRegressor proporcionan tales estrategias, las cuales se pueden aplicar a problemas tanto de clasificación como de regresión.

El parámetro estimators corresponde a la lista de estimadores que se apilan juntos en paralelo en los datos de entrada. Debe ser dado como una lista de nombres y estimadores:

>>> from sklearn.linear_model import RidgeCV, LassoCV
>>> from sklearn.neighbors import KNeighborsRegressor
>>> estimators = [('ridge', RidgeCV()),
...               ('lasso', LassoCV(random_state=42)),
...               ('knr', KNeighborsRegressor(n_neighbors=20,
...                                           metric='euclidean'))]

El final_estimator usará las predicciones de los estimators como entrada. Debe ser un clasificador o un regresor cuando se utiliza StackingClassifier o StackingRegressor, respectivamente:

>>> from sklearn.ensemble import GradientBoostingRegressor
>>> from sklearn.ensemble import StackingRegressor
>>> final_estimator = GradientBoostingRegressor(
...     n_estimators=25, subsample=0.5, min_samples_leaf=25, max_features=1,
...     random_state=42)
>>> reg = StackingRegressor(
...     estimators=estimators,
...     final_estimator=final_estimator)

Para entrenar a estimators y final_estimator, el método fit necesita ser llamado en los datos de entrenamiento:

>>> from sklearn.datasets import load_diabetes
>>> X, y = load_diabetes(return_X_y=True)
>>> from sklearn.model_selection import train_test_split
>>> X_train, X_test, y_train, y_test = train_test_split(X, y,
...                                                     random_state=42)
>>> reg.fit(X_train, y_train)
StackingRegressor(...)

Durante el entrenamiento, los estimators se ajustan en todos los datos de entrenamiento X_train. Serán utilizados al llamar a predict o predict_proba. Para generalizar y evitar sobreajustes, el final_estimator es entrenado en muestras externas usando sklearn.model_selection.cross_val_predict internamente.

Para StackingClassifier, tenga en cuenta que la salida de los estimators está controlada por el parámetro stack_method y es llamada por cada estimador. Este parámetro puede ser tanto una cadena, con los nombres de métodos de estimador, o 'auto' que identificará automáticamente un método disponible dependiendo de la disponibilidad, probado en el siguiente orden de preferencia: predict_proba, decision_function y predict.

Un StackingRegressor y un StackingClassifier pueden ser usados como cualquier otro regresor o clasificador, exponiendo los métodos predict, predict_proba, y decision_function, por ejemplo.:

>>> y_pred = reg.predict(X_test)
>>> from sklearn.metrics import r2_score
>>> print('R2 score: {:.2f}'.format(r2_score(y_test, y_pred)))
R2 score: 0.53

Ten en cuenta que también es posible obtener la salida de los estimators apilados utilizando el método transform:

>>> reg.transform(X_test[:5])
array([[142..., 138..., 146...],
       [179..., 182..., 151...],
       [139..., 132..., 158...],
       [286..., 292..., 225...],
       [126..., 124..., 164...]])

En la práctica, un predictor de apilado predice tan bien como el mejor predictor de la capa base e inclusive a veces lo supera combinando las diferentes fortalezas de estos predictores. Sin embargo, entrenar un predictor apilado es costoso computacionalmente.

Nota

Para StackingClassifier, al usar stack_method_='predict_proba', la primera columna se elimina cuando el problema es un problema de clasificación binaria. En efecto, ambas columnas de probabilidad predichas por cada estimador son perfectamente colineales.

Nota

Múltiples capas de apilación se pueden conseguir asignando final_estimator a un StackingClassifier o StackingRegressor:

>>> final_layer_rfr = RandomForestRegressor(
...     n_estimators=10, max_features=1, max_leaf_nodes=5,random_state=42)
>>> final_layer_gbr = GradientBoostingRegressor(
...     n_estimators=10, max_features=1, max_leaf_nodes=5,random_state=42)
>>> final_layer = StackingRegressor(
...     estimators=[('rf', final_layer_rfr),
...                 ('gbrt', final_layer_gbr)],
...     final_estimator=RidgeCV()
...     )
>>> multi_layer_regressor = StackingRegressor(
...     estimators=[('ridge', RidgeCV()),
...                 ('lasso', LassoCV(random_state=42)),
...                 ('knr', KNeighborsRegressor(n_neighbors=20,
...                                             metric='euclidean'))],
...     final_estimator=final_layer
... )
>>> multi_layer_regressor.fit(X_train, y_train)
StackingRegressor(...)
>>> print('R2 score: {:.2f}'
...       .format(multi_layer_regressor.score(X_test, y_test)))
R2 score: 0.53

Referencias

W1992

Wolpert, David H. «Stacked generalization.» Neural networks 5.2 (1992): 241-259.