1.10. Árboles de decisión

Los árboles de decisión (DTs por sus siglas en inglés) son un método de aprendizaje supervisado no paramétrico utilizado para clasificación y regresión. El objetivo es crear un modelo que prediga el valor de una variable objetivo mediante el aprendizaje de reglas de decisión simples inferidas a partir de las características de los datos. Un árbol puede ser visto como una aproximación constante a trozos.

En el siguiente ejemplo, los árboles de decisión aprenden de los datos para aproximar una curva sinusoidal con un conjunto de reglas de decisión si-entonces-en otro caso (if-then-else). Cuanto más profundo sea el árbol, más complejas serán las reglas de decisión y más ajustado será el modelo.

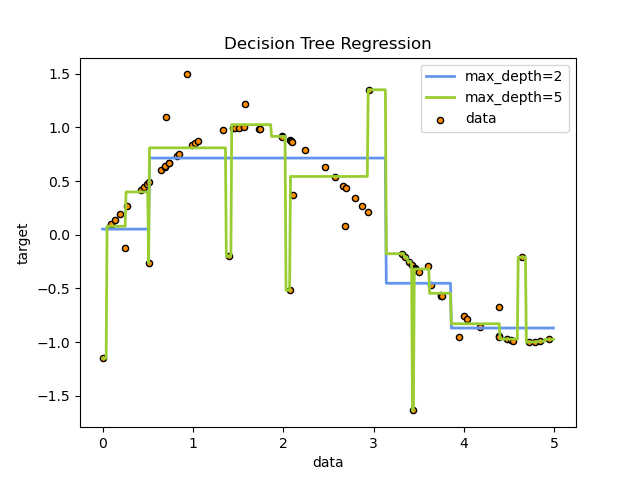
../_images/sphx_glr_plot_tree_regression_001.png

Algunas ventajas de los árboles de decisión son:

  • Sencillo de entender e interpretar. Los árboles pueden ser visualizados.

  • Requiere poca preparación de los datos. Otras técnicas a menudo requieren la normalización de datos, la creación de variables dummy y la eliminación de valores en blanco. Sin embargo, ten en cuenta que este módulo no admite valores faltantes.

  • El costo de usar el árbol (es decir, de predecir datos) es logarítmico en el número de puntos de datos utilizados para entrenar el árbol.

  • Capaz de manejar datos tanto numéricos como categóricos. Sin embargo, la implementación de scikit-learn no admite variables categóricas por ahora. Otras técnicas suelen estar especializadas en el análisis de conjuntos de datos que sólo tienen un tipo de variable. Ver algoritmos para más información.

  • Capaz de manejar problemas de salida múltiple.

  • Utiliza un modelo de caja blanca —white box model—. Si una situación dada es observable en un modelo, la explicación de la condición se explica fácilmente por lógica booleana. Por el contrario, en un modelo de caja negra —black box model— (por ejemplo, en una red neuronal artificial), los resultados pueden ser más difíciles de interpretar.

  • Es posible validar un modelo utilizando pruebas estadísticas. Eso permite tener en cuenta la fiabilidad del modelo.

  • Funciona bien incluso si sus supuestos son violados de alguna manera por el verdadero modelo a partir del cual se generaron los datos.

Las desventajas de los árboles de decisión incluyen:

  • Los algoritmos de aprendizaje de árboles de decisión pueden crear árboles demasiado complejos que no generalicen bien los datos. Esto se denomina sobreajuste. Para evitar este problema son necesarios mecanismos como la poda, establecer el número mínimo de muestras necesarias en un nodo de la hoja o establecer la profundidad máxima del árbol.

  • Los árboles de decisión pueden ser inestables porque pequeñas variaciones en los datos pueden resultar en la generación de un árbol completamente diferente. Este problema es mitigado mediante el uso de árboles de decisión dentro de un conjunto.

  • Las predicciones de los árboles de decisión no son suaves ni continuas, sino aproximaciones constantes a trozos, como se ve en la figura anterior. Por lo tanto, no son buenos para la extrapolación.

  • Se sabe que el problema del aprendizaje de un árbol de decisión óptimo es NP-completo bajo varios aspectos de optimalidad e incluso para conceptos simples. En consecuencia, los algoritmos prácticos de aprendizaje de árboles de decisión se basan en algoritmos heurísticos como el algoritmo codicioso, donde se toman decisiones localmente óptimas en cada nodo. Tales algoritmos no pueden garantizar que devuelvan el árbol de decisión globalmente óptimo. Esto puede mitigarse entrenando múltiples árboles en un algoritmo de aprendizaje de conjunto, donde las características y las muestras se muestrean aleatoriamente con reemplazo.

  • Hay conceptos difíciles de aprender porque los árboles de decisión no los expresan fácilmente, como los problemas de XOR, paridad o multiplexores.

  • Los algoritmos de aprendizaje de árboles de decisión crean árboles sesgados si algunas clases dominan. Por lo tanto, se recomienda equilibrar el conjunto de datos antes de ajustarlo con el árbol de decisión.

1.10.1. Clasificación

DecisionTreeClassifier es una clase capaz de realizar una clasificación multiclase en un conjunto de datos.

Al igual que otros clasificadores, DecisionTreeClassifier toma como entrada dos arreglos: un arreglo X, disperso o denso, de forma (n_samples, n_features) que contiene las muestras de entrenamiento, y un arreglo Y de valores enteros, de forma (n_samples,), que contiene las etiquetas de clase para las muestras de entrenamiento:

>>> from sklearn import tree
>>> X = [[0, 0], [1, 1]]
>>> Y = [0, 1]
>>> clf = tree.DecisionTreeClassifier()
>>> clf = clf.fit(X, Y)

Después de ser ajustado, el modelo puede ser utilizado para predecir la clase de muestras:

>>> clf.predict([[2., 2.]])
array([1])

En caso de que haya múltiples clases con la misma y más alta probabilidad, el clasificador predecirá la clase con el índice más bajo entre esas clases.

Como alternativa a la salida de una clase específica, se puede predecir la probabilidad de cada clase, que es la fracción de las muestras de entrenamiento de la clase en una hoja:

>>> clf.predict_proba([[2., 2.]])
array([[0., 1.]])

DecisionTreeClassifier es capaz de realizar tanto una clasificación binaria (donde las etiquetas son [-1, 1]) como una clasificación multiclase (donde las etiquetas son [0, …, K-1]).

Usando el conjunto de datos Iris, podemos construir un árbol como sigue:

>>> from sklearn.datasets import load_iris
>>> from sklearn import tree
>>> X, y = load_iris(return_X_y=True)
>>> clf = tree.DecisionTreeClassifier()
>>> clf = clf.fit(X, y)

Una vez entrenado, puedes graficar el árbol con la función plot_tree:

>>> tree.plot_tree(clf)
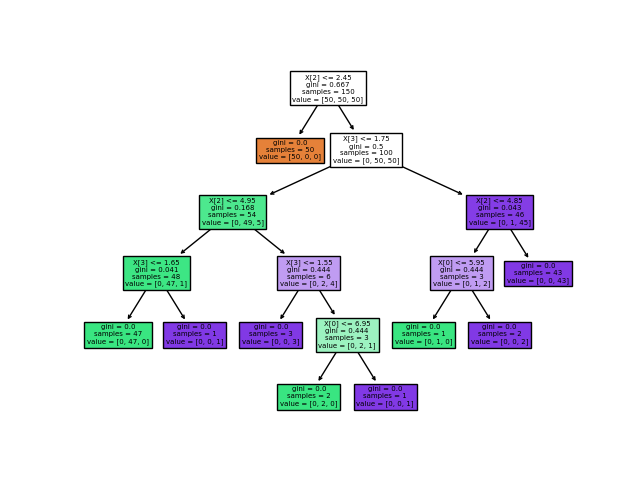
../_images/sphx_glr_plot_iris_dtc_002.png

También podemos exportar el árbol en formato Graphviz usando el exportador export_graphviz. Si utilizas el gestor de paquetes conda, los binarios de graphviz y el paquete python pueden instalarse con conda install python-graphviz.

Alternativamente, los binarios para graphviz pueden ser descargados desde la página web del proyecto graphviz, y la capa de Python instalada desde pypi con pip install graphviz.

A continuación se muestra un ejemplo de exportación en graphviz del árbol anterior entrenado en todo el conjunto de datos iris; los resultados se guardan en un archivo de salida iris.pdf:

>>> import graphviz 
>>> dot_data = tree.export_graphviz(clf, out_file=None) 
>>> graph = graphviz.Source(dot_data) 
>>> graph.render("iris")

El exportador export_graphviz también soporta una variedad de opciones estéticas, como colorear los nodos por su clase (o valor para la regresión) y usar nombres explícitos de variables y clases si así lo deseas. Los cuadernos de Jupyter también representan estos gráficos dentro de la línea automáticamente:

>>> dot_data = tree.export_graphviz(clf, out_file=None, 
...                      feature_names=iris.feature_names,  
...                      class_names=iris.target_names,  
...                      filled=True, rounded=True,  
...                      special_characters=True)  
>>> graph = graphviz.Source(dot_data)  
>>> graph
../_images/iris.svg
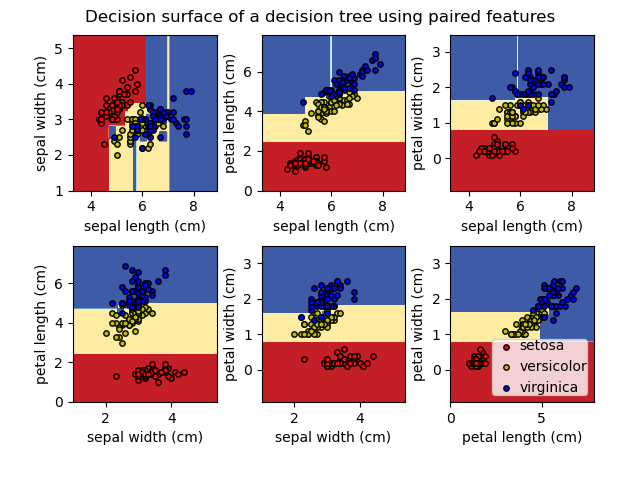
../_images/sphx_glr_plot_iris_dtc_001.png

Alternativamente, el árbol también puede exportarse en formato de texto con la función export_text. Este método no requiere la instalación de bibliotecas externas y es más compacto:

>>> from sklearn.datasets import load_iris
>>> from sklearn.tree import DecisionTreeClassifier
>>> from sklearn.tree import export_text
>>> iris = load_iris()
>>> decision_tree = DecisionTreeClassifier(random_state=0, max_depth=2)
>>> decision_tree = decision_tree.fit(iris.data, iris.target)
>>> r = export_text(decision_tree, feature_names=iris['feature_names'])
>>> print(r)
|--- petal width (cm) <= 0.80
|   |--- class: 0
|--- petal width (cm) >  0.80
|   |--- petal width (cm) <= 1.75
|   |   |--- class: 1
|   |--- petal width (cm) >  1.75
|   |   |--- class: 2

Ejemplos:

1.10.2. Regresión

../_images/sphx_glr_plot_tree_regression_001.png

Los árboles de decisión también pueden ser aplicados en problemas de regresión, utilizando la clase DecisionTreeRegressor.

Como en la configuración de la clasificación, el método de ajuste tomará como argumento los arreglos X e y, sólo que en este caso se espera que y tenga valores de punto flotante en lugar de valores enteros:

>>> from sklearn import tree
>>> X = [[0, 0], [2, 2]]
>>> y = [0.5, 2.5]
>>> clf = tree.DecisionTreeRegressor()
>>> clf = clf.fit(X, y)
>>> clf.predict([[1, 1]])
array([0.5])

Ejemplos:

1.10.3. Problemas de salida múltiple

Un problema de salida múltiple es un problema de aprendizaje supervisado con varias salidas a predecir, que es cuando Y es un arreglo 2d de la forma (n_samples, n_outputs).

Cuando no hay correlación entre las salidas, una forma muy sencilla de resolver este tipo de problema es construir n modelos independientes, es decir, uno para cada salida, y luego utilizar esos modelos para predecir independientemente cada una de las n salidas. Sin embargo, dado que es probable que los valores de salida relacionados con la misma entrada estén correlacionados, una forma a menudo mejor es construir un único modelo capaz de predecir simultáneamente todas las n salidas. En primer lugar, requiere menos tiempo de entrenamiento, ya que sólo se construye un único estimador. En segundo lugar, la precisión de la generalización del estimador resultante a menudo puede aumentar.

Con respecto a los árboles de decisión, esta estrategia puede utilizarse fácilmente para soportar los problemas de salida múltiple. Esto requiere los siguientes cambios:

  • Almacena n valores de salida en hojas, en lugar de 1;

  • Utiliza criterios de separación que calculen la reducción promedio en todas las n salidas.

Este módulo ofrece soporte para problemas de salida múltiple implementando esta estrategia tanto en DecisionTreeClassifier como en DecisionTreeRegressor. Si un árbol de decisión se ajusta a un arreglo de salida Y de la forma (n_samples, n_outputs) entonces el estimador resultante será:

  • Valores de salida n_output en predict;

  • Da salida a una lista de arreglos n_output de probabilidades de clase sobre predict_proba.

El uso de árboles de salida múltiple para regresión se demuestra en Regresión del Árbol de Decisión con salida múltiple. En este ejemplo, la entrada X es un único valor real y las salidas Y son el seno y el coseno de X.

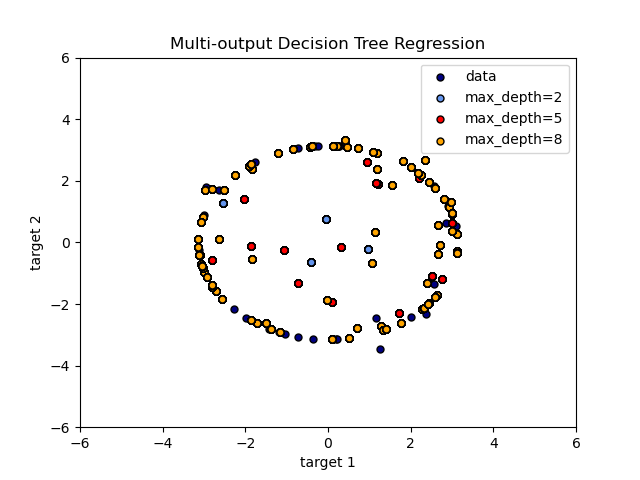
../_images/sphx_glr_plot_tree_regression_multioutput_001.png

El uso de árboles de salida múltiple para la clasificación se demuestra en Finalización facial con estimadores de salida múltiple. En este ejemplo, las entradas X son los píxeles de la mitad superior de las caras y las salidas Y son los píxeles de la mitad inferior de esas caras.

../_images/sphx_glr_plot_multioutput_face_completion_001.png

Ejemplos:

Referencias:

1.10.4. Complejidad

En general el costo de tiempo de ejecución para construir un árbol binario balanceado es \(O(n_{samples}n_{features}\log(n_{samples}))\) y el tiempo de consulta \(O(\log(n_{samples}))\). Aunque el algoritmo de construcción de árboles intenta generar árboles equilibrados, no siempre lo estarán. Asumiendo que los subárboles permanecen aproximadamente equilibrados, el costo en cada nodo consiste en buscar a través de \(O(n_{features})\) para encontrar la característica que ofrece la mayor reducción de entropía. Esto tiene un costo de \(O(n_{features}n_{samples}\log(n_{samples}))\) en cada nodo, lo que lleva a un costo total sobre todos los árboles (sumando el costo en cada nodo) de \(O(n_{features}n_{samples}^{2}\log(n_{samples}))\).

1.10.5. Consejos sobre uso práctico

  • Los árboles de decisión tienden a sobreajustarse en datos con un gran número de características. Es importante obtener la proporción adecuada de muestras con respecto al número de características, ya que un árbol con pocas muestras en un espacio de alta dimensión es muy probable que se sobreajuste.

  • Considera la posibilidad de realizar una reducción de la dimensionalidad (PCA, ICA, o Selección de características) de antemano para dar a tu árbol una mejor oportunidad de encontrar características que sean discriminatorias.

  • Comprensión de la estructura del árbol de decisiones ayudará a obtener más información sobre cómo el árbol de decisión hace las predicciones, lo cual es importante para comprender las características importantes de los datos.

  • Visualiza tu árbol mientras estás entrenando usando la función export. Usa max_depth=3 como profundidad inicial del árbol para tener una idea de cómo se ajusta a tus datos, y luego aumenta la profundidad.

  • Recuerda que el número de muestras requeridas para poblar el árbol se duplica por cada nivel adicional al que crece el árbol. Usa max_depth para controlar el tamaño del árbol para prevenir el sobreajuste.

  • Utiliza min_samples_split o min_samples_leaf para asegurarte de que las muestras múltiples informan cada decisión en el árbol, controlando qué divisiones serán consideradas. Un número muy pequeño normalmente significa que el árbol se sobreajustará, mientras que un número grande impedirá que el árbol aprenda de los datos. Prueba min_samples_leaf=5 como un valor inicial. Si el tamaño de la muestra varía considerablemente, se puede utilizar un número de punto flotante como porcentaje en estos dos parámetros. Mientras que min_samples_split puede crear hojas arbitrariamente pequeñas, min_samples_leaf garantiza que cada hoja tiene un tamaño mínimo, evitando nodos hoja de baja varianza y sobreajuste en problemas de regresión. Para la clasificación con pocas clases, min_samples_leaf=1 es a menudo la mejor opción.

    Ten en cuenta que min_samples_split considera las muestras directamente e independientemente de sample_weight, si se proporciona (por ejemplo, un nodo con m muestras ponderadas se sigue tratando como si tuviera exactamente m muestras). Considera min_weight_fraction_leaf o min_impurity_decrease si se deben tener en cuenta los pesos de las muestras en las divisiones.

  • Equilibra tu conjunto de datos antes del entrenamiento para evitar que el árbol esté sesgado hacia las clases que son dominantes. El equilibrio de las clases puede hacerse muestreando un número igual de muestras de cada clase, o preferiblemente normalizando la suma de las ponderaciones de las muestras (sample_weight) para cada clase al mismo valor. También ten en cuenta que los criterios de pre-poda basados en ponderaciones, tales como min_weight_fraction_leaf, entonces estarán menos sesgados hacia las clases dominantes que los criterios que no tienen en cuenta las ponderaciones de las muestras, como min_samples_leaf.

  • Si las muestras están ponderadas, será más fácil optimizar la estructura del árbol usando un criterio de pre-poda basado en ponderaciones como min_weight_fraction_leaf, que asegura que los nodos hoja contengan al menos una fracción de la suma total de las ponderaciones de las muestras.

  • Todos los árboles de decisión usan internamente arreglos np.float32. Si los datos de entrenamiento no están en este formato, se hará una copia del conjunto de datos.

  • Si la matriz de entrada X es muy dispersa, se recomienda convertirla a dispersa csc_matrix antes de llamar a fit y dispersa csr_matrix antes de llamar a predict. El tiempo de entrenamiento pueden ser órdenes de magnitud más rápido para una matriz de entrada dispersa en comparación con una matriz densa cuando las características tienen valores cero en la mayoría de las muestras.

1.10.6. Algoritmos de árbol: ID3, C4.5, C5.0 y CART

¿Cuáles son los diferentes algoritmos de árboles de decisión y cómo se diferencian unos de otros? ¿Cuál está implementado en scikit-learn?

ID3 (Iterative Dichotomiser 3, Dicotomizador iterativo 3) fue desarrollado en 1986 por Ross Quinlan. El algoritmo crea un árbol multidireccional, encontrando para cada nodo (es decir, de forma codiciosa) la característica categórica que producirá la mayor ganancia de información para los objetivos categóricos. Los árboles crecen hasta su tamaño máximo y luego, se suele aplicar un paso de poda para mejorar la capacidad del árbol de generalizar a los datos no vistos.

C4.5 es el sucesor de ID3 y elimina la restricción de que las características sean categóricas definiendo dinámicamente un atributo discreto (basado en variables numéricas) que particiona el valor del atributo continuo en un conjunto discreto de intervalos. C4.5 convierte los árboles entrenados (es decir, la salida del algoritmo ID3) en conjuntos de reglas if-then (si-entonces). Esa precisión de cada regla se evalúa para determinar el orden en que deben aplicarse. La poda se realiza eliminando la condición previa de una regla si la precisión de ésta mejora sin ella.

C5.0 es la última versión publicada por Quinlan bajo una licencia propietaria. Utiliza menos memoria y construye conjuntos de reglas más pequeños que C4.5, a la vez que es más preciso.

CART (Classification and Regression Trees, Árboles de Clasificación y Regresión) es muy similar a C4.5, pero difiere en que soporta variables objetivo numéricas (regresión) y no calcula conjuntos de reglas. CART construye árboles binarios usando la característica y el umbral que producen la mayor ganancia de información en cada nodo.

scikit-learn utiliza una versión optimizada del algoritmo CART; sin embargo, la implementación de scikit-learn no soporta variables categóricas por ahora.

1.10.7. Formulación matemática

Dados los vectores de entrenamiento \(x_i \in R^n\), i=1,…, l y un vector de etiquetas \(y \in R^l\), un árbol de decisión particiona recursivamente el espacio de características de tal manera que las muestras con las mismas etiquetas o valores objetivo similares se agrupan.

Deja que los datos en el nodo \(m\) sean representados por \(Q_m\) con \(N_m\) muestras. Para cada división candidata \(\theta = (j, t_m)\) que consiste en una característica \(j\) y un umbral \(t_m\), particiona los datos en subconjuntos \(Q_m^{left}(\theta)\) y \(Q_m^{right}(\theta)\)

\[ \begin{align}\begin{aligned}Q_m^{left}(\theta) = \{(x, y) | x_j <= t_m\}\\Q_m^{right}(\theta) = Q_m \setminus Q_m^{left}(\theta)\end{aligned}\end{align} \]

La calidad de una división candidata del nodo \(m\) se calcula entonces utilizando una función de impureza o función de pérdida \(H()\), cuya elección depende de la tarea que se esté resolviendo (clasificación o regresión)

\[G(Q_m, \theta) = \frac{N_m^{left}}{N_m} H(Q_m^{left}(\theta)) + \frac{N_m^{right}}{N_m} H(Q_m^{right}(\theta))\]

Selecciona los parámetros que minimizan la impureza

\[\theta^* = \operatorname{argmin}_\theta G(Q_m, \theta)\]

Recurre a los subconjuntos \(Q_m^{left}(\theta^*)\) y \(Q_m^{right}(\theta^*)\) hasta alcanzar la profundidad máxima permitida, \(N_m < \min_{samples}\) o \(N_m = 1\).

1.10.7.1. Criterios de clasificación

Si un objetivo es un resultado de clasificación que toma valores 0,1,…,K-1, para el nodo \(m\), sea

\[p_{mk} = 1/ N_m \sum_{y \in Q_m} I(y = k)\]

la proporción de observaciones de la clase k en el nodo \(m\). Si \(m\) es un nodo terminal, predict_proba para esta región se establece en \(p_{mk}\). Las medidas comunes de impureza son las siguientes.

Gini:

\[H(Q_m) = \sum_k p_{mk} (1 - p_{mk})\]

Entropía:

\[H(Q_m) = - \sum_k p_{mk} \log(p_{mk})\]

Clasificación errónea:

\[H(Q_m) = 1 - \max(p_{mk})\]

1.10.7.2. Criterios de Regresión

Si el objetivo es un valor continuo, entonces para el nodo \(m\), los criterios comunes a minimizar para determinar las ubicaciones de las futuras divisiones son el Error Cuadrático Medio (MSE o error L2), la desviación de Poisson así como el Error medio absoluto (MAE o error L1). El MSE y la desviación de Poisson establecen el valor predicho de los nodos terminales al valor medio aprendido \(\bar{y}_m\) del nodo mientras que el MAE establece el valor predicho de los nodos terminales a la mediana \(median(y)_m\).

Error Cuadrático Medio:

\[ \begin{align}\begin{aligned}\bar{y}_m = \frac{1}{N_m} \sum_{y \in Q_m} y\\H(Q_m) = \frac{1}{N_m} \sum_{y \in Q_m} (y - \bar{y}_m)^2\end{aligned}\end{align} \]

Desviación media de Poisson:

\[H(Q_m) = \frac{1}{N_m} \sum_{y \in Q_m} (y \log\frac{y}{\bar{y}_m} - y + \bar{y}_m)\]

Establecer criterion="poisson" puede ser una buena opción si tu objetivo es un conteo o una frecuencia (conteo por alguna unidad). En cualquier caso, \(y >= 0\) es una condición necesaria para utilizar este criterio. Ten en cuenta que se ajusta mucho más lento que el criterio MSE.

Error medio absoluto:

\[ \begin{align}\begin{aligned}median(y)_m = \underset{y \in Q_m}{\mathrm{median}}(y)\\H(Q_m) = \frac{1}{N_m} \sum_{y \in Q_m} |y - median(y)_m|\end{aligned}\end{align} \]

Ten en cuenta que se ajusta mucho más lento que el criterio del MSE.

1.10.8. Poda de Coste-Complejidad Mínima

La poda de coste-complejidad mínima es un algoritmo utilizado para podar un árbol para evitar el sobreajuste, descrito en el capítulo 3 de [BRE]. Este algoritmo está parametrizado por \(\alpha\ge0\) conocido como el parámetro de complejidad. El parámetro de complejidad se utiliza para definir la medida de coste-complejidad, \(R_\alpha(T)\) de un árbol \(T\) dado:

\[R_\alpha(T) = R(T) + \alpha|\widetilde{T}|\]

donde \(|\widetilde{T}|\) es el número de nodos terminales en \(T\) y \(R(T)\) se define tradicionalmente como la tasa total de clasificación errónea de los nodos terminales. Alternativamente, scikit-learn utiliza la impureza total ponderada de la muestra de los nodos terminales para \(R(T)\). Como se muestra arriba, la impureza de un nodo depende del criterio. La poda de coste-complejidad mínima encuentra el subárbol de \(T\) que minimiza \(R_alpha(T)\).

La medida de costo-complejidad de un único nodo es \(R_\alpha(t)=R(t)+\alpha\). La rama, \(T_t\), se define como un árbol donde el nodo \(t\) es su raíz. En general, la impureza de un nodo es mayor que la suma de impurezas de sus nodos terminales, \(R(T_t)<R(t)\). Sin embargo, la medida de costo-complejidad de un nodo, \(t\), y su rama, \(T_t\), pueden ser iguales dependiendo de \(alpha\). Definimos el \(alpha\) efectivo de un nodo como el valor donde son iguales, \(R_\alpha(T_t)=R_\alpha(t)\) o \(\alpha_{eff}(t)=\frac{R(t)-R(T_t)}{|T|-1}\). Un nodo no terminal con el valor más pequeño de \(\alpha_{eff}\) es el enlace más débil y será podado. Este proceso se detiene cuando el valor mínimo de \(\alpha_{eff}\) del árbol podado es mayor que el parámetro ccp_alpha.

Ejemplos:

Referencias:

BRE

L. Breiman, J. Friedman, R. Olshen, and C. Stone. Classification and Regression Trees. Wadsworth, Belmont, CA, 1984.