Árboles de decisión con poda de complejidad de costes

El clasificador DecisionTreeClassifier proporciona parámetros como min_samples_leaf y max_depth para evitar que un árbol se sobredimensione. La poda de complejidad de costes proporciona otra opción para controlar el tamaño de un árbol. En DecisionTreeClassifier, esta técnica de poda está parametrizada por el parámetro de complejidad de costes, ccp_alpha. Los valores más altos de ccp_alpha aumentan el número de nodos podados. Aquí sólo mostramos el efecto de ccp_alpha en la regularización de los árboles y cómo elegir un ccp_alpha basado en las puntuaciones de validación.

Ver también Poda de Coste-Complejidad Mínima para más detalles sobre la poda.

print(__doc__)
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_breast_cancer
from sklearn.tree import DecisionTreeClassifier

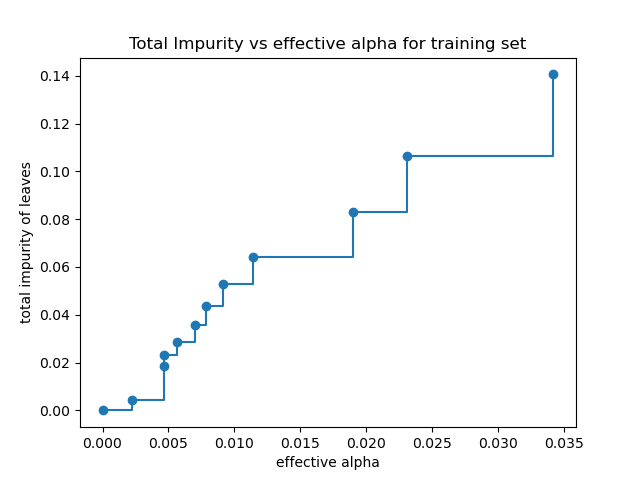
Impureza total de las hojas vs las alfas efectivas del árbol podado

La poda de complejidad de coste mínimo encuentra recursivamente el nodo con el «enlace más débil». El enlace más débil se caracteriza por un alfa efectivo, donde los nodos con el alfa efectivo más pequeño se podan primero. Para tener una idea de qué valores de ccp_alpha podrían ser apropiados, scikit-learn proporciona DecisionTreeClassifier.cost_complexity_pruning_path que devuelve los alfa efectivos y las correspondientes impurezas totales de las hojas en cada paso del proceso de poda. A medida que aumenta alfa, se poda más parte del árbol, lo que aumenta la impureza total de sus hojas.

X, y = load_breast_cancer(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

clf = DecisionTreeClassifier(random_state=0)
path = clf.cost_complexity_pruning_path(X_train, y_train)
ccp_alphas, impurities = path.ccp_alphas, path.impurities

En la siguiente gráfica se elimina el valor máximo efectivo de la alfa, ya que es el árbol trivial con sólo un nodo.

fig, ax = plt.subplots()
ax.plot(ccp_alphas[:-1], impurities[:-1], marker='o', drawstyle="steps-post")
ax.set_xlabel("effective alpha")
ax.set_ylabel("total impurity of leaves")
ax.set_title("Total Impurity vs effective alpha for training set")

Out:

Text(0.5, 1.0, 'Total Impurity vs effective alpha for training set')

A continuación, formamos un árbol de decisiones usando las alfas efectivas. El último valor en ccp_alphas es el valor alfa que limpia todo el árbol, dejando el árbol, clfs[-1], con un nodo.

clfs = []
for ccp_alpha in ccp_alphas:
    clf = DecisionTreeClassifier(random_state=0, ccp_alpha=ccp_alpha)
    clf.fit(X_train, y_train)
    clfs.append(clf)
print("Number of nodes in the last tree is: {} with ccp_alpha: {}".format(
      clfs[-1].tree_.node_count, ccp_alphas[-1]))

Out:

Number of nodes in the last tree is: 1 with ccp_alpha: 0.3272984419327777

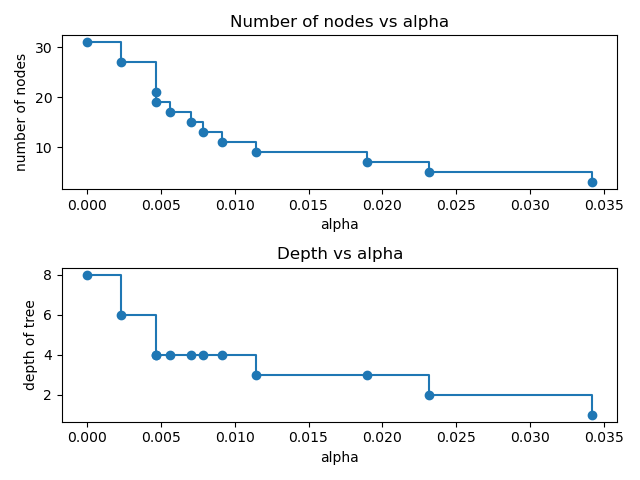
Para el resto de este ejemplo, eliminamos el último elemento en clfs y ccp_alphas, porque es el árbol trivial con un solo nodo. Aquí mostramos que el número de nodos y la profundidad del árbol disminuyen a medida que aumenta alfa.

clfs = clfs[:-1]
ccp_alphas = ccp_alphas[:-1]

node_counts = [clf.tree_.node_count for clf in clfs]
depth = [clf.tree_.max_depth for clf in clfs]
fig, ax = plt.subplots(2, 1)
ax[0].plot(ccp_alphas, node_counts, marker='o', drawstyle="steps-post")
ax[0].set_xlabel("alpha")
ax[0].set_ylabel("number of nodes")
ax[0].set_title("Number of nodes vs alpha")
ax[1].plot(ccp_alphas, depth, marker='o', drawstyle="steps-post")
ax[1].set_xlabel("alpha")
ax[1].set_ylabel("depth of tree")
ax[1].set_title("Depth vs alpha")
fig.tight_layout()

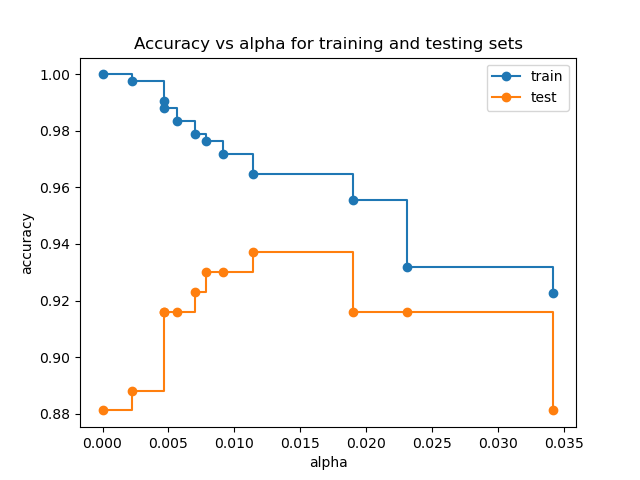
Precisión vs alfa para entrenamiento y conjuntos de pruebas

Cuando ccp_alpha se ajusta a cero y se mantienen los demás parámetros predeterminados de DecisionTreeClassifier, el árbol se ajusta en exceso, lo que lleva a una precisión de entrenamiento del 100% y una precisión de prueba del 88%. A medida que aumenta alfa, se poda una mayor parte del árbol, creando así un árbol de decisión que generaliza mejor. En este ejemplo, la configuración de ccp_alpha=0,015 maximiza la precisión de las pruebas.

train_scores = [clf.score(X_train, y_train) for clf in clfs]
test_scores = [clf.score(X_test, y_test) for clf in clfs]

fig, ax = plt.subplots()
ax.set_xlabel("alpha")
ax.set_ylabel("accuracy")
ax.set_title("Accuracy vs alpha for training and testing sets")
ax.plot(ccp_alphas, train_scores, marker='o', label="train",
        drawstyle="steps-post")
ax.plot(ccp_alphas, test_scores, marker='o', label="test",
        drawstyle="steps-post")
ax.legend()
plt.show()