Comprensión de la estructura del árbol de decisiones

La estructura del árbol de decisiones se puede analizar para obtener más información sobre la relación entre las características y el objetivo a predecir. En este ejemplo, mostramos cómo recuperar:

• la estructura del árbol binario;

• la profundidad de cada nodo y si es o no una hoja;

• los nodos que fueron alcanzados por una muestra utilizando el método decision_path;

• la hoja que fue alcanzada por una muestra utilizando el método aplicar;

• las reglas que se utilizaron para predecir una muestra;

• la ruta de decisión compartida por un grupo de muestras.

import numpy as np
from matplotlib import pyplot as plt

from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
from sklearn import tree

Entrenamiento el clasificador de árbol

Primero, nos ajustamos a un DecisionTreeClassifier usando el conjunto de datos de load_iris.

iris = load_iris()
X = iris.data
y = iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

clf = DecisionTreeClassifier(max_leaf_nodes=3, random_state=0)
clf.fit(X_train, y_train)

DecisionTreeClassifier

DecisionTreeClassifier(max_leaf_nodes=3, random_state=0)

Estructura de árbol

El clasificador de decisiones tiene un atributo llamado tree_ que permite acceder a atributos de bajo nivel como node_count, el número total de nodos, y max_depth, la profundidad máxima del árbol. También almacena toda la estructura binaria del árbol, representada como un número de matrices paralelas. El elemento i-ésimo de cada matriz contiene información sobre el nodo i. El nodo 0 es la raíz del árbol. Algunas de los arreglos sólo se aplican a las hojas o a los nodos divididos. En este caso, los valores de los nodos del otro tipo son arbitrarios. Por ejemplo, los arreglos feature y threshold sólo se aplican a los nodos divididos. Por lo tanto, los valores de los nodos hoja en estos arreglos son arbitrarios.

Entre estos arreglos tenemos:

• children_left[i]: id del hijo izquierdo del nodo i o -1 si hoja de nodo

• children_right[i]: id del hijo derecho del nodo i o -1 si hoja de nodo

• feature[i]: característica usada para dividir el nodo i

• threshold[i]: valor de umbral en el nodo i

• n_node_samples[i]: el número de muestras de entrenamiento llegando al nodo i

• impurity[i]: la impureza en el nodo i

Usando los arreglos, podemos atravesar la estructura del árbol para calcular varias propiedades. A continuación, calcularemos la profundidad de cada nodo y si es o no una hoja.

n_nodes = clf.tree_.node_count
children_left = clf.tree_.children_left
children_right = clf.tree_.children_right
feature = clf.tree_.feature
threshold = clf.tree_.threshold

node_depth = np.zeros(shape=n_nodes, dtype=np.int64)
is_leaves = np.zeros(shape=n_nodes, dtype=bool)
stack = [(0, 0)]  # start with the root node id (0) and its depth (0)
while len(stack) > 0:
    # `pop` ensures each node is only visited once
    node_id, depth = stack.pop()
    node_depth[node_id] = depth

    # If the left and right child of a node is not the same we have a split
    # node
    is_split_node = children_left[node_id] != children_right[node_id]
    # If a split node, append left and right children and depth to `stack`
    # so we can loop through them
    if is_split_node:
        stack.append((children_left[node_id], depth + 1))
        stack.append((children_right[node_id], depth + 1))
    else:
        is_leaves[node_id] = True

print("The binary tree structure has {n} nodes and has "
      "the following tree structure:\n".format(n=n_nodes))
for i in range(n_nodes):
    if is_leaves[i]:
        print("{space}node={node} is a leaf node.".format(
            space=node_depth[i] * "\t", node=i))
    else:
        print("{space}node={node} is a split node: "
              "go to node {left} if X[:, {feature}] <= {threshold} "
              "else to node {right}.".format(
                  space=node_depth[i] * "\t",
                  node=i,
                  left=children_left[i],
                  feature=feature[i],
                  threshold=threshold[i],
                  right=children_right[i]))

Out:

The binary tree structure has 5 nodes and has the following tree structure:

node=0 is a split node: go to node 1 if X[:, 3] <= 0.800000011920929 else to node 2.
        node=1 is a leaf node.
        node=2 is a split node: go to node 3 if X[:, 2] <= 4.950000047683716 else to node 4.
                node=3 is a leaf node.
                node=4 is a leaf node.

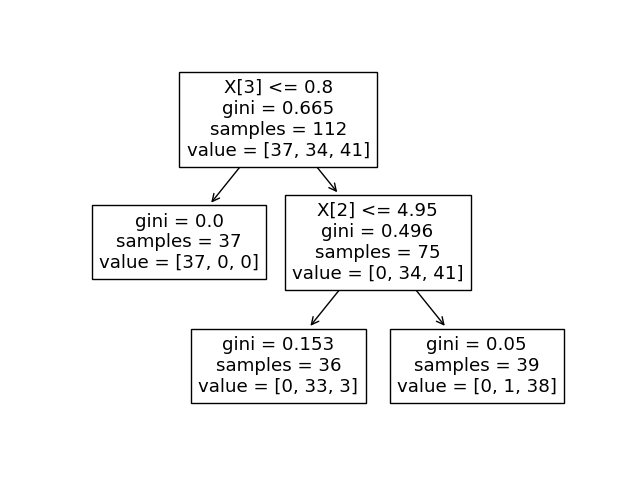
Podemos comparar la salida anterior con la trama del árbol de decisiones.

tree.plot_tree(clf)
plt.show()

Ruta de decisión

También podemos recuperar la vía de decisión de las muestras de interés. El método decision_path produce una matriz de indicador que nos permite recuperar las muestras de interés a través de los nodos. Un elemento no cero en la matriz del indicador en la posición (i, j) indica que la muestra i pasa por el nodo j. O, para una muestra i, las posiciones de los elementos no cero en la fila i de la matriz indicadora designan los ids de los nodos a través de los cuales se pasa la muestra.

Las hojas alcanzadas por muestras de interés pueden obtenerse con el método apply. Esto devuelve un arreglo de los identificadores de nodos de las hojas alcanzadas por cada muestra de interés. Usando los ids de la hoja y el decision_path podemos obtener las condiciones de división que se usaron para predecir una muestra o un grupo de muestras. Primero, hagámoslo por una muestra. Ten en cuenta que node_index es una matriz dispersa.

node_indicator = clf.decision_path(X_test)
leaf_id = clf.apply(X_test)

sample_id = 0
# obtain ids of the nodes `sample_id` goes through, i.e., row `sample_id`
node_index = node_indicator.indices[node_indicator.indptr[sample_id]:
                                    node_indicator.indptr[sample_id + 1]]

print('Rules used to predict sample {id}:\n'.format(id=sample_id))
for node_id in node_index:
    # continue to the next node if it is a leaf node
    if leaf_id[sample_id] == node_id:
        continue

    # check if value of the split feature for sample 0 is below threshold
    if (X_test[sample_id, feature[node_id]] <= threshold[node_id]):
        threshold_sign = "<="
    else:
        threshold_sign = ">"

    print("decision node {node} : (X_test[{sample}, {feature}] = {value}) "
          "{inequality} {threshold})".format(
              node=node_id,
              sample=sample_id,
              feature=feature[node_id],
              value=X_test[sample_id, feature[node_id]],
              inequality=threshold_sign,
              threshold=threshold[node_id]))

Out:

Rules used to predict sample 0:

decision node 0 : (X_test[0, 3] = 2.4) > 0.800000011920929)
decision node 2 : (X_test[0, 2] = 5.1) > 4.950000047683716)

Para un grupo de muestras, podemos determinar los nodos comunes por los que las muestras van a través.

sample_ids = [0, 1]
# boolean array indicating the nodes both samples go through
common_nodes = (node_indicator.toarray()[sample_ids].sum(axis=0) ==
                len(sample_ids))
# obtain node ids using position in array
common_node_id = np.arange(n_nodes)[common_nodes]

print("\nThe following samples {samples} share the node(s) {nodes} in the "
      "tree.".format(samples=sample_ids, nodes=common_node_id))
print("This is {prop}% of all nodes.".format(
    prop=100 * len(common_node_id) / n_nodes))

Out:

The following samples [0, 1] share the node(s) [0 2] in the tree.
This is 40.0% of all nodes.