Regresión del Árbol de Decisión con salida múltiple

Un ejemplo para ilustrar la regresión de salida múltiple con árbol de decisión.

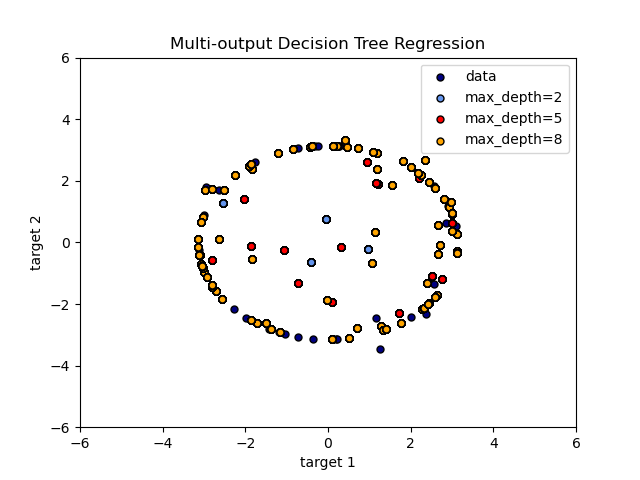
Los árboles de decisión se utilizan para predecir simultáneamente las observaciones ruidosas x e y de un círculo dado una única característica subyacente. Como resultado, aprende regresiones lineales locales aproximando el círculo.

Podemos ver que si la profundidad máxima del árbol (controlada por el parámetro max_depth) se establece demasiado alta, los árboles de decisión aprenden detalles demasiado finos de los datos de entrenamiento y aprenden del ruido, es decir, se sobreajustan.

print(__doc__)

import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor

# Create a random dataset
rng = np.random.RandomState(1)
X = np.sort(200 * rng.rand(100, 1) - 100, axis=0)
y = np.array([np.pi * np.sin(X).ravel(), np.pi * np.cos(X).ravel()]).T
y[::5, :] += (0.5 - rng.rand(20, 2))

# Fit regression model
regr_1 = DecisionTreeRegressor(max_depth=2)
regr_2 = DecisionTreeRegressor(max_depth=5)
regr_3 = DecisionTreeRegressor(max_depth=8)
regr_1.fit(X, y)
regr_2.fit(X, y)
regr_3.fit(X, y)

# Predict
X_test = np.arange(-100.0, 100.0, 0.01)[:, np.newaxis]
y_1 = regr_1.predict(X_test)
y_2 = regr_2.predict(X_test)
y_3 = regr_3.predict(X_test)

# Plot the results
plt.figure()
s = 25
plt.scatter(y[:, 0], y[:, 1], c="navy", s=s,
            edgecolor="black", label="data")
plt.scatter(y_1[:, 0], y_1[:, 1], c="cornflowerblue", s=s,
            edgecolor="black", label="max_depth=2")
plt.scatter(y_2[:, 0], y_2[:, 1], c="red", s=s,
            edgecolor="black", label="max_depth=5")
plt.scatter(y_3[:, 0], y_3[:, 1], c="orange", s=s,
            edgecolor="black", label="max_depth=8")
plt.xlim([-6, 6])
plt.ylim([-6, 6])
plt.xlabel("target 1")
plt.ylabel("target 2")
plt.title("Multi-output Decision Tree Regression")
plt.legend(loc="best")
plt.show()