Árboles de decisión multiclase AdaBoosted

Este ejemplo reproduce la Figura 1 de Zhu et al 1 y muestra cómo el boosting puede mejorar la precisión de la predicción en un problema multiclase. El conjunto de datos de clasificación se construye tomando una distribución normal estándar de diez dimensiones y definiendo tres clases separadas por esferas concéntricas anidadas de diez dimensiones, de forma que haya aproximadamente el mismo número de muestras en cada clase (cuantiles de la distribución \(\chi^2\)).

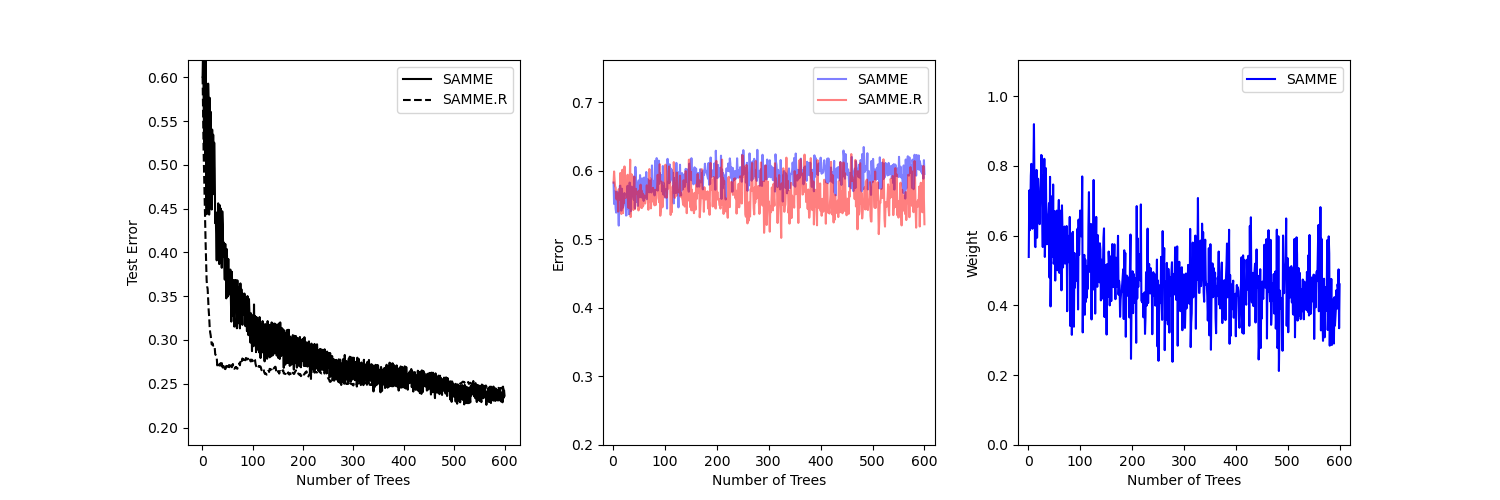
Se compara el rendimiento de los algoritmos SAMME y SAMME.R 1. SAMME.R utiliza las estimaciones de probabilidad para actualizar el modelo aditivo, mientras que SAMME sólo utiliza las clasificaciones. Como ilustra el ejemplo, el algoritmo SAMME.R suele converger más rápido que SAMME, logrando un error de prueba menor con menos iteraciones de refuerzo. El error de cada algoritmo en el conjunto de prueba después de cada iteración de refuerzo se muestra a la izquierda, el error de clasificación en el conjunto de prueba de cada árbol se muestra en el centro, y el peso de refuerzo de cada árbol se muestra a la derecha. Todos los árboles tienen un peso de uno en el algoritmo SAMME.R y, por tanto, no se muestran.

1(1,2)

10. Zhu, H. Zou, S. Rosset, T. Hastie, «Multi-class AdaBoost», 2009.

print(__doc__)

# Author: Noel Dawe <noel.dawe@gmail.com>
#
# License: BSD 3 clause

import matplotlib.pyplot as plt

from sklearn.datasets import make_gaussian_quantiles
from sklearn.ensemble import AdaBoostClassifier
from sklearn.metrics import accuracy_score
from sklearn.tree import DecisionTreeClassifier


X, y = make_gaussian_quantiles(n_samples=13000, n_features=10,
                               n_classes=3, random_state=1)

n_split = 3000

X_train, X_test = X[:n_split], X[n_split:]
y_train, y_test = y[:n_split], y[n_split:]

bdt_real = AdaBoostClassifier(
    DecisionTreeClassifier(max_depth=2),
    n_estimators=600,
    learning_rate=1)

bdt_discrete = AdaBoostClassifier(
    DecisionTreeClassifier(max_depth=2),
    n_estimators=600,
    learning_rate=1.5,
    algorithm="SAMME")

bdt_real.fit(X_train, y_train)
bdt_discrete.fit(X_train, y_train)

real_test_errors = []
discrete_test_errors = []

for real_test_predict, discrete_train_predict in zip(
        bdt_real.staged_predict(X_test), bdt_discrete.staged_predict(X_test)):
    real_test_errors.append(
        1. - accuracy_score(real_test_predict, y_test))
    discrete_test_errors.append(
        1. - accuracy_score(discrete_train_predict, y_test))

n_trees_discrete = len(bdt_discrete)
n_trees_real = len(bdt_real)

# Boosting might terminate early, but the following arrays are always
# n_estimators long. We crop them to the actual number of trees here:
discrete_estimator_errors = bdt_discrete.estimator_errors_[:n_trees_discrete]
real_estimator_errors = bdt_real.estimator_errors_[:n_trees_real]
discrete_estimator_weights = bdt_discrete.estimator_weights_[:n_trees_discrete]

plt.figure(figsize=(15, 5))

plt.subplot(131)
plt.plot(range(1, n_trees_discrete + 1),
         discrete_test_errors, c='black', label='SAMME')
plt.plot(range(1, n_trees_real + 1),
         real_test_errors, c='black',
         linestyle='dashed', label='SAMME.R')
plt.legend()
plt.ylim(0.18, 0.62)
plt.ylabel('Test Error')
plt.xlabel('Number of Trees')

plt.subplot(132)
plt.plot(range(1, n_trees_discrete + 1), discrete_estimator_errors,
         "b", label='SAMME', alpha=.5)
plt.plot(range(1, n_trees_real + 1), real_estimator_errors,
         "r", label='SAMME.R', alpha=.5)
plt.legend()
plt.ylabel('Error')
plt.xlabel('Number of Trees')
plt.ylim((.2,
         max(real_estimator_errors.max(),
             discrete_estimator_errors.max()) * 1.2))
plt.xlim((-20, len(bdt_discrete) + 20))

plt.subplot(133)
plt.plot(range(1, n_trees_discrete + 1), discrete_estimator_weights,
         "b", label='SAMME')
plt.legend()
plt.ylabel('Weight')
plt.xlabel('Number of Trees')
plt.ylim((0, discrete_estimator_weights.max() * 1.2))
plt.xlim((-20, n_trees_discrete + 20))

# prevent overlapping y-axis labels
plt.subplots_adjust(wspace=0.25)
plt.show()