Regresión de Potenciación de Gradiente

Este ejemplo demuestra la potenciación de gradiente para producir un modelo predictivo a partir de un conjunto de modelos predictivos débiles. La potenciación de gradiente puede utilizarse para problemas de regresión y clasificación. Aquí entrenaremos un modelo para abordar una tarea de regresión de la diabetes. Obtendremos los resultados de GradientBoostingRegressor con pérdidas por mínimos cuadrados y 500 árboles de regresión de profundidad 4.

Nota: Para conjuntos de datos más grandes (n_samples >= 10000), consulta HistGradientBoostingRegressor.

print(__doc__)

# Author: Peter Prettenhofer <peter.prettenhofer@gmail.com>
#         Maria Telenczuk <https://github.com/maikia>
#         Katrina Ni <https://github.com/nilichen>
#
# License: BSD 3 clause

import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, ensemble
from sklearn.inspection import permutation_importance
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split

Cargar los datos

Primero tenemos que cargar los datos.

diabetes = datasets.load_diabetes()
X, y = diabetes.data, diabetes.target

Preprocesamiento de datos

A continuación, dividiremos nuestro conjunto de datos para utilizar el 90% para el entrenamiento y dejar el resto para las pruebas. También estableceremos los parámetros del modelo de regresión. Puedes jugar con estos parámetros para ver cómo cambian los resultados.

n_estimadores : el número de etapas de potenciación (boosting) que se realizarán. Más adelante, graficaremos la desviación en función de las iteraciones de potenciación.

max_depth : limita el número de nodos del árbol. El mejor valor depende de la interacción de las variables de entrada.

min_samples_split : el número mínimo de muestras necesarias para dividir un nodo interno.

learning_rate : cuánto se reducirá la contribución de cada árbol.

loss : función de pérdida a optimizar. En este caso se utiliza la función de mínimos cuadrados, sin embargo, hay muchas otras opciones (ver GradientBoostingRegressor ).

X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.1, random_state=13)

params = {'n_estimators': 500,
          'max_depth': 4,
          'min_samples_split': 5,
          'learning_rate': 0.01,
          'loss': 'ls'}

Ajustar modelo de regresión

Ahora vamos a iniciar los regresores de potenciación de gradiente y a ajustarlos con nuestros datos de entrenamiento. Veamos también el error cuadrático medio en los datos de prueba.

reg = ensemble.GradientBoostingRegressor(**params)
reg.fit(X_train, y_train)

mse = mean_squared_error(y_test, reg.predict(X_test))
print("The mean squared error (MSE) on test set: {:.4f}".format(mse))

Out:

The mean squared error (MSE) on test set: 3017.9419

Graficar la desviación del entrenamiento

Por último, visualizaremos los resultados. Para ello, primero calcularemos la desviación del conjunto de pruebas y luego la representaremos en función de las iteraciones de la potenciación.

test_score = np.zeros((params['n_estimators'],), dtype=np.float64)
for i, y_pred in enumerate(reg.staged_predict(X_test)):
    test_score[i] = reg.loss_(y_test, y_pred)

fig = plt.figure(figsize=(6, 6))
plt.subplot(1, 1, 1)
plt.title('Deviance')
plt.plot(np.arange(params['n_estimators']) + 1, reg.train_score_, 'b-',
         label='Training Set Deviance')
plt.plot(np.arange(params['n_estimators']) + 1, test_score, 'r-',
         label='Test Set Deviance')
plt.legend(loc='upper right')
plt.xlabel('Boosting Iterations')
plt.ylabel('Deviance')
fig.tight_layout()
plt.show()

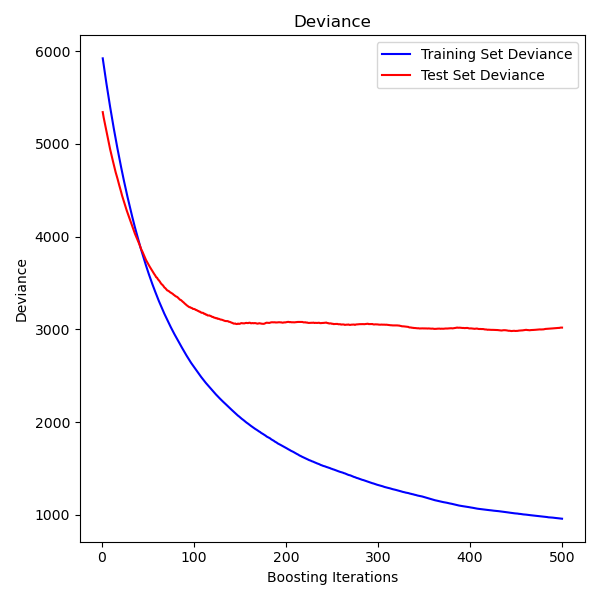
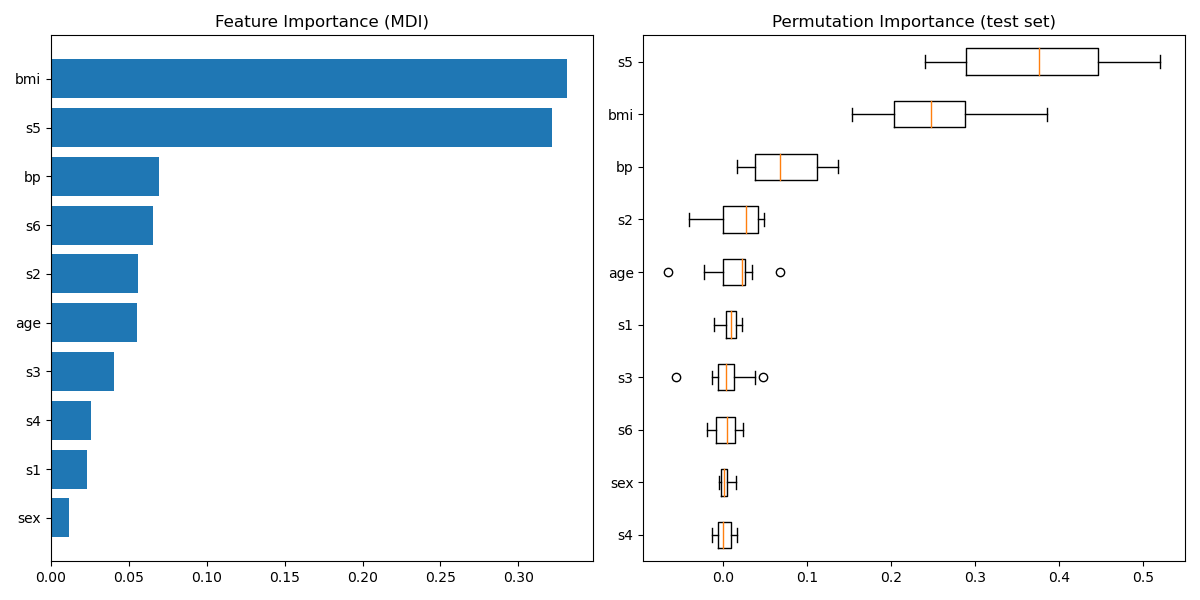
Graficar la importancia de las características

Con cuidado, las importancias de las características basadas en las impurezas pueden ser no representativas para las características de alta cardinalidad (muchos valores únicos). Como alternativa, las importancias de permutación de reg pueden ser calculadas en un conjunto de prueba reservado. Ver Importancia de la característica de permutación para más detalles.

En este ejemplo, los métodos basados en las impurezas y en la permutación identifican los mismos 2 rasgos fuertemente predictivos, pero no en el mismo orden. La tercera característica más predictiva, «bp», también es la misma para los 2 métodos. El resto de características son menos predictivas y las barras de error del gráfico de permutación muestran que se solapan con 0.

feature_importance = reg.feature_importances_
sorted_idx = np.argsort(feature_importance)
pos = np.arange(sorted_idx.shape[0]) + .5
fig = plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.barh(pos, feature_importance[sorted_idx], align='center')
plt.yticks(pos, np.array(diabetes.feature_names)[sorted_idx])
plt.title('Feature Importance (MDI)')

result = permutation_importance(reg, X_test, y_test, n_repeats=10,
                                random_state=42, n_jobs=2)
sorted_idx = result.importances_mean.argsort()
plt.subplot(1, 2, 2)
plt.boxplot(result.importances[sorted_idx].T,
            vert=False, labels=np.array(diabetes.feature_names)[sorted_idx])
plt.title("Permutation Importance (test set)")
fig.tight_layout()
plt.show()