Estimador único frente a empaquetado (bagging): descomposición sesgo-varianza

Este ejemplo ilustra y compara la descomposición sesgo-varianza del error cuadrático medio esperado de un único estimador frente a un conjunto de ensemble de empaquetados (bagging).

En regresión, el error medio cuadrático esperado de un estimador puede descomponerse en términos de sesgo, varianza y ruido. En promedio sobre conjuntos de datos del problema de regresión, el término de sesgo mide la cantidad media en que las predicciones del estimador difieren de las predicciones del mejor estimador posible para el problema (es decir, el modelo de Bayes). El término de varianza mide la variabilidad de las predicciones del estimador cuando se ajusta a diferentes instancias LS del problema. Por último, el ruido mide la parte irreducible del error que se debe a la variabilidad de los datos.

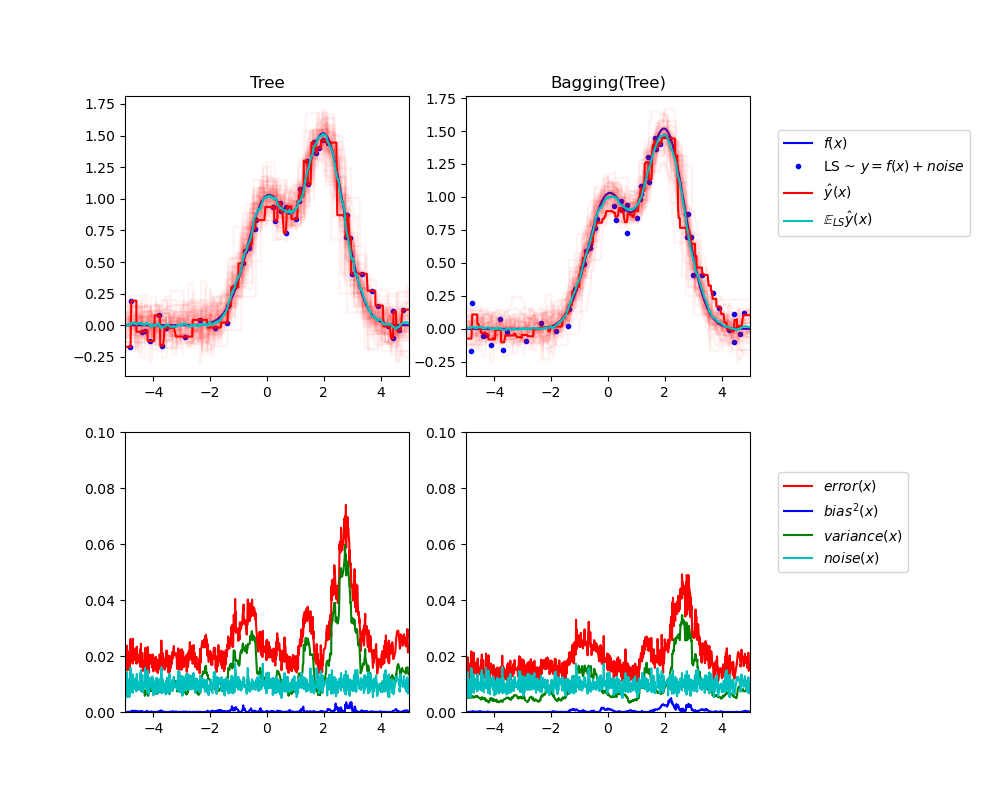
La figura superior izquierda ilustra las predicciones (en rojo oscuro) de un único árbol de decisión entrenado sobre un conjunto de datos aleatorio LS (los puntos azules) de un problema de regresión 1d de laboratorio. También ilustra las predicciones (en rojo claro) de otros árboles de decisión individuales entrenados sobre otras (y diferentes) instancias aleatorias LS del problema. Intuitivamente, el término de varianza aquí corresponde a la anchura del haz de predicciones (en rojo claro) de los estimadores individuales. Cuanto mayor sea la varianza, más sensibles serán las predicciones de x a pequeños cambios en el conjunto de entrenamiento. El término de sesgo corresponde a la diferencia entre la predicción media del estimador (en cian) y el mejor modelo posible (en azul oscuro). En este problema, podemos observar que el sesgo es bastante bajo (tanto la curva cian como la azul están próximas entre sí) mientras que la varianza es grande (el haz rojo es bastante ancho).

La figura inferior izquierda muestra la descomposición puntual del error cuadrático medio esperado de un solo árbol de decisión. Confirma que el término de sesgo (en azul) es bajo mientras que la varianza es grande (en verde). También ilustra la parte de ruido del error que, como se esperaba, parece ser constante y estar en torno a 0,01.

Las figuras de la derecha corresponden a los mismos gráficos pero utilizando en su lugar un conjunto de árboles de decisión de ensemble de empaquetados (bagging ensemble). En ambas figuras, podemos observar que el término de sesgo es mayor que en el caso anterior. En la figura superior derecha, la diferencia entre la predicción media (en cian) y el mejor modelo posible es mayor (por ejemplo, nótese el desplazamiento alrededor de x=2). En la figura inferior derecha, la curva de sesgo también es ligeramente superior a la de la figura inferior izquierda. Sin embargo, en términos de varianza, el haz de predicciones es más estrecho, lo que sugiere que la varianza es menor. De hecho, como confirma la figura inferior derecha, el término de varianza (en verde) es menor que el de los árboles de decisión simples. En general, la descomposición sesgo-varianza ya no es la misma. La compensación es mejor para el empaquetado (bagging): promediar varios árboles de decisión ajustados en copias bootstrap del conjunto de datos aumenta ligeramente el término de sesgo pero permite una mayor reducción de la varianza, lo que resulta en un error cuadrático medio más bajo (compare las curvas rojas en las figuras inferiores). El resultado del script también confirma esta intuición. El error total del conjunto de bolsas es menor que el error total de un solo árbol de decisión, y esta diferencia se debe principalmente a la reducción de la varianza.

Para más detalles sobre la descomposición sesgo-varianza, véase la sección 7.3 de 1.

Referencias

1

T. Hastie, R. Tibshirani and J. Friedman, «Elements of Statistical Learning», Springer, 2009.

Out:

Tree: 0.0255 (error) = 0.0003 (bias^2)  + 0.0152 (var) + 0.0098 (noise)
Bagging(Tree): 0.0196 (error) = 0.0004 (bias^2)  + 0.0092 (var) + 0.0098 (noise)

print(__doc__)

# Author: Gilles Louppe <g.louppe@gmail.com>
# License: BSD 3 clause

import numpy as np
import matplotlib.pyplot as plt

from sklearn.ensemble import BaggingRegressor
from sklearn.tree import DecisionTreeRegressor

# Settings
n_repeat = 50       # Number of iterations for computing expectations
n_train = 50        # Size of the training set
n_test = 1000       # Size of the test set
noise = 0.1         # Standard deviation of the noise
np.random.seed(0)

# Change this for exploring the bias-variance decomposition of other
# estimators. This should work well for estimators with high variance (e.g.,
# decision trees or KNN), but poorly for estimators with low variance (e.g.,
# linear models).
estimators = [("Tree", DecisionTreeRegressor()),
              ("Bagging(Tree)", BaggingRegressor(DecisionTreeRegressor()))]

n_estimators = len(estimators)


# Generate data
def f(x):
    x = x.ravel()

    return np.exp(-x ** 2) + 1.5 * np.exp(-(x - 2) ** 2)


def generate(n_samples, noise, n_repeat=1):
    X = np.random.rand(n_samples) * 10 - 5
    X = np.sort(X)

    if n_repeat == 1:
        y = f(X) + np.random.normal(0.0, noise, n_samples)
    else:
        y = np.zeros((n_samples, n_repeat))

        for i in range(n_repeat):
            y[:, i] = f(X) + np.random.normal(0.0, noise, n_samples)

    X = X.reshape((n_samples, 1))

    return X, y


X_train = []
y_train = []

for i in range(n_repeat):
    X, y = generate(n_samples=n_train, noise=noise)
    X_train.append(X)
    y_train.append(y)

X_test, y_test = generate(n_samples=n_test, noise=noise, n_repeat=n_repeat)

plt.figure(figsize=(10, 8))

# Loop over estimators to compare
for n, (name, estimator) in enumerate(estimators):
    # Compute predictions
    y_predict = np.zeros((n_test, n_repeat))

    for i in range(n_repeat):
        estimator.fit(X_train[i], y_train[i])
        y_predict[:, i] = estimator.predict(X_test)

    # Bias^2 + Variance + Noise decomposition of the mean squared error
    y_error = np.zeros(n_test)

    for i in range(n_repeat):
        for j in range(n_repeat):
            y_error += (y_test[:, j] - y_predict[:, i]) ** 2

    y_error /= (n_repeat * n_repeat)

    y_noise = np.var(y_test, axis=1)
    y_bias = (f(X_test) - np.mean(y_predict, axis=1)) ** 2
    y_var = np.var(y_predict, axis=1)

    print("{0}: {1:.4f} (error) = {2:.4f} (bias^2) "
          " + {3:.4f} (var) + {4:.4f} (noise)".format(name,
                                                      np.mean(y_error),
                                                      np.mean(y_bias),
                                                      np.mean(y_var),
                                                      np.mean(y_noise)))

    # Plot figures
    plt.subplot(2, n_estimators, n + 1)
    plt.plot(X_test, f(X_test), "b", label="$f(x)$")
    plt.plot(X_train[0], y_train[0], ".b", label="LS ~ $y = f(x)+noise$")

    for i in range(n_repeat):
        if i == 0:
            plt.plot(X_test, y_predict[:, i], "r", label=r"$\^y(x)$")
        else:
            plt.plot(X_test, y_predict[:, i], "r", alpha=0.05)

    plt.plot(X_test, np.mean(y_predict, axis=1), "c",
             label=r"$\mathbb{E}_{LS} \^y(x)$")

    plt.xlim([-5, 5])
    plt.title(name)

    if n == n_estimators - 1:
        plt.legend(loc=(1.1, .5))

    plt.subplot(2, n_estimators, n_estimators + n + 1)
    plt.plot(X_test, y_error, "r", label="$error(x)$")
    plt.plot(X_test, y_bias, "b", label="$bias^2(x)$"),
    plt.plot(X_test, y_var, "g", label="$variance(x)$"),
    plt.plot(X_test, y_noise, "c", label="$noise(x)$")

    plt.xlim([-5, 5])
    plt.ylim([0, 0.1])

    if n == n_estimators - 1:

        plt.legend(loc=(1.1, .5))

plt.subplots_adjust(right=.75)
plt.show()