Soporte de características categóricas en Potenciación del Gradiente (Gradient Boosting)

En este ejemplo, compararemos los tiempos de entrenamiento y el rendimiento de la predicción de HistGradientBoostingRegressor con diferentes estrategias de codificación de características categóricas. En particular, evaluaremos:

• dejando de lado las características categóricas

• usando un OneHotEncoder

• utilizando un OrdinalEncoder y tratar las categorías como cantidades ordenadas y equidistantes

• utilizando un OrdinalEncoder y confiar en el native category support del estimador HistGradientBoostingRegressor.

Trabajaremos con el conjunto de datos de Ames Lowa Housing, que consta de características numéricas y categóricas, y cuyo objetivo es el precio de venta de las viviendas.

print(__doc__)

Cargar conjunto de datos Ames Housing

En primer lugar, cargamos los datos de Ames Housing como un dataframe de Pandas. Las características son categóricas o numéricas:

from sklearn.datasets import fetch_openml

X, y = fetch_openml(data_id=41211, as_frame=True, return_X_y=True)

n_categorical_features = (X.dtypes == 'category').sum()
n_numerical_features = (X.dtypes == 'float').sum()
print(f"Number of samples: {X.shape[0]}")
print(f"Number of features: {X.shape[1]}")
print(f"Number of categorical features: {n_categorical_features}")
print(f"Number of numerical features: {n_numerical_features}")

Out:

/home/mapologo/miniconda3/envs/sklearn/lib/python3.9/site-packages/scikit_learn-0.24.1-py3.9-linux-x86_64.egg/sklearn/datasets/_openml.py:849: UserWarning: Version 1 of dataset ames-housing is inactive, meaning that issues have been found in the dataset. Try using a newer version from this URL: https://www.openml.org/data/v1/download/20649135/ames-housing.arff
  warn("Version {} of dataset {} is inactive, meaning that issues have "
Number of samples: 2930
Number of features: 80
Number of categorical features: 46
Number of numerical features: 34

Estimador de potenciación de gradiente con características categóricas eliminadas

Como línea de base, creamos un estimador en el que se eliminan las características categóricas:

from sklearn.experimental import enable_hist_gradient_boosting  # noqa
from sklearn.ensemble import HistGradientBoostingRegressor
from sklearn.pipeline import make_pipeline
from sklearn.compose import make_column_transformer
from sklearn.compose import make_column_selector

dropper = make_column_transformer(
    ('drop', make_column_selector(dtype_include='category')),
    remainder='passthrough')
hist_dropped = make_pipeline(dropper,
                             HistGradientBoostingRegressor(random_state=42))

Estimador de potenciación de gradiente con codificación one-hot

A continuación, creamos un pipeline que codificará las características categóricas con un one-hot y dejará pasar el resto de los datos numéricos:

from sklearn.preprocessing import OneHotEncoder

one_hot_encoder = make_column_transformer(
    (OneHotEncoder(sparse=False, handle_unknown='ignore'),
     make_column_selector(dtype_include='category')),
    remainder='passthrough')

hist_one_hot = make_pipeline(one_hot_encoder,
                             HistGradientBoostingRegressor(random_state=42))

Estimador de potenciación de gradiente (gradient boosting) con codificación one-hot

A continuación, creamos un pipeline que tratará las características categóricas como si fueran cantidades ordenadas, es decir, las categorías se codificarán como 0, 1, 2, etc., y se tratarán como características continuas.

from sklearn.preprocessing import OrdinalEncoder
import numpy as np

ordinal_encoder = make_column_transformer(
    (OrdinalEncoder(handle_unknown='use_encoded_value', unknown_value=np.nan),
     make_column_selector(dtype_include='category')),
    remainder='passthrough')

hist_ordinal = make_pipeline(ordinal_encoder,
                             HistGradientBoostingRegressor(random_state=42))

Estimador de potenciación de gradiente con soporte categórico nativo

Ahora creamos un estimador HistGradientBoostingRegressor que manejará de forma nativa las características categóricas. Este estimador no tratará las características categóricas como cantidades ordenadas.

Dado que el HistGradientBoostingRegressor requiere que los valores de las categorías se codifiquen en [0, n_unique_categories - 1], seguimos dependiendo de un OrdinalEncoder para preprocesar los datos.

La principal diferencia entre este pipeline y el anterior es que en éste, dejamos que el HistGradientBoostingRegressor sepa qué características son categóricas.

# The ordinal encoder will first output the categorical features, and then the
# continuous (passed-through) features
categorical_mask = ([True] * n_categorical_features +
                    [False] * n_numerical_features)
hist_native = make_pipeline(
    ordinal_encoder,
    HistGradientBoostingRegressor(random_state=42,
                                  categorical_features=categorical_mask)
)

Comparación de modelos

Por último, evaluamos los modelos mediante validación cruzada. Aquí comparamos el rendimiento de los modelos en términos de mean_absolute_percentage_error y tiempos de ajuste.

from sklearn.model_selection import cross_validate
import matplotlib.pyplot as plt

scoring = "neg_mean_absolute_percentage_error"
dropped_result = cross_validate(hist_dropped, X, y, cv=3, scoring=scoring)
one_hot_result = cross_validate(hist_one_hot, X, y, cv=3, scoring=scoring)
ordinal_result = cross_validate(hist_ordinal, X, y, cv=3, scoring=scoring)
native_result = cross_validate(hist_native, X, y, cv=3, scoring=scoring)


def plot_results(figure_title):
    fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 8))

    plot_info = [('fit_time', 'Fit times (s)', ax1, None),
                 ('test_score', 'Mean Absolute Percentage Error', ax2,
                  (0, 0.20))]

    x, width = np.arange(4), 0.9
    for key, title, ax, y_limit in plot_info:
        items = [dropped_result[key], one_hot_result[key], ordinal_result[key],
                 native_result[key]]
        ax.bar(x, [np.mean(np.abs(item)) for item in items],
               width, yerr=[np.std(item) for item in items],
               color=['C0', 'C1', 'C2', 'C3'])
        ax.set(xlabel='Model', title=title, xticks=x,
               xticklabels=["Dropped", "One Hot", "Ordinal", "Native"],
               ylim=y_limit)
    fig.suptitle(figure_title)


plot_results("Gradient Boosting on Adult Census")

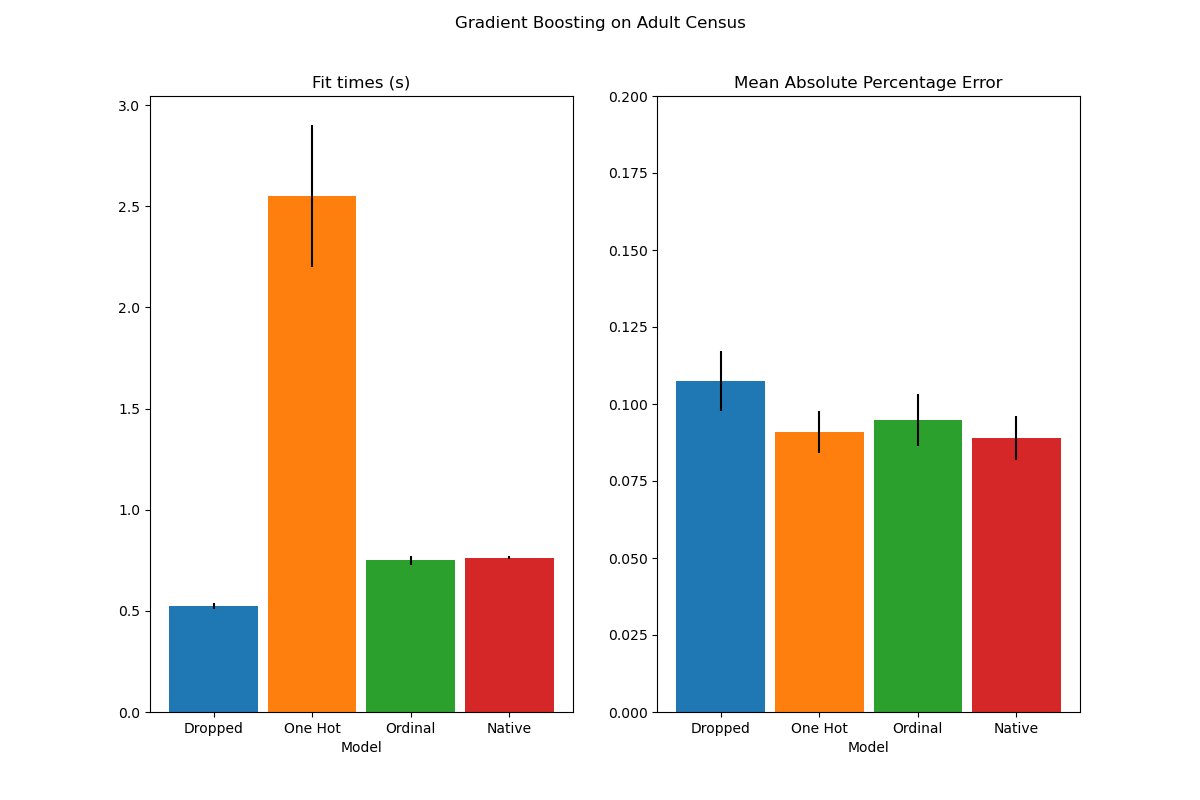
Vemos que el modelo con datos codificados one-hot es, con mucho, el más lento. Esto es de esperar, ya que la codificación one-hot crea una característica adicional por cada valor de categoría (para cada característica categórica), y por lo tanto hay que considerar más puntos de división durante el ajuste. En teoría, esperamos que el manejo nativo de las características categóricas sea ligeramente más lento que el tratamiento de las categorías como cantidades ordenadas (“Ordinal”), ya que el manejo nativo requiere sorting categories. Sin embargo, los tiempos de ajuste deberían ser cercanos cuando el número de categorías es pequeño, y esto puede no reflejarse siempre en la práctica.

En cuanto al rendimiento de la predicción, la supresión de las características categóricas da lugar a un rendimiento inferior. Los tres modelos que utilizan características categóricas tienen tasas de error comparables, con una ligera ventaja para el tratamiento nativo.

Limitar el número de divisiones (splits)

En general, cabe esperar predicciones más pobres a partir de los datos codificados one-hot, especialmente cuando la profundidad del árbol o el número de nodos son limitados: con los datos codificados con un solo punto, se necesitan más puntos de división, es decir, más profundidad, para recuperar una división equivalente a la que podría obtenerse en un solo punto de división con la manipulación nativa.

Esto también es cierto cuando las categorías se tratan como cantidades ordinales: si las categorías son A..F y la mejor división es ACF - BDE, el modelo de codificador one-hot necesitará 3 puntos de división (uno por categoría en el nodo izquierdo), y el modelo ordinal no nativo necesitará 4 divisiones: 1 división para aislar A, 1 división para aislar F y 2 divisiones para aislar C de BCDE.

La diferencia de rendimiento de los modelos en la práctica dependerá del conjunto de datos y de la flexibilidad de los árboles.

Para ver esto, volvamos a realizar el mismo análisis con modelos de subajuste en los que limitamos artificialmente el número total de divisiones limitando tanto el número de árboles como la profundidad de cada uno de ellos.

for pipe in (hist_dropped, hist_one_hot, hist_ordinal, hist_native):
    pipe.set_params(histgradientboostingregressor__max_depth=3,
                    histgradientboostingregressor__max_iter=15)

dropped_result = cross_validate(hist_dropped, X, y, cv=3, scoring=scoring)
one_hot_result = cross_validate(hist_one_hot, X, y, cv=3, scoring=scoring)
ordinal_result = cross_validate(hist_ordinal, X, y, cv=3, scoring=scoring)
native_result = cross_validate(hist_native, X, y, cv=3, scoring=scoring)

plot_results("Gradient Boosting on Adult Census (few and small trees)")

plt.show()

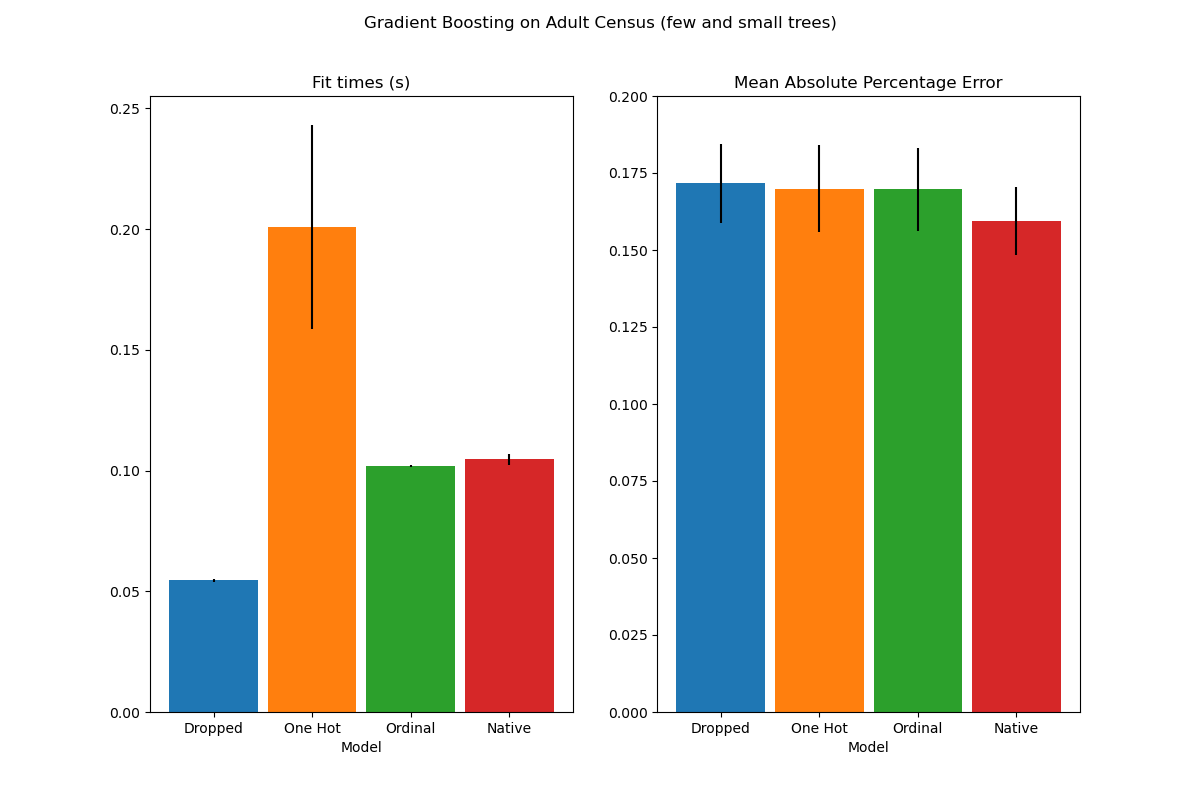
Los resultados de estos modelos de subajuste confirman nuestra intuición anterior: la estrategia de tratamiento de las categorías nativas es la que mejor funciona cuando el presupuesto de división es limitado. Las otras dos estrategias (codificación one-hot y tratamiento de las categorías como valores ordinales) conducen a valores de error comparables a los del modelo de referencia que simplemente elimina las características categóricas.