2.2. Aprendizaje múltiple¶
El aprendizaje múltiple es un acercamiento a la reducción de dimensionalidad no lineal. Los algoritmos para esta tarea se basan en la idea de que la dimensionalidad de muchos conjuntos de datos es sólo alta artificialmente.
2.2.1. Introducción¶
Los conjuntos de datos de alta dimensión pueden ser muy difíciles de visualizar. Mientras que los datos en dos o tres dimensiones se pueden graficar para mostrar la estructura inherente de los datos, los graficos equivalentes de alta dimensión son mucho menos intuitivos. Para ayudar a la visualización de la estructura de un conjunto de datos, la dimensión debe ser reducida de alguna forma.
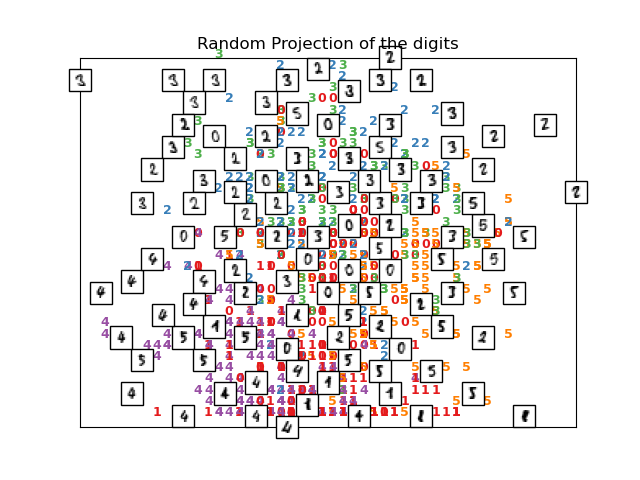
La forma mas sencilla de lograr esta reducción de dimensionalidad es tomando una proyección aleatoria de los datos. Aunque esto permite cierto grado de visualización de la estructura de datos, la aleatoridad de la elección deja mucho que ser deseado. En una proyección aleatoria, es probable que las estructuras mas interesantes dentro de los datos se pierdan.
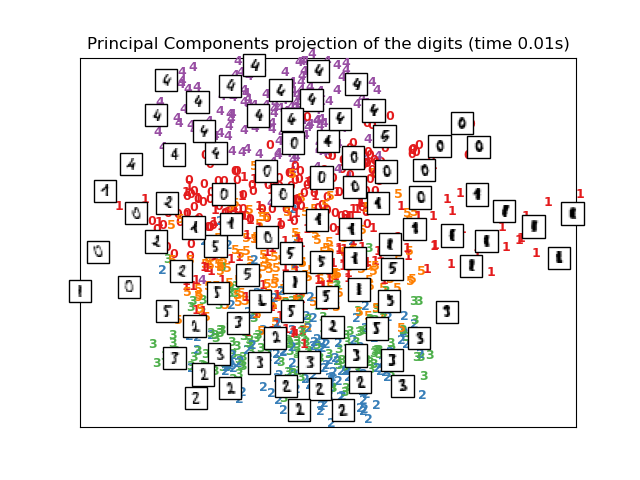
Para abordar esta inquietud, un número de frameworks de reducción de dimensionalidad lineal supervisada y no supervisada han sido diseñados, como el Análisis de Componentes Principales (APC, o PCA en inglés), Análisis de Componentes Independientes, Análisis Discriminante Lineal, y otros. Estos algoritmos definen rubricas especificas para escoger una proyección lineal «interesante» de los datos. Estos métodos pueden ser poderosos, pero frecuentemente pierden estructuras importantes no lineales en los datos.
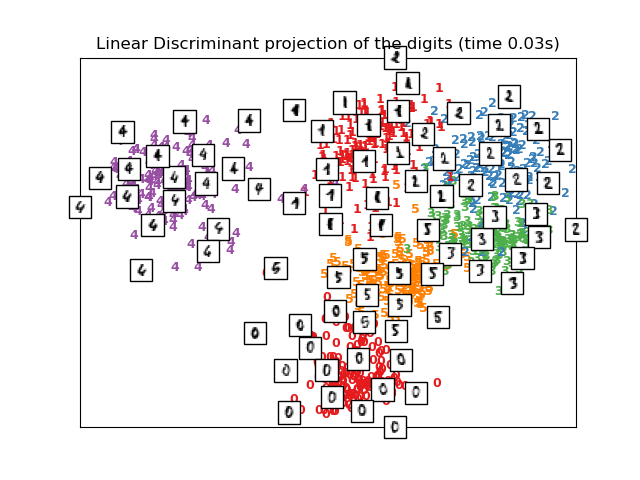
El aprendizaje múltiple puede ser considerado como un intento de generalizar frameworks lineales como el APC para ser sensibles a estructuras no lineales en los datos. Aunque existen variantes supervisadas, el problema típico de aprendizaje múltiple es sin supervisión, aprende la estructura de alta-dimensionalidad de los datos dentro de los propios datos, sin el uso de clasificaciones predeterminadas.
Ejemplos:
Vea Aprendizaje múltiple sobre dígitos manuscritos: Incrustación local lineal, Isomap… para un ejemplo de reducción de dimensionalidad en dígitos escritos a mano.
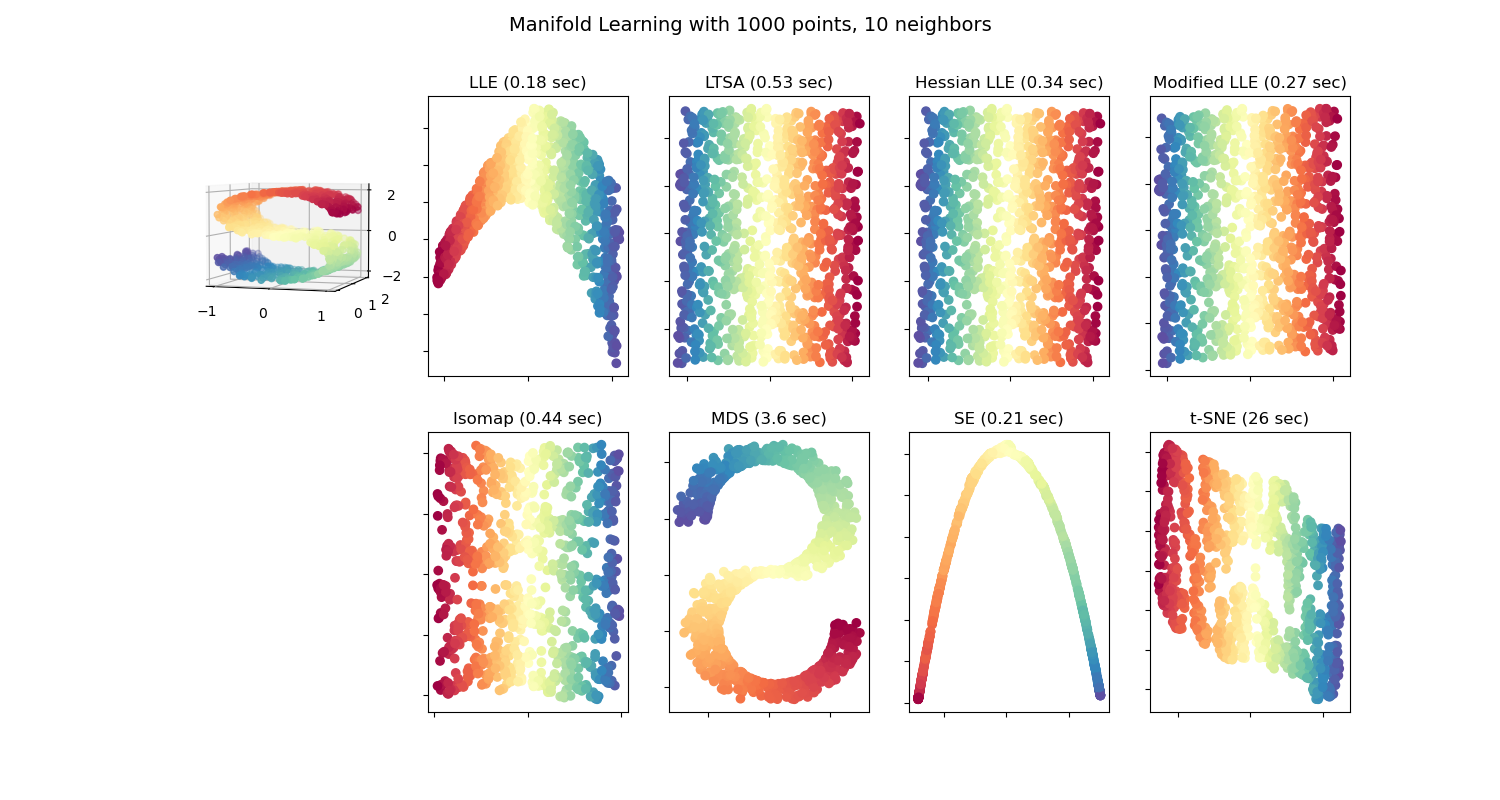
Vea Comparación de los métodos de Aprendizaje Múltiple para un ejemplo de reducción de dimensionalidad en un conjunto de datos «S-curve» de juguete.
Las implementaciones del aprendizaje múltiple disponibles en scikit-learn se resumen a continuación
2.2.2. Isomap¶
Uno de los acercamientos más antiguos al aprendizaje múltiple es el algoritmo Isomap, abreviatura de Mapeo Isometrico. Isomap puede ser visto como una extensión del Escalado Multi-dimensional (EMD, o MDS en inglés) o APC núcleo. Isomap busca un embedding de dimensionalidad mas baja que mantiene distancias geodésicas entre todos los puntos. Se puede utilizar Isomap con el objeto Isomap.
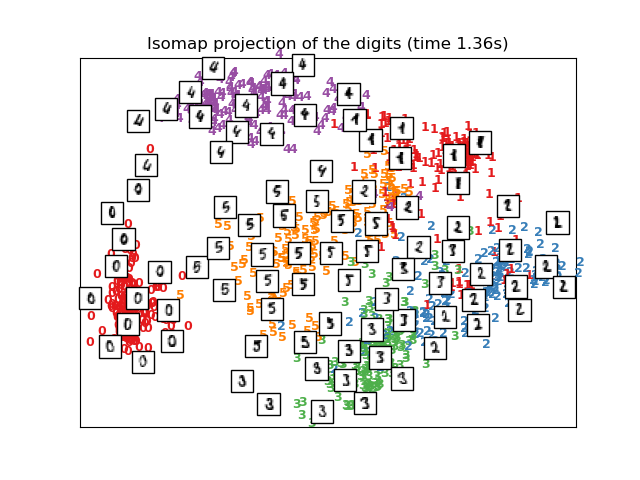
2.2.2.1. Complejidad¶
El algoritmo Isomap comprende tres etapas:
Búsqueda de vecino más cercana. Isomap utiliza
BallTreepara una búsqueda eficiente de vecinos. El costo es de aproximadamente \(O[D \log(k) N \log(N)]\), para \(k\) vecinos más cercanos de \(N\) en \(D\) dimensiones.Búsqueda en el gráfico del camino más corto. Los algoritmos conocidos más eficientes para esto son el Algoritmo de Dijkstra, el cual es aproximadamente \(O[N^2(k + \log(N))]\), o el Algoritmo Floyd-Warshall, que es \(O[N^3]\). El algoritmo puede ser seleccionado por el usuario con la palabra clave
path_methoddeIsomap. Si se deja sin especificar, el código intenta escoger el mejor algoritmo para los dato de entrada.Descomposición parcial del autovalor. El embedding está codificado en los autovectores correspondiendo a los autovalores más altos \(d\) del núcleo isomap \(N \times N\). Para un solucionador denso, el costo es aproximadamente \(O[d N^2]\). Este costo puede frecuentemente ser mejorado utilizando el solucionador
ARPACK. El autosolucionador puede ser especificado por el usuario con la palabra claveeigen_solverdeIsomap. Si se deja sin especificar, el código intenta escoger el mejor algoritmo para los datos de entrada.
La complejidad general de Isomap es \(O[D \\log(k) N \\log(N)] + O[N^2(k + \\log(N))] + O[d N^2]\).
\(N\) : número de puntos de datos de entrenamiento
\(D\): dimensión de entrada
\(k\) : número de vecinos más cercanos
\(d\): dimensión de salida
Referencias:
«A global geometric framework for nonlinear dimensionality reduction» Tenenbaum, J.B.; De Silva, V.; & Langford, J.C. Science 290 (5500)
2.2.3. Embedding localmente lineal¶
El embedding localmente lineal (ELL, o LLE en inglés) busca una proyección de menor dimensionalidad de los datos que preserva distancias dentro de los vecindarios locales. Puede ser pensado como una serie de Análisis de Componentes Principales, los cuales son comparados globalmente para encontrar la mejor incrustación no lineal.
El embedding localmente lineal puede ser realizado con la función locally_linear_embedding o su contraparte orientada a objetos LocallyLinearEmbedding.
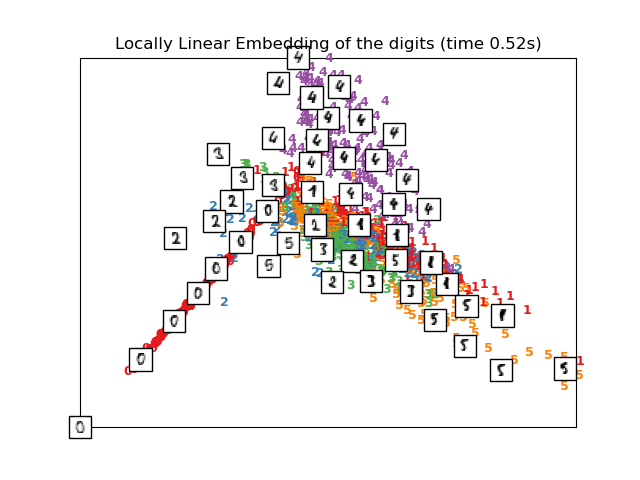
2.2.3.1. Complejidad¶
El algoritmo ELL estándar comprende tres etapas:
Búsqueda de vecinos más cercanos. Ver la discusión bajo Isomap más arriba.
Construcción de la matriz de ponderaciones. \(O[D N k^3]\). La construcción de la matriz de ponderaciones ELL involucra la solución de una ecuación lineal \(k \times k\) para cada uno de los \(N\) vecindarios locales
Decomposición de Autovalores Parcial. Ver la discusión bajo Isomap más arriba.
La complejidad general del ELL estándar es \(O[D \log(k) N \log(N)] + O[D N k^3] + O[d N^2]\).
\(N\) : número de puntos de datos de entrenamiento
\(D\): dimensión de entrada
\(k\) : número de vecinos más cercanos
\(d\): dimensión de salida
Referencias:
«Nonlinear dimensionality reduction by locally linear embedding» Roweis, S. & Saul, L. Science 290:2323 (2000)
2.2.4. Embedding modificado localmente lineal¶
Un problema bastante bien conocido con ELL es el problema de regularización. Cuando el número de vecinos es mayor que el número de dimensiones de entrada, la matriz que define cada vecindario local es deficiente de rango. Para abordar esto, el ELL estándar aplica un parámetro de regularización arbitraria \(r\), que se escoge en función del trazo de la matriz de ponderaciones local. Aunque puede comprobarse formalmente que cuando \(r \to 0\), la solución converge al embedding buscado, no hay garantía de que la solución óptima se encontrará para \(r > 0\). Este problema se manifiesta en embeddings que distorsionan la geometría subyacente del colector.
Un método para abordar el problema de regularización es usar múltiples vectores de ponderaciones en cada vecindario. Esta es la esencia del embedding modíficado localmente lineal (EMLL). El EMLL puede ser utilizado con la función locally_linear_embedding, y también su contraparte orientada a objetos LocallyLinearEmbedding, con la palabra clave method = 'modified'. Requiere que n_neighbors > n_components.
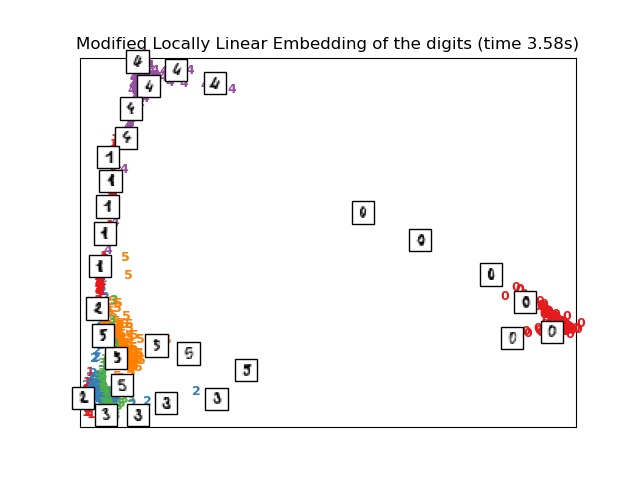
2.2.4.1. Complejidad¶
El algoritmo EMLL comprende tres etapas:
Búsqueda de vecinos más cercanos. Igual que el ELL estándar
Construcción de matríz de ponderados. Aproximadamente \(O[D N k^3] + O[N (k-D) k^2]\). El primer termino es exactamente equivalente a aquél del ELL estándar. El segundo termino tiene que ver con la construcción de la matriz de ponderados desde multiples ponderados. En la practica, el costo añadido de construir la matriz de ponderados EMLL es relativamente pequeña comparada al costo de las etapas 1 y 3.
Decomposición de Autovalores Parcial. Igual que el ELL estándar
La complejidad general del EMLL es \(O[D \log(k) N \log(N)] + O[D N k^3] + O[N (k-D) k^2] + O[d N^2]\).
\(N\) : número de puntos de datos de entrenamiento
\(D\): dimensión de entrada
\(k\) : número de vecinos más cercanos
\(d\): dimensión de salida
Referencias:
«MLLE: Modified Locally Linear Embedding Using Multiple Weights» Zhang, Z. & Wang, J.
2.2.5. Eigenmapeo Hessiano¶
El Eigenmapeo Hessiano (también conocido como ELL basado en Hessians: ELLH) es otro método para resolver el problema de regularización del ELL. Gira en torno a una forma cuadrática basada en hessianos en cada vecindario que es usada para recuperar la estructura localmente lineal. Aunque otras implementaciones señalan su mal escalamiento con el tamaño de los datos, sklearn implementa algunas mejoras algorítmicas que hacen que su costo sea comparable a aquel de otras variantes ELL para dimensiones de salida pequeñas. Se puede realizar el ELLH con la función locally_linear_embedding o su contraparte orientada a objetos LocallyLinearEmbedding, con la palabra clave method = 'hessian'. Requiere que n_neighbors > n_components * (n_components + 3) / 2.
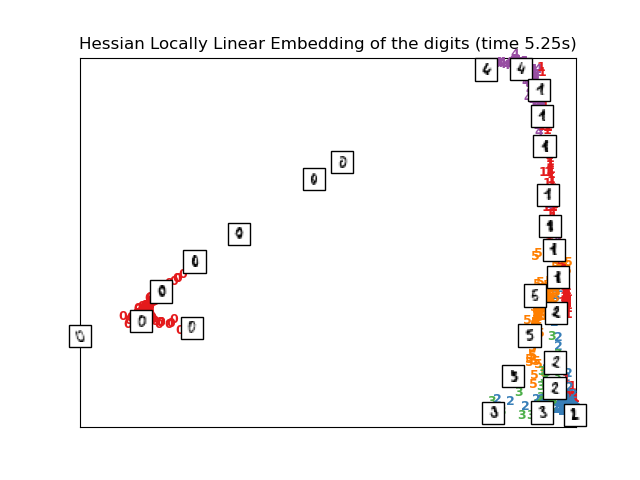
2.2.5.1. Complejidad¶
El algoritmo ELLH comprende tres etapas:
Búsqueda de vecinos más cercanos. Igual que el ELL estándar
Construcción de la Matriz de Ponderado. Aproximadamente \(O[D N k^3] + O[N d^6]\). El primer término refleja un costo similar a aquel del ELL estándar. El segundo término viene de una descomposición QR del estimador local de hessianos.
Decomposición de Autovalores Parcial. Igual que el ELL estándar
La complejidad general del ELLH estándar es \(O[D \log(k) N \log(N)] + O[D N k^3] + O[N d^6] + O[d N^2]\).
\(N\) : número de puntos de datos de entrenamiento
\(D\): dimensión de entrada
\(k\) : número de vecinos más cercanos
\(d\): dimensión de salida
Referencias:
«Hessian Eigenmaps: Locally linear embedding techniques for high-dimensional data» Donoho, D. & Grimes, C. Proc Natl Acad Sci USA. 100:5591 (2003)
2.2.6. Embedding Espectral¶
El Embedding Espectral es un acercamiento al calculo de un embedding no lineal. Scikit-learn implementa Eigenmaps Laplacianos, los cuales encuentran una representación de baja dimensión de los datos usando una descomposición espectral del Laplaciano del gráfico. El gráfico generado puede considerarse una aproximación discreta del colector de baja dimensión en el espacio de alta dimensión. La minimización de una función de costo basada en el gráfico asegura que los puntos cercanos en el colector son mapeados cerca uno de los otros en el espacio de baja dimensión, preservando distancias locales. El Embedding Espectral puede realizarse con la función spectral_embedding o con su contraparte orientada a objetos SpectralEmbedding.
2.2.6.1. Complejidad¶
El algoritmo de Embedding Espectral (Eigenmaps Laplacianos) comprende tres etapas:
Construcción de gráfico ponderado. Transforma los datos de entrada en bruto en una representación gráfica usando una representación de matriz por afinidad (adyacencia).
Construcción del Grafo Laplaciano. El grafo Laplaciano sin normalizar se construye como \(L = D - A\) y el normalizado se construye como \(L = D^{-\frac{1}{2}} (D - A) D^{-\frac{1}{2}}\).
Decomposición parcial de Autovalor. La descomposición del autovalor se realiza en el grafo Laplaciano
La complejidad general del embedding espectral es \(O[D \log(k) N \log(N)] + O[D N k^3] + O[d N^2]\).
\(N\) : número de puntos de datos de entrenamiento
\(D\): dimensión de entrada
\(k\) : número de vecinos más cercanos
\(d\): dimensión de salida
Referencias:
«Laplacian Eigenmaps for Dimensionality Reduction and Data Representation» M. Belkin, P. Niyogi, Neural Computation, June 2003; 15 (6):1373-1396
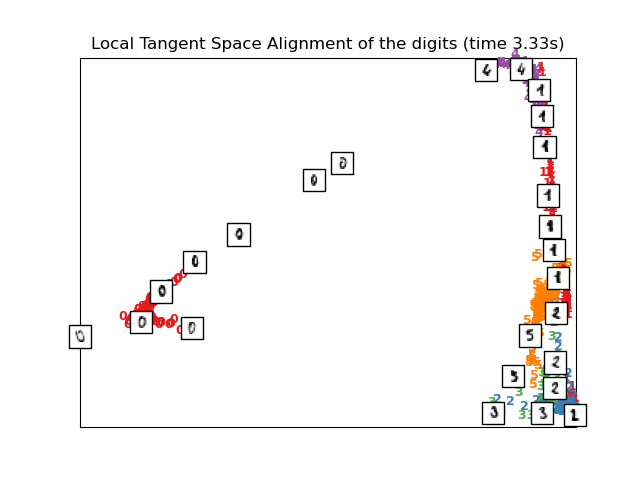
2.2.7. Alineación del Espacio Tangente Local¶
Aunque técnicamente no sea una variante del ELL, el alineamiento del espacio tangente local (AETL, o LTSA en inglés) es lo suficientemente similar algorítmicamente al ELL que se puede poner en esta categoría. En lugar de enfocarse en preservar distancias del vecindario como en el ELL, el AETL busca caracterizar la geometría local en cada vecindario mediante su espacio tangente, y realiza una optimización global para alinear estos espacios locales tangentes y así aprender el embedding. El AETL puede realizarse con la función locally_linear_embedding o su contraparte orientada a objetos LocallyLinearEmbedding, con la palabra clave method = 'ltsa'.
2.2.7.1. Complejidad¶
El algoritmo LTSA comprende tres etapas:
Búsqueda de vecinos más cercanos. Igual que el ELL estándar
Construcción de la matriz de ponderaciónes. Aproximadamente \(O[D N k^3] + O[k^2 d]\). El primer termino refleja un costo similar al de LLE estándar.
Decomposición de Autovalores Parcial. Igual que el ELL estándar
La complejidad general del LTSA estándar es \(O[D \log(k) N \log(N)] + O[D N k^3] + O[k^2 d] + O[d N^2]\).
\(N\) : número de puntos de datos de entrenamiento
\(D\): dimensión de entrada
\(k\) : número de vecinos más cercanos
\(d\): dimensión de salida
Referencias:
«Principal manifolds and nonlinear dimensionality reduction via tangent space alignment» Zhang, Z. & Zha, H. Journal of Shanghai Univ. 8:406 (2004)
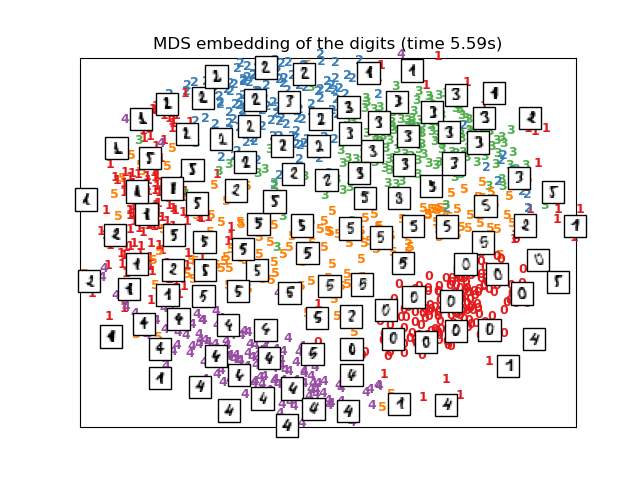
2.2.8. Escalamiento Multidimensional (Multi-dimensional Scaling, MDS)¶
Escalamiento multidimensional (MDS) busca una representación de baja dimensión de los datos en la que las distancias respeten bien las distancias en el espacio original de alta dimensión.
En general, MDS es una técnica utilizada para analizar datos de similitud o disimilitud. Intenta modelar la similitud o disimilitud de los datos como distancias en espacios geométricos. Los datos pueden ser calificaciones de similitud entre objetos, frecuencias de interacción de moléculas, o índices de comercio entre países.
Existen dos tipos de algoritmos MDS (escalamiento multidimensional): métrico y no métrico. En scikit-learn, la clase MDS implementa ambos. En el MDS métrico, la matriz de similitud de entrada viene de una métrica (y por tanto respeta la desigualdad triangular), las distancias entre dos puntos de salida son entonces establecidas para ser tan cercanas como es posible a los datos de similitud o disimilitud. En la versión no métrica, los algoritmos intentarán preservar el orden de las distancias y, por tanto, buscarán una relación monótona entre las distancias en el espacio con embedding y las similitudes/disimilitudes.
Sea \(S\) la matriz de similitud, y \(X\) las coordenadas de los \(n\) puntos de entrada. La disparidades \(\hat{d}_{ij}\) son transformaciones de las similitudes escogidas en ciertas maneras óptimas. El objetivo, llamado el estrés, entonces es definido por \(\sum_{i < j} d_{ij}(X) - \hat{d}_{ij}(X)\)
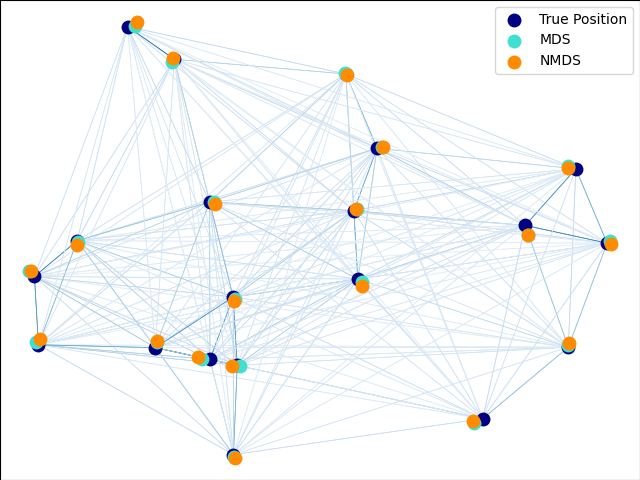
2.2.8.1. MDS (Escalamiento multidimensional) Métrico¶
En el modelo MDS métrico más simple, llamado MDS absoluto, las disparidades son definidas por \(\hat{d}_{ij} = S_{ij}\). Con el MDS absoluto, el valor \(S_{ij}\) debería entonces corresponder exactamente a la distancia entre el punto \(i\) y \(j\) en el punto de embedding.
Más comúnmente, las disparidades se establecen como \(\hat{d}_{ij} = b S_{ij}\).
2.2.8.2. MDS (Escalamiento Multidimensional) no métrico¶
El MDS no métrico se enfoca en la ordenación de los datos. Si \(S_{ij} < S_{jk}\), entonces el embedding debería imponer \(d_{ij} < d_{jk}\). Un algoritmo simple para imponerlo es el uso de una regresión monótona de \(d_{ij}\) en \(S_{ij}\), produciendo las disparidades \(\hat{d}_{ij}\) en el mismo orden que \(S_{ij}\).
Una solución trivial a este problema es establecer todos los puntos en el origen. Para evitar eso, las disparidades \(\hat{d}_{ij}\) son normalizadas.
Referencias:
«Modern Multidimensional Scaling - Theory and Applications» Borg, I.; Groenen P. Springer Series in Statistics (1997)
«Nonmetric multidimensional scaling: a numerical method» Kruskal, J. Psychometrika, 29 (1964)
«Multidimensional scaling by optimizing goodness of fit to a nonmetric hypothesis» Kruskal, J. Psychometrika, 29, (1964)
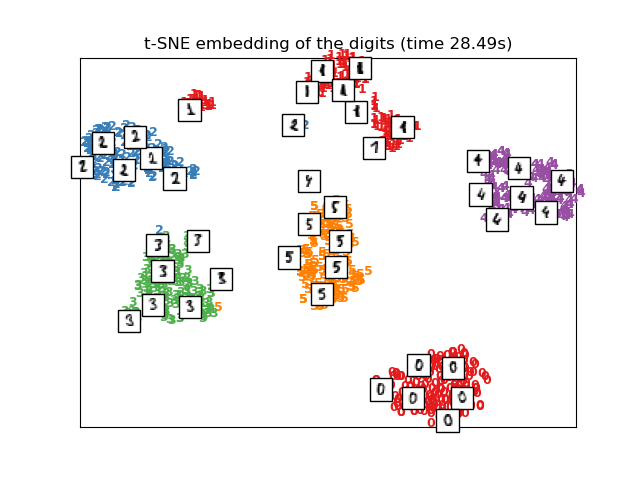
2.2.9. Embedding Estocástico de Vecinos distribuido t (t-distributed Stochastic Neighbor Embedding, t-SNE)¶
t-SNE (TSNE) convierte las afinidades de puntos de datos a probabilidades. Las afinidades en el espacio original están representadas por probabilidades conjuntas Gaussianas y las afinidades en el espacio con embedding son representadas por las distribuciones t de Student. Esto permite que t-SNE sea particularmente sensible a la estructura local y tiene algunas otras ventajas sobre las técnicas existentes:
Revelación de la estructura en muchas escalas en un solo mapa
Revelación de datos que se encuentran en múltiples, diferentes, variedades o conglomerados
Reducir la tendencia a acumular los puntos juntos en el centro
Mientras que Isomap, LLE y sus variantes son más adecuadas para desplegar una única variedad continua de dimensionalidad baja, el t-SNE se enfocará en la estructura local de los datos y va a tender a extraer grupos locales de muestras agrupadas como se resalta en el ejemplo de la curva S. Esta habilidad de agrupar muestras basadas en la estructura local quizás sea beneficiosa para desenredar visualmente un conjunto de datos que compromete múltiples variedades al mismo tiempo como es el caso en el conjunto de datos digits.
La divergencia Kullback-Leibler (KL) de las probabilidades conjuntas en el espacio original y en el espacio con embedding será minimizada por descenso del gradiente. Ten en cuenta que la divergencia KL no es convexa, es decir, múltiples reinicios con inicializaciones distintas van a terminar en los mínimos locales de la divergencia KL. Por lo tanto, a veces es útil utilizar diferentes semillas y seleccionar el embedding con la menor divergencia KL.
Las desventajas de usar t-SNE son aproximadamente:
el t-SNE es computacionalmente costoso, y puede tomar varias horas en conjuntos de datos con millones de muestras, mientras que el PCA termina en segundos o minutos
El método Barnes-Hut t-SNE está limitado a embeddings de dos o tres dimensiones.
El algoritmo es estocástico y varios reinicios con diferentes semillas pueden producir embeddings distintos. Sin embargo, es perfectamente legítimo elegir el embedding con el menor error.
La estructura global no se preserva explícitamente. Este problema se puede mitigar inicializando puntos con PCA, análisis de componentes principales, (utilizando
init='pca').
2.2.9.1. Optimización de t-SNE¶
El principal objetivo de t-SNE es la visualización de datos de alta dimensión. Por lo tanto, funciona mejor cuando a los datos se les aplica un embedding en dos o tres dimensiones.
Optimizar la divergencia KL puede ser un poco complicado a veces. Hay 5 parámetros que controlan la optimización del t-SNE y, por tanto, posiblemente la calidad del embedding resultante:
perplejidad
factor de exageración temprana
tasa de aprendizaje
número máximo de iteraciones
ángulo (no usado en el método exacto)
La perplejidad está definida como \(k=2^{(S)}\) donde \(S\) es la entropía de Shannon de la distribución de probabilidad condicional. La perplejidad de un dado de \(k\) lados es \(k\), por lo que \(k\) es efectivamente el número de vecinos más cercanos que considera t-SNE cuando genera las probabilidades condicionales. Las perplejidades más grandes conducen a más vecinos cercanos y menor sensibilidad a estructuras pequeñas. Por el contrario, una perplejidad menor considera un número pequeño de vecinos, y por tanto, ignora más información global a favor del vecindario local. Mientras los conjuntos de datos sean más grandes, más puntos serán requeridos para obtener una muestra razonable del vecindario local, y por lo tanto, pueden requerirse perplejidades más grandes. Similarmente, conjuntos de datos con más ruido van a requerir valores de perplejidad más grandes para abarcar suficientes vecinos locales para ver más allá del ruido de fondo.
El número máximo de iteraciones suele ser lo suficientemente alto y no requiere ningún ajuste. La optimización consta de dos fases: la fase de exageración temprana y la última optimización. Durante la exageración temprana las probabilidades conjuntas en el espacio original serán incrementadas artificialmente mediante la multiplicación con un factor dado. Los factores más grandes resultan en brechas más grandes entre los conglomerados naturales en los datos. Si el factor es demasiado grande, la divergencia KL podría incrementar en esta fase. Normalmente no requiere ser ajustado. Un parámetro crítico es la tasa de aprendizaje. Si es demasiado baja, el descenso del gradiente se atascará en un mínimo local malo. Si es demasiado alta, la divergencia KL incrementará durante la optimización. Puedes encontrar más consejos en el FAQ de Laurens van der Maaten (ver referencias). El último parámetro, el ángulo, es un intercambio entre el rendimiento y la exactitud. Ángulos más grandes implican que podemos aproximar regiones más grandes con un solo punto, lo que lleva a una mejor velocidad pero a resultados menos exactos.
«How to Use t-SNE Effectively» proporciona una buena discusión de los efectos de los diferentes parámetros, así como gráficos interactivos para explorar los efectos de diferentes parámetros.
2.2.9.2. Barnes-Hut t-SNE¶
El Barnes-Hut t-SNE que se ha implementado aquí es normalmente mucho más lento que otros algoritmos de aprendizaje múltiple. La optimización es bastante difícil y el cálculo del gradiente es \(O[d N log(N)]\), donde \(d\) es el número de dimensiones de salida y \(N\) es el número de muestras. El método de Barnes-Hut mejora en el método exacto donde la complejidad t-SNE es \(O[d N^2]\), pero tiene otras diferencias notables:
La implementación de Barnes-Hut solo funciona cuando la dimensionalidad del objetivo es 3 o menos. El caso 2D es típico cuando se construyen visualizaciones.
Barnes-Hut solo funciona con datos de entrada densos. A las matrices de datos dispersas solo se les puede realizar embedding con el método exacto o pueden ser aproximadas por una proyección de bajo rango densa, por ejemplo usando
TruncatedSVDBarnes-Hut es una aproximación del método exacto. La aproximación se parametriza con el parámetro angle, por lo tanto el parámetro angle no se utiliza cuando method=»exact»
Barnes-Hut es significativamente más escalable. Barnes-Hut puede ser usado para realizar embedding en cientos de miles de puntos de datos, mientras que el método exacto solo puede manejar miles de muestras antes de volverse inmanejable computacionalmente
Para fines de visualización (que es el principal caso de uso de t-SNE), se recomienda encarecidamente utilizar el método de Barnes-Hut. El método exacto t-SNE es útil para comprobar las propiedades teóricas del embedding, posiblemente en espacio de alta dimensionalidad pero limitado a conjuntos de datos pequeños debido a restricciones computacionales.
También ten en cuenta que las etiquetas de los dígitos más o menos corresponden al agrupamiento natural encontrado por t-SNE mientras que la proyección 2D lineal del modelo PCA da una representación donde gran parte de las regiones de etiqueta se superponen. Esta es una pista importante de que estos datos pueden ser bien separados por métodos no lineales que se enfocan en la estructura local (por ejemplo, un SVM con un kernel RBF Gaussiano). Sin embargo, no visualizar grupos bien separados etiquetados de forma homogénea con t-SNE en 2D no implica necesariamente que los datos no pueden ser clasificados correctamente por un modelo supervisado. Podría darse el caso de que 2 dimensiones no sean lo suficientemente bajas como para representar con exactitud la estructura interna de los datos.
Referencias:
«Visualizing High-Dimensional Data Using t-SNE» van der Maaten, L.J.P.; Hinton, G. Journal of Machine Learning Research (2008)
«t-Distributed Stochastic Neighbor Embedding» van der Maaten, L.J.P.
«Accelerating t-SNE using Tree-Based Algorithms.» L.J.P. van der Maaten. Journal of Machine Learning Research 15(Oct):3221-3245, 2014.
2.2.10. Consejos sobre el uso práctico¶
Asegúrate de que se utiliza la misma escala en toda las características. Debido a que los métodos de aprendizaje múltiple están basados en una búsqueda del vecino más cercano, el algoritmo podría tener un rendimiento deficiente si no es así. Ver StandardScaler para conocer formas convenientes de escalar datos heterogéneos.
El error de reconstrucción calculado por cada rutina se puede utilizar para escoger la dimensión de salida óptima. Para una variedad \(d\)-dimensional incrustada en un espacio de parámetros \(D\)-dimensional, el error de reconstrucción disminuirá a medida que
n_componentsse incremente hasta quen_components == d.Ten en cuenta que los datos ruidosos pueden hacerle un «cortocircuito» a la variedad, en esencia actuando como un puente entre partes de la variedad que de otro modo estarían bien separadas. El aprendizaje múltiple en datos incompletos o ruidosos es una área activa de investigación.
Algunas configuraciones de entrada pueden dar lugar a matrices de ponderación singulares, por ejemplo, cuando más de dos puntos del conjunto de datos son idénticos, o cuando los datos están divididos en grupos disjuntos. En este caso,
solver='arpack'no podrá encontrar el espacio nulo. La forma más sencilla de solucionar esto es utilizarsolver='dense'que funcionará en una matriz singular, aunque quizás sea muy lento dependiendo del número de puntos de entrada. Alternativamente, se puede intentar comprender el origen de la singularidad: si se debe a conjuntos disjuntos, aumentarn_neighborspuede ayudar. Si se debe a puntos idénticos en el conjunto de datos, eliminar estos puntos puede ayudar.
Ver también
Incrustación de Arboles Totalmente Aleatorios también puede ser útil para derivar representaciones no lineales del espacio de características, y no realiza una reducción de dimensionalidad.