6.3. Preprocesamiento de los datos¶
El paquete sklearn.preprocessing proporciona varias funciones de utilidad comunes y clases transformadoras para cambiar los vectores de características en bruto a una representación que sea más adecuada para los estimadores posteriores.
En general, los algoritmos de aprendizaje se benefician de la estandarización del conjunto de datos. Si hay algunos valores atípicos presentes en el conjunto, los escaladores robustos o transformadores son más apropiados. Los comportamientos de los diferentes escaladores, transformadores y normalizadores en un conjunto de datos que contiene valores atípicos marginales se resaltan en Compara el efecto de los diferentes escaladores en los datos con los atípicos.
6.3.1. Estandarización, o eliminación media y escala de varianza¶
La Estandarización de conjuntos de datos es un requisito común para muchos estimadores de aprendizaje automático implementados en scikit-learn; podrían comportarse mal si las características individuales no se ven más o menos como datos distribuidos normalmente estándar: Gaussiana con media cero y varianza unitaria.
En la práctica a menudo ignoramos la forma de la distribución y simplemente transformamos los datos para centrarlos eliminando el valor medio de cada característica, luego los escalamos dividiendo características no constantes por su desviación estándar.
Por ejemplo, muchos elementos utilizados en la función objetivo de un algoritmo de aprendizaje (como el kernel RBF de Máquinas de Vectores de Soporte o los regularizadores l1 y l2 de modelos lineales) asumen que todas las características están centradas en cero y tienen varianza del mismo orden. Si una característica tiene varianza de un orden de magnitud mayor que otras, podría dominar la función objetivo y hacer que el estimador no pueda aprender de otras características correctamente como se esperaba.
El módulo preprocessing proporciona la clase de utilidad StandardScaler, que es una forma rápida y sencilla de realizar la siguiente operación en un conjunto de datos array-like:
>>> from sklearn import preprocessing
>>> import numpy as np
>>> X_train = np.array([[ 1., -1., 2.],
... [ 2., 0., 0.],
... [ 0., 1., -1.]])
>>> scaler = preprocessing.StandardScaler().fit(X_train)
>>> scaler
StandardScaler()
>>> scaler.mean_
array([1. ..., 0. ..., 0.33...])
>>> scaler.scale_
array([0.81..., 0.81..., 1.24...])
>>> X_scaled = scaler.transform(X_train)
>>> X_scaled
array([[ 0. ..., -1.22..., 1.33...],
[ 1.22..., 0. ..., -0.26...],
[-1.22..., 1.22..., -1.06...]])
Los datos escalados tienen una media cero y varianza unitaria:
>>> X_scaled.mean(axis=0)
array([0., 0., 0.])
>>> X_scaled.std(axis=0)
array([1., 1., 1.])
Esta clase implementa la API Transformer para calcular la media y la desviación estándar en un conjunto de entrenamiento para poder volver a aplicar posteriormente la misma transformación en el conjunto de prueba. Esta clase es, por lo tanto, adecuada para su uso en los primeros pasos de un Pipeline:
>>> from sklearn.datasets import make_classification
>>> from sklearn.linear_model import LogisticRegression
>>> from sklearn.model_selection import train_test_split
>>> from sklearn.pipeline import make_pipeline
>>> from sklearn.preprocessing import StandardScaler
>>> X, y = make_classification(random_state=42)
>>> X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
>>> pipe = make_pipeline(StandardScaler(), LogisticRegression())
>>> pipe.fit(X_train, y_train) # apply scaling on training data
Pipeline(steps=[('standardscaler', StandardScaler()),
('logisticregression', LogisticRegression())])
>>> pipe.score(X_test, y_test) # apply scaling on testing data, without leaking training data.
0.96
Es posible desactivar el centrado o el escalado pasando with_mean=False o with_std=False al constructor de StandardScaler.
6.3.1.1. Escalamiento de las características a un rango¶
Una estandarización alternativa es el escalamiento de características para que se sitúen entre un valor mínimo y máximo determinado, a menudo entre cero y uno, o para que el valor absoluto máximo de cada característica se escalado al tamaño unitario. Esto puede lograrse utilizando MinMaxScaler o MaxAbsScaler, respectivamente.
La motivación para utilizar esta escala incluye robustez ante desviaciones estándar muy pequeñas de las características y preservando las entradas cero en los datos dispersos.
Aquí hay un ejemplo para escalar una matriz de datos de juguete al rango [0, 1]:
>>> X_train = np.array([[ 1., -1., 2.],
... [ 2., 0., 0.],
... [ 0., 1., -1.]])
...
>>> min_max_scaler = preprocessing.MinMaxScaler()
>>> X_train_minmax = min_max_scaler.fit_transform(X_train)
>>> X_train_minmax
array([[0.5 , 0. , 1. ],
[1. , 0.5 , 0.33333333],
[0. , 1. , 0. ]])
La misma instancia del transformador puede aplicarse a unos nuevos datos de prueba no vistos durante el llamado de ajuste: se aplicarán las mismas operaciones de escalamiento y desplazamiento para ser coherentes con la transformación realizada en los datos de entrenamiento:
>>> X_test = np.array([[-3., -1., 4.]])
>>> X_test_minmax = min_max_scaler.transform(X_test)
>>> X_test_minmax
array([[-1.5 , 0. , 1.66666667]])
Es posible inspeccionar los atributos del escalador para encontrar la naturaleza exacta de la transformación aprendida en los datos de entrenamiento:
>>> min_max_scaler.scale_
array([0.5 , 0.5 , 0.33...])
>>> min_max_scaler.min_
array([0. , 0.5 , 0.33...])
Si a MinMaxScaler se le da un feature_range=(min, max) explícito la fórmula completa es:
X_std = (X - X.min(axis=0)) / (X.max(axis=0) - X.min(axis=0))
X_scaled = X_std * (max - min) + min
MaxAbsScaler funciona de una manera muy similar, pero escala de una manera que los datos de entrenamiento se encuentran dentro del rango [-1, 1] dividiendo entre el valor máximo más grande en cada característica. Está pensado para datos que ya están centrados en cero o datos dispersos.
Aquí está cómo utilizar los datos de juguete del ejemplo anterior con este escalador:
>>> X_train = np.array([[ 1., -1., 2.],
... [ 2., 0., 0.],
... [ 0., 1., -1.]])
...
>>> max_abs_scaler = preprocessing.MaxAbsScaler()
>>> X_train_maxabs = max_abs_scaler.fit_transform(X_train)
>>> X_train_maxabs
array([[ 0.5, -1. , 1. ],
[ 1. , 0. , 0. ],
[ 0. , 1. , -0.5]])
>>> X_test = np.array([[ -3., -1., 4.]])
>>> X_test_maxabs = max_abs_scaler.transform(X_test)
>>> X_test_maxabs
array([[-1.5, -1. , 2. ]])
>>> max_abs_scaler.scale_
array([2., 1., 2.])
6.3.1.2. Escalamiento de datos dispersos¶
Centrar datos dispersos destruiría la estructura de dispersión en los datos, por lo que rara vez es algo sensato para hacer. Sin embargo, puede tener sentido escalar las entradas dispersas, especialmente si las características están en diferentes escalas.
MaxAbsScaler fue diseñado específicamente para el escalamiento de datos dispersos, y es la forma recomendada de hacerlo. Sin embargo, StandardScaler puede aceptar matrices scipy.sparse como entrada, siempre que se pase explícitamente with_mean=False al constructor. De lo contrario, se producirá un ValueError ya que el centrado silencioso rompería la dispersión y a menudo bloquearía la ejecución al asignar involuntariamente cantidades excesivas de memoria. RobustScaler no puede ajustarse a entradas dispersas, pero puede utilizar el método transform en entradas dispersas.
Ten en cuenta que los escaladores aceptan tanto el formato de Filas Dispersas Comprimidas (CSR) como el formato de Columnas Dispersas Comprimidas (CSC) (ver scipy.sparse.csr_matrix y scipy.sparse.csc_matrix). Cualquier otra entrada dispersa será convertida a la representación Filas Dispersas Comprimidas. Para evitar copias de memoria innecesarias, se recomienda elegir la representación CSR o CSC en la parte superior.
Por último, si se espera que los datos centrados sean lo suficientemente pequeños, otra opción es convertir explícitamente la entrada en un arreglo utilizando el método toarray de matrices dispersas.
6.3.1.3. Escalamiento de datos con valores atípicos¶
Si tus datos contienen muchos valores atípicos, es probable que el escalamiento utilizando la media y la varianza de los datos no funcione muy bien. En estos casos, puedes utilizar RobustScaler como reemplazo. Este utiliza estimaciones más robustas para el centrado y el rango de tus datos.
Referencias:
Más información sobre la importancia del centrado y escalamiento de los datos está disponible en este FAQ:Should I normalize/standardize/rescale the data?
Escalamiento vs Whitening
A veces no es suficiente con centrar y escalar las características de forma independiente, ya que un modelo posterior puede hacer alguna suposición sobre la independencia lineal de las características.
Para solucionar este problema se puede utilizar PCA con whiten=True para eliminar aún más la correlación lineal entre las características.
6.3.1.4. Centrado de matrices del núcleo¶
Si tienes una matriz de núcleo de un núcleo \(K\) que calcula un producto punto en un espacio de características definido por la función \(\phi\), un KernelCenterer puede transformar la matriz de núcleo para que contenga productos internos en el espacio de características definido por \(\phi\) seguido de la eliminación de la media en ese espacio.
6.3.2. Transformación no lineal¶
Hay dos tipos de transformaciones disponibles: las transformaciones de cuantiles y las transformaciones de potencia. Tanto las transformaciones de cuantiles como las de potencia se basan en transformaciones monótonas de las características y, por tanto, preservan el rango de los valores a lo largo de cada característica.
Las transformaciones de cuantiles ponen todas las características en la misma distribución deseada basándose en la fórmula \(G^{-1}(F(X))\) donde \(F\) es la función de distribución acumulada de la característica y \(G^{-1}\) la función cuantil de la distribución de salida deseada \(G\). Esta fórmula utiliza los dos siguientes hechos: (i) si \(X\) es una variable aleatoria con una función de distribución acumulada continua \(F\), entonces \(F(X)\) se distribuye uniformemente en \([0, 1]\); (ii) si \(U\) es una variable aleatoria con distribución uniforme en \([0, 1]\) entonces \(G^{-1}(U)\) tiene distribución \(G\). Al realizar una transformación de rango, una transformación de cuantil suaviza las distribuciones inusuales y está menos influenciada por los valores atípicos que los métodos de escalamiento. Sin embargo, distorsiona las correlaciones y distancias dentro y entre características.
Las transformaciones de potencia son una familia de transformaciones paramétricas cuyo objetivo es mapear datos de cualquier distribución a lo más parecido a una Distribución Gaussiana.
6.3.2.1. Mapeo a una Distribución Uniforme¶
QuantileTransformer proporciona una transformación no paramétrica para mapear los datos a una distribución uniforme con valores entre 0 y 1:
>>> from sklearn.datasets import load_iris
>>> from sklearn.model_selection import train_test_split
>>> X, y = load_iris(return_X_y=True)
>>> X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
>>> quantile_transformer = preprocessing.QuantileTransformer(random_state=0)
>>> X_train_trans = quantile_transformer.fit_transform(X_train)
>>> X_test_trans = quantile_transformer.transform(X_test)
>>> np.percentile(X_train[:, 0], [0, 25, 50, 75, 100])
array([ 4.3, 5.1, 5.8, 6.5, 7.9])
Esta característica corresponde a la longitud del sépalo en cm. Una vez aplicada la transformación de cuantiles, esos hitos se acercan estrechamente a los percentiles definidos anteriormente:
>>> np.percentile(X_train_trans[:, 0], [0, 25, 50, 75, 100])
...
array([ 0.00... , 0.24..., 0.49..., 0.73..., 0.99... ])
Esto puede confirmarse en un conjunto de pruebas independientes con observaciones similares:
>>> np.percentile(X_test[:, 0], [0, 25, 50, 75, 100])
...
array([ 4.4 , 5.125, 5.75 , 6.175, 7.3 ])
>>> np.percentile(X_test_trans[:, 0], [0, 25, 50, 75, 100])
...
array([ 0.01..., 0.25..., 0.46..., 0.60... , 0.94...])
6.3.2.2. Mapeo a una Distribución Gaussiana¶
En muchos escenarios de modelado, es deseable la normalidad de las características de un conjunto de datos. Las transformaciones de potencia son una familia de transformaciones paramétricas y monótonas cuyo objetivo es mapear los datos de cualquier distribución a una distribución lo más cercana posible a una distribución Gaussiana con el fin de estabilizar la varianza y minimizar la asimetría.
PowerTransformer actualmente proporciona dos transformaciones de potencia de este tipo, la transformación Yeo-Johnson y la transformación Box-Cox.
La transformación Yeo-Johnson viene dada por:
mientras que la transformación Box-Cox viene dada por:
Box-Cox sólo puede aplicarse a datos estrictamente positivos. En ambos métodos, la transformación está parametrizada por \(\lambda\), que se determina a través de la estimación de máxima verosimilitud. Aquí hay un ejemplo de uso de Box-Cox para mapear muestras extraídas de una distribución lognormal a una distribución normal:
>>> pt = preprocessing.PowerTransformer(method='box-cox', standardize=False)
>>> X_lognormal = np.random.RandomState(616).lognormal(size=(3, 3))
>>> X_lognormal
array([[1.28..., 1.18..., 0.84...],
[0.94..., 1.60..., 0.38...],
[1.35..., 0.21..., 1.09...]])
>>> pt.fit_transform(X_lognormal)
array([[ 0.49..., 0.17..., -0.15...],
[-0.05..., 0.58..., -0.57...],
[ 0.69..., -0.84..., 0.10...]])
Mientras que el ejemplo anterior establece la opción standardize en False, PowerTransformer aplicará por defecto una normalización de media cero y varianza unitaria a la salida transformada.
A continuación se muestran ejemplos de Box-Cox y Yeo-Johnson aplicados a varias distribuciones de probabilidad. Ten en cuenta que cuando se aplican a ciertas distribuciones, las transformaciones de potencia consiguen resultados muy parecidos a los Gaussianos, pero con otras, son ineficaces. Esto resalta la importancia de visualizar los datos antes y después de la transformación.
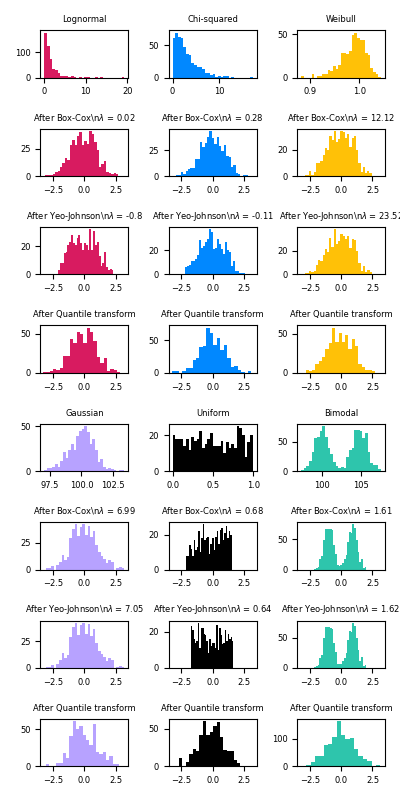
También es posible mapear los datos a una distribución normal usando QuantileTransformer estableciendo output_distribution='normal'. Utilizando el ejemplo anterior con el conjunto de datos iris:
>>> quantile_transformer = preprocessing.QuantileTransformer(
... output_distribution='normal', random_state=0)
>>> X_trans = quantile_transformer.fit_transform(X)
>>> quantile_transformer.quantiles_
array([[4.3, 2. , 1. , 0.1],
[4.4, 2.2, 1.1, 0.1],
[4.4, 2.2, 1.2, 0.1],
...,
[7.7, 4.1, 6.7, 2.5],
[7.7, 4.2, 6.7, 2.5],
[7.9, 4.4, 6.9, 2.5]])
Así, la mediana de la entrada se convierte en la media de la salida, centrada en 0. La salida normal es recortada para que el mínimo y el máximo de la entrada — correspondientes a las cantidades 1e-7 y 1 - 1e-7 respectivamente — no se conviertan en infinitos bajo la transformación.
6.3.3. Normalización¶
La normalización es el proceso de escalamiento de muestras individuales para tener la norma unitaria. Este proceso puede ser útil si planeas utilizar una forma cuadrática como el producto punto o cualquier otro núcleo para cuantificar la similitud de cualquier par de muestras.
Este supuesto es la base del Modelo de espacio vectorial utilizado a menudo en los contextos de clasificación y agrupamiento de textos.
La función normalize proporciona una forma rápida y sencilla de realizar esta operación en un único conjunto de datos array-like, ya sea utilizando las normas l1, l2 o max:
>>> X = [[ 1., -1., 2.],
... [ 2., 0., 0.],
... [ 0., 1., -1.]]
>>> X_normalized = preprocessing.normalize(X, norm='l2')
>>> X_normalized
array([[ 0.40..., -0.40..., 0.81...],
[ 1. ..., 0. ..., 0. ...],
[ 0. ..., 0.70..., -0.70...]])
El módulo preprocessing proporciona además una clase de utilidad Normalizer que implementa la misma operación utilizando la API Transformer (aunque el método fit es inútil en este caso: la clase no tiene estado ya que esta operación trata las muestras de forma independiente).
Esta clase es, por tanto, adecuada para su uso en los primeros pasos de un Pipeline:
>>> normalizer = preprocessing.Normalizer().fit(X) # fit does nothing
>>> normalizer
Normalizer()
La instancia del normalizador puede utilizarse en vectores de muestra como cualquier transformador:
>>> normalizer.transform(X)
array([[ 0.40..., -0.40..., 0.81...],
[ 1. ..., 0. ..., 0. ...],
[ 0. ..., 0.70..., -0.70...]])
>>> normalizer.transform([[-1., 1., 0.]])
array([[-0.70..., 0.70..., 0. ...]])
Nota: La normalización L2 también se conoce como preprocesamiento de signos espaciales.
Entrada dispersa
normalize and Normalizer aceptan tanto array-like densos como matrices dispersas de scipy.sparse como entrada.
Para la entrada dispersa los datos son **convertidos a la representación Filas Dispersas Comprimidas ** (ver scipy.sparse.csr_matrix) antes de ser alimentado a las rutinas eficientes de Cython. Para evitar copias de memoria innecesarias, se recomienda elegir la representación CSR de entrada.
6.3.4. Codificación de características categóricas¶
A menudo las características no se dan como valores continuos sino como categóricos. Por ejemplo, una persona podría tener características ["male", "female"],``[«from Europe», «from US», «from Asia»]``, ["uses Firefox", "uses Chrome", "uses Safari", "uses Internet Explorer"]. Estas características pueden codificarse eficazmente como enteros, por ejemplo ["male", "from US", "uses Internet Explorer"] podría expresarse como [0, 1, 3] mientras que ["female", "from Asia", "uses Chrome"] sería [1, 2, 1].
Para convertir características categóricas en dichos códigos de enteros, podemos utilizar el OrdinalEncoder. Este estimador transforma cada característica categórica en una nueva característica de enteros (0 a n_categorías - 1):
>>> enc = preprocessing.OrdinalEncoder()
>>> X = [['male', 'from US', 'uses Safari'], ['female', 'from Europe', 'uses Firefox']]
>>> enc.fit(X)
OrdinalEncoder()
>>> enc.transform([['female', 'from US', 'uses Safari']])
array([[0., 1., 1.]])
Sin embargo, esta representación de números enteros no puede utilizarse directamente con todos los estimadores de scikit-learn, ya que éstos esperan una entrada continua, e interpretarían las categorías como si estuvieran ordenadas, lo que a menudo no se desea (es decir, el conjunto de navegadores se ordenó arbitrariamente).
Otra posibilidad para convertir características categóricas en características que puedan ser utilizadas con los estimadores de scikit-learn es utilizar un one-of-K, también conocido como codificación one-hot o dummy. Este tipo de codificación se puede obtener con el OneHotEncoder, que transforma cada característica categórica con n_categories posibles en n_categories con características binarias, una de ellas 1, y todas las demás 0.
Continuando el ejemplo anterior:
>>> enc = preprocessing.OneHotEncoder()
>>> X = [['male', 'from US', 'uses Safari'], ['female', 'from Europe', 'uses Firefox']]
>>> enc.fit(X)
OneHotEncoder()
>>> enc.transform([['female', 'from US', 'uses Safari'],
... ['male', 'from Europe', 'uses Safari']]).toarray()
array([[1., 0., 0., 1., 0., 1.],
[0., 1., 1., 0., 0., 1.]])
Por defecto, los valores que puede tomar cada característica se infieren automáticamente del conjunto de datos y se pueden encontrar en el atributo categories_:
>>> enc.categories_
[array(['female', 'male'], dtype=object), array(['from Europe', 'from US'], dtype=object), array(['uses Firefox', 'uses Safari'], dtype=object)]
Es posible especificar esto explícitamente utilizando el parámetro ``categories`. En nuestro conjunto de datos hay dos géneros, cuatro continentes posibles y cuatro navegadores web:
>>> genders = ['female', 'male']
>>> locations = ['from Africa', 'from Asia', 'from Europe', 'from US']
>>> browsers = ['uses Chrome', 'uses Firefox', 'uses IE', 'uses Safari']
>>> enc = preprocessing.OneHotEncoder(categories=[genders, locations, browsers])
>>> # Note that for there are missing categorical values for the 2nd and 3rd
>>> # feature
>>> X = [['male', 'from US', 'uses Safari'], ['female', 'from Europe', 'uses Firefox']]
>>> enc.fit(X)
OneHotEncoder(categories=[['female', 'male'],
['from Africa', 'from Asia', 'from Europe',
'from US'],
['uses Chrome', 'uses Firefox', 'uses IE',
'uses Safari']])
>>> enc.transform([['female', 'from Asia', 'uses Chrome']]).toarray()
array([[1., 0., 0., 1., 0., 0., 1., 0., 0., 0.]])
Si existe la posibilidad de que los datos de entrenamiento puedan tener características categóricas perdidas, a menudo puede ser mejor especificar handle_unknown='ignore' en lugar de establecer las categories manualmente como arriba. Cuando se especifica handle_unknown='ignore' y se encuentran categorías desconocidas durante la transformación, no se producirá ningún error, pero las columnas codificadas en one-hot para esta característica serán todos ceros (``handle_unknown=”ignore”` sólo se admite para la codificación one-hot):
>>> enc = preprocessing.OneHotEncoder(handle_unknown='ignore')
>>> X = [['male', 'from US', 'uses Safari'], ['female', 'from Europe', 'uses Firefox']]
>>> enc.fit(X)
OneHotEncoder(handle_unknown='ignore')
>>> enc.transform([['female', 'from Asia', 'uses Chrome']]).toarray()
array([[1., 0., 0., 0., 0., 0.]])
También es posible codificar cada columna en n_categories - 1 columnas en lugar de n_categories columnas usando el parámetro drop. Este parámetro permite al usuario especificar una categoría para cada característica que se va a descartar. Esto es útil para evitar la colinealidad en la matriz de entrada en algunos clasificadores. Esta funcionalidad es útil, por ejemplo, cuando se utiliza una regresión no regularizada (LinearRegression), ya que la colinealidad haría que la matriz de covarianzas no fuera invertible. Cuando este parámetro no None, handle_unknown debe establecerse como error:
>>> X = [['male', 'from US', 'uses Safari'],
... ['female', 'from Europe', 'uses Firefox']]
>>> drop_enc = preprocessing.OneHotEncoder(drop='first').fit(X)
>>> drop_enc.categories_
[array(['female', 'male'], dtype=object), array(['from Europe', 'from US'], dtype=object), array(['uses Firefox', 'uses Safari'], dtype=object)]
>>> drop_enc.transform(X).toarray()
array([[1., 1., 1.],
[0., 0., 0.]])
Es posible que quieras eliminar una de las dos columnas sólo para las características con 2 categorías. En este caso, puedes establecer el parámetro drop='if_binary'.
>>> X = [['male', 'US', 'Safari'],
... ['female', 'Europe', 'Firefox'],
... ['female', 'Asia', 'Chrome']]
>>> drop_enc = preprocessing.OneHotEncoder(drop='if_binary').fit(X)
>>> drop_enc.categories_
[array(['female', 'male'], dtype=object), array(['Asia', 'Europe', 'US'], dtype=object), array(['Chrome', 'Firefox', 'Safari'], dtype=object)]
>>> drop_enc.transform(X).toarray()
array([[1., 0., 0., 1., 0., 0., 1.],
[0., 0., 1., 0., 0., 1., 0.],
[0., 1., 0., 0., 1., 0., 0.]])
En la transformada X, la primera columna es la codificación de la característica con las categorías «male»/»female», mientras que las 6 columnas restantes son la codificación de las 2 características con respectivamente 3 categorías cada una.
OneHotEncoder soporta características categóricas con valores faltantes considerando los valores faltantes como una categoría adicional:
>>> X = [['male', 'Safari'],
... ['female', None],
... [np.nan, 'Firefox']]
>>> enc = preprocessing.OneHotEncoder(handle_unknown='error').fit(X)
>>> enc.categories_
[array(['female', 'male', nan], dtype=object),
array(['Firefox', 'Safari', None], dtype=object)]
>>> enc.transform(X).toarray()
array([[0., 1., 0., 0., 1., 0.],
[1., 0., 0., 0., 0., 1.],
[0., 0., 1., 1., 0., 0.]])
Si una característica contiene tanto np.nan como None se considerarán categorías separadas:
>>> X = [['Safari'], [None], [np.nan], ['Firefox']]
>>> enc = preprocessing.OneHotEncoder(handle_unknown='error').fit(X)
>>> enc.categories_
[array(['Firefox', 'Safari', None, nan], dtype=object)]
>>> enc.transform(X).toarray()
array([[0., 1., 0., 0.],
[0., 0., 1., 0.],
[0., 0., 0., 1.],
[1., 0., 0., 0.]])
Ver Cargando características desde diccionarios para características categóricas que se representan como un diccionario (dict), no como escalares.
6.3.5. Discretización¶
Discretización (también conocida como cuantificación o binning) proporciona una forma de dividir características continuas en valores discretos. Ciertos conjuntos de datos con características continuas pueden beneficiarse de la discretización, ya que ésta puede transformar el conjunto de datos de atributos continuos en uno con sólo atributos nominales.
Las características discretizadas codificadas en One-hot pueden hacer que un modelo sea más expresivo, manteniendo al mismo tiempo la capacidad de interpretación. Por ejemplo, el preprocesamiento con un discretizador puede introducir la no linealidad en los modelos lineales.
6.3.5.1. Discretización K-clases o intervalos de clase¶
KBinsDiscretizer discretiza las características en k intervalos de clases:
>>> X = np.array([[ -3., 5., 15 ],
... [ 0., 6., 14 ],
... [ 6., 3., 11 ]])
>>> est = preprocessing.KBinsDiscretizer(n_bins=[3, 2, 2], encode='ordinal').fit(X)
Por defecto, la salida está codificada one-hot en una matriz dispersa (Ver Codificación de características categóricas) y esto puede configurarse con el parámetro encode. Para cada característica, los límites del intervalo de clase se calculan durante el fit y junto con el número de intervalos de clase, definirán los intervalos. Por lo tanto, para el ejemplo actual, estos intervalos se definen como:
característica 1: \({[-\infty, -1), [-1, 2), [2, \infty)}\)
característica 2: \({[-\infty, 5), [5, \infty)}\)
característica 3: \({[-\infty, 14), [14, \infty)}\)
Basado en estos intervalos de clase, X se transforma de la siguiente manera:
>>> est.transform(X)
array([[ 0., 1., 1.],
[ 1., 1., 1.],
[ 2., 0., 0.]])
El conjunto de datos resultante contiene atributos ordinales que pueden utilizarse posteriormente en un Pipeline.
La discretización es similar a la construcción de histogramas para datos continuos. Sin embargo, los histogramas se centran en el recuento de características que caen en determinados intervalos de clase, mientras que la discretización se centra en asignar valores de características a estos intervalos de clases.
KBinsDiscretizer implementa diferentes estrategias de binning, que se pueden seleccionar con el parámetro strategy. La estrategia ``uniform”” utiliza intervalos de clase de ancho constante. La estrategia “quantile” utiliza los valores cuantiles para tener intervalos de claase igualmente poblados en cada característica. La estrategia «kmeans» define los intervalos basándose en un procedimiento de agrupamiento por k-medias realizado en cada característica de forma independiente.
Ten en cuenta que puedes especificar intervalos de clase personalizados pasando un invocable que defina la estrategia de discretización a FunctionTransformer. Por ejemplo, podemos utilizar la función de Pandas pandas.cut:
>>> import pandas as pd
>>> import numpy as np
>>> bins = [0, 1, 13, 20, 60, np.inf]
>>> labels = ['infant', 'kid', 'teen', 'adult', 'senior citizen']
>>> transformer = preprocessing.FunctionTransformer(
... pd.cut, kw_args={'bins': bins, 'labels': labels, 'retbins': False}
... )
>>> X = np.array([0.2, 2, 15, 25, 97])
>>> transformer.fit_transform(X)
['infant', 'kid', 'teen', 'adult', 'senior citizen']
Categories (5, object): ['infant' < 'kid' < 'teen' < 'adult' < 'senior citizen']
6.3.5.2. Binarización de característica¶
La binarización de características es el proceso de fijar umbrales de las características numéricas para obtener valores booleanos. Esto puede ser útil para estimadores probabilísticos posteriores que suponen que los datos de entrada se distribuyen según una distribución Bernoulli multivariante. Por ejemplo, este es el caso de BernoulliRBM.
También es común entre la comunidad de procesadores de texto utilizar valores binarios de las características (probablemente para simplificar el razonamiento probabilístico) aunque los recuentos normalizados (también conocidos como frecuencias de términos) o las características con valores TF-IDF suelen tener un rendimiento ligeramente superior en la práctica.
En cuanto al Normalizer, la clase de utilidad Binarizer está pensada para ser utilizada en las primeras etapas de Pipeline. El método fit no hace nada ya que cada muestra es tratada independientemente de las demás:
>>> X = [[ 1., -1., 2.],
... [ 2., 0., 0.],
... [ 0., 1., -1.]]
>>> binarizer = preprocessing.Binarizer().fit(X) # fit does nothing
>>> binarizer
Binarizer()
>>> binarizer.transform(X)
array([[1., 0., 1.],
[1., 0., 0.],
[0., 1., 0.]])
Es posible ajustar el umbral del binarizador:
>>> binarizer = preprocessing.Binarizer(threshold=1.1)
>>> binarizer.transform(X)
array([[0., 0., 1.],
[1., 0., 0.],
[0., 0., 0.]])
En cuanto a la clase Normalizer, el módulo de preprocesamiento proporciona una función complementaria binarize para ser utilizada cuando la API del transformador no es necesaria.
Ten en cuenta que el Binarizer es similar al KBinsDiscretizer cuando k = 2, y cuando el límite del intervalo de clase está en el valor threshold.
Entrada dispersa
binarize y Binarizer aceptan tanto array-like densos como matrices dispersas de scipy.sparse como entrada.
Para la entrada dispersa los datos son **convertidos a la representación Filas Dispersas Comprimidas ** (ver scipy.sparse.csr_matrix). Para evitar copias de memoria innecesarias, se recomienda elegir la representación CSR antes.
6.3.6. Imputación de valores faltantes¶
Las herramientas para la imputación de valores faltantes se discuten en Imputación de valores faltantes.
6.3.7. Generación de características polinomiales¶
A menudo es útil añadir complejidad al modelo considerando características no lineales de los datos de entrada. Un método simple y común para utilizar son las características polinomiales, que permiten obtener los términos de alto orden e interacción de las características. Se implementa en PolinnomialFeatures:
>>> import numpy as np
>>> from sklearn.preprocessing import PolynomialFeatures
>>> X = np.arange(6).reshape(3, 2)
>>> X
array([[0, 1],
[2, 3],
[4, 5]])
>>> poly = PolynomialFeatures(2)
>>> poly.fit_transform(X)
array([[ 1., 0., 1., 0., 0., 1.],
[ 1., 2., 3., 4., 6., 9.],
[ 1., 4., 5., 16., 20., 25.]])
Las características de X han sido transformadas de \((X_1, X_2)\) a \((1, X_1, X_2, X_1^2, X_1X_2, X_2^2)\).
En algunos casos, sólo se requieren términos de interacción entre las características, y se pueden conseguir con el ajuste interaction_only=True:
>>> X = np.arange(9).reshape(3, 3)
>>> X
array([[0, 1, 2],
[3, 4, 5],
[6, 7, 8]])
>>> poly = PolynomialFeatures(degree=3, interaction_only=True)
>>> poly.fit_transform(X)
array([[ 1., 0., 1., 2., 0., 0., 2., 0.],
[ 1., 3., 4., 5., 12., 15., 20., 60.],
[ 1., 6., 7., 8., 42., 48., 56., 336.]])
Las características de X han sido transformadas de \((X_1, X_2, X_3)\) a \((1, X_1, X_2, X_3, X_1X_2, X_1X_3, X_2X_3, X_1X_2X_3)\).
Ten en cuenta que las características polinómicas se utilizan implícitamente en los métodos del kernel (por ejemplo, SVC, KernelPCA) cuando se utilizan polinomios Funciones del núcleo.
Ver Interpolación polinómica para la Regresión de Cresta usando características polinomiales creadas.
6.3.8. Transformadores personalizados¶
A menudo, querrás convertir una función existente de Python en un transformador para ayudar a limpiar o procesar datos. Puedes implementar un transformador desde una función arbitraria con FunctionTransformer. Por ejemplo, para construir un transformador que aplique una transformación de registro en un pipeline, haz:
>>> import numpy as np
>>> from sklearn.preprocessing import FunctionTransformer
>>> transformer = FunctionTransformer(np.log1p, validate=True)
>>> X = np.array([[0, 1], [2, 3]])
>>> transformer.transform(X)
array([[0. , 0.69314718],
[1.09861229, 1.38629436]])
Puedes asegurarte de que func e inverse_func son la inversa de los demás configurando check_inverse=True y llamando fit antes de transform. Por favor, ten en cuenta que se producirá una advertencia y se puede convertir en un error con un filterwarnings:
>>> import warnings
>>> warnings.filterwarnings("error", message=".*check_inverse*.",
... category=UserWarning, append=False)
Para ver un ejemplo de código completo que demuestra el uso de FunctionTransformer para extraer características de los datos de texto consulta Transformador de columnas con fuentes de datos heterogéneas
