Compara el efecto de los diferentes escaladores en los datos con los atípicos

La característica 0 (mediana de ingresos en un bloque) y la característica 5 (número de hogares) del conjunto de datos Conjunto de datos California Housing tienen escalas muy diferentes y contienen algunos valores atípicos muy grandes. Estas dos características dificultan la visualización de los datos y, lo que es más importante, pueden degradar el rendimiento predictivo de muchos algoritmos de aprendizaje automático. Los datos no escalados también pueden ralentizar o incluso impedir la convergencia de muchos estimadores basados en el gradiente.

De hecho, muchos estimadores están diseñados con la suposición de que cada característica tiene valores cercanos a cero o más importante que todas las características varían en escalas comparables. En particular, los estimadores basados en métricas y basados en degradados suelen asumir aproximadamente datos estandarizados (características centradas con varianzas unitarias). Una excepción notable son los estimadores basados en árboles de decisiones que son robustos a la escala arbitraria de los datos.

Este ejemplo utiliza diferentes escaladores, transformadores y normalizadores para llevar los datos dentro de un rango predefinido.

Los escaladores son transformadores lineales (o más precisamente) y difieren unos de otros en la forma en que estiman los parámetros utilizados para cambiar y escalar cada característica.

QuantileTransformer proporciona transformaciones no lineales en las que se reducen las distancias entre los valores marginales atípicos y los valores atípicos. PowerTransformer proporciona transformaciones no lineales en las que los datos se asignan a una distribución normal para estabilizar la varianza y minimizar la asimetría.

A diferencia de las transformaciones anteriores, la normalización se refiere a una transformación por muestra en lugar de una transformación por característica.

El siguiente código es un poco verboso, siéntete libre de saltar directamente al análisis de los resultados.

# Author:  Raghav RV <rvraghav93@gmail.com>
#          Guillaume Lemaitre <g.lemaitre58@gmail.com>
#          Thomas Unterthiner
# License: BSD 3 clause

import numpy as np

import matplotlib as mpl
from matplotlib import pyplot as plt
from matplotlib import cm

from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import minmax_scale
from sklearn.preprocessing import MaxAbsScaler
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import RobustScaler
from sklearn.preprocessing import Normalizer
from sklearn.preprocessing import QuantileTransformer
from sklearn.preprocessing import PowerTransformer

from sklearn.datasets import fetch_california_housing

print(__doc__)

dataset = fetch_california_housing()
X_full, y_full = dataset.data, dataset.target

# Take only 2 features to make visualization easier
# Feature of 0 has a long tail distribution.
# Feature 5 has a few but very large outliers.

X = X_full[:, [0, 5]]

distributions = [
    ('Unscaled data', X),
    ('Data after standard scaling',
        StandardScaler().fit_transform(X)),
    ('Data after min-max scaling',
        MinMaxScaler().fit_transform(X)),
    ('Data after max-abs scaling',
        MaxAbsScaler().fit_transform(X)),
    ('Data after robust scaling',
        RobustScaler(quantile_range=(25, 75)).fit_transform(X)),
    ('Data after power transformation (Yeo-Johnson)',
     PowerTransformer(method='yeo-johnson').fit_transform(X)),
    ('Data after power transformation (Box-Cox)',
     PowerTransformer(method='box-cox').fit_transform(X)),
    ('Data after quantile transformation (uniform pdf)',
        QuantileTransformer(output_distribution='uniform')
        .fit_transform(X)),
    ('Data after quantile transformation (gaussian pdf)',
        QuantileTransformer(output_distribution='normal')
        .fit_transform(X)),
    ('Data after sample-wise L2 normalizing',
        Normalizer().fit_transform(X)),
]

# scale the output between 0 and 1 for the colorbar
y = minmax_scale(y_full)

# plasma does not exist in matplotlib < 1.5
cmap = getattr(cm, 'plasma_r', cm.hot_r)

def create_axes(title, figsize=(16, 6)):
    fig = plt.figure(figsize=figsize)
    fig.suptitle(title)

    # define the axis for the first plot
    left, width = 0.1, 0.22
    bottom, height = 0.1, 0.7
    bottom_h = height + 0.15
    left_h = left + width + 0.02

    rect_scatter = [left, bottom, width, height]
    rect_histx = [left, bottom_h, width, 0.1]
    rect_histy = [left_h, bottom, 0.05, height]

    ax_scatter = plt.axes(rect_scatter)
    ax_histx = plt.axes(rect_histx)
    ax_histy = plt.axes(rect_histy)

    # define the axis for the zoomed-in plot
    left = width + left + 0.2
    left_h = left + width + 0.02

    rect_scatter = [left, bottom, width, height]
    rect_histx = [left, bottom_h, width, 0.1]
    rect_histy = [left_h, bottom, 0.05, height]

    ax_scatter_zoom = plt.axes(rect_scatter)
    ax_histx_zoom = plt.axes(rect_histx)
    ax_histy_zoom = plt.axes(rect_histy)

    # define the axis for the colorbar
    left, width = width + left + 0.13, 0.01

    rect_colorbar = [left, bottom, width, height]
    ax_colorbar = plt.axes(rect_colorbar)

    return ((ax_scatter, ax_histy, ax_histx),
            (ax_scatter_zoom, ax_histy_zoom, ax_histx_zoom),
            ax_colorbar)


def plot_distribution(axes, X, y, hist_nbins=50, title="",
                      x0_label="", x1_label=""):
    ax, hist_X1, hist_X0 = axes

    ax.set_title(title)
    ax.set_xlabel(x0_label)
    ax.set_ylabel(x1_label)

    # The scatter plot
    colors = cmap(y)
    ax.scatter(X[:, 0], X[:, 1], alpha=0.5, marker='o', s=5, lw=0, c=colors)

    # Removing the top and the right spine for aesthetics
    # make nice axis layout
    ax.spines['top'].set_visible(False)
    ax.spines['right'].set_visible(False)
    ax.get_xaxis().tick_bottom()
    ax.get_yaxis().tick_left()
    ax.spines['left'].set_position(('outward', 10))
    ax.spines['bottom'].set_position(('outward', 10))

    # Histogram for axis X1 (feature 5)
    hist_X1.set_ylim(ax.get_ylim())
    hist_X1.hist(X[:, 1], bins=hist_nbins, orientation='horizontal',
                 color='grey', ec='grey')
    hist_X1.axis('off')

    # Histogram for axis X0 (feature 0)
    hist_X0.set_xlim(ax.get_xlim())
    hist_X0.hist(X[:, 0], bins=hist_nbins, orientation='vertical',
                 color='grey', ec='grey')
    hist_X0.axis('off')

Se mostrarán dos gráficos para cada escalador/normalizador/transformador. La figura de la izquierda mostrará un gráfico de dispersión del conjunto de datos completo, mientras que la figura de la derecha excluirá los valores extremos considerando sólo el 99% del conjunto de datos, excluyendo los valores atípicos marginales. Además, las distribuciones marginales de cada característica se mostrarán a los lados del gráfico de dispersión.

def make_plot(item_idx):
    title, X = distributions[item_idx]
    ax_zoom_out, ax_zoom_in, ax_colorbar = create_axes(title)
    axarr = (ax_zoom_out, ax_zoom_in)
    plot_distribution(axarr[0], X, y, hist_nbins=200,
                      x0_label="Median Income",
                      x1_label="Number of households",
                      title="Full data")

    # zoom-in
    zoom_in_percentile_range = (0, 99)
    cutoffs_X0 = np.percentile(X[:, 0], zoom_in_percentile_range)
    cutoffs_X1 = np.percentile(X[:, 1], zoom_in_percentile_range)

    non_outliers_mask = (
        np.all(X > [cutoffs_X0[0], cutoffs_X1[0]], axis=1) &
        np.all(X < [cutoffs_X0[1], cutoffs_X1[1]], axis=1))
    plot_distribution(axarr[1], X[non_outliers_mask], y[non_outliers_mask],
                      hist_nbins=50,
                      x0_label="Median Income",
                      x1_label="Number of households",
                      title="Zoom-in")

    norm = mpl.colors.Normalize(y_full.min(), y_full.max())
    mpl.colorbar.ColorbarBase(ax_colorbar, cmap=cmap,
                              norm=norm, orientation='vertical',
                              label='Color mapping for values of y')

Datos originales

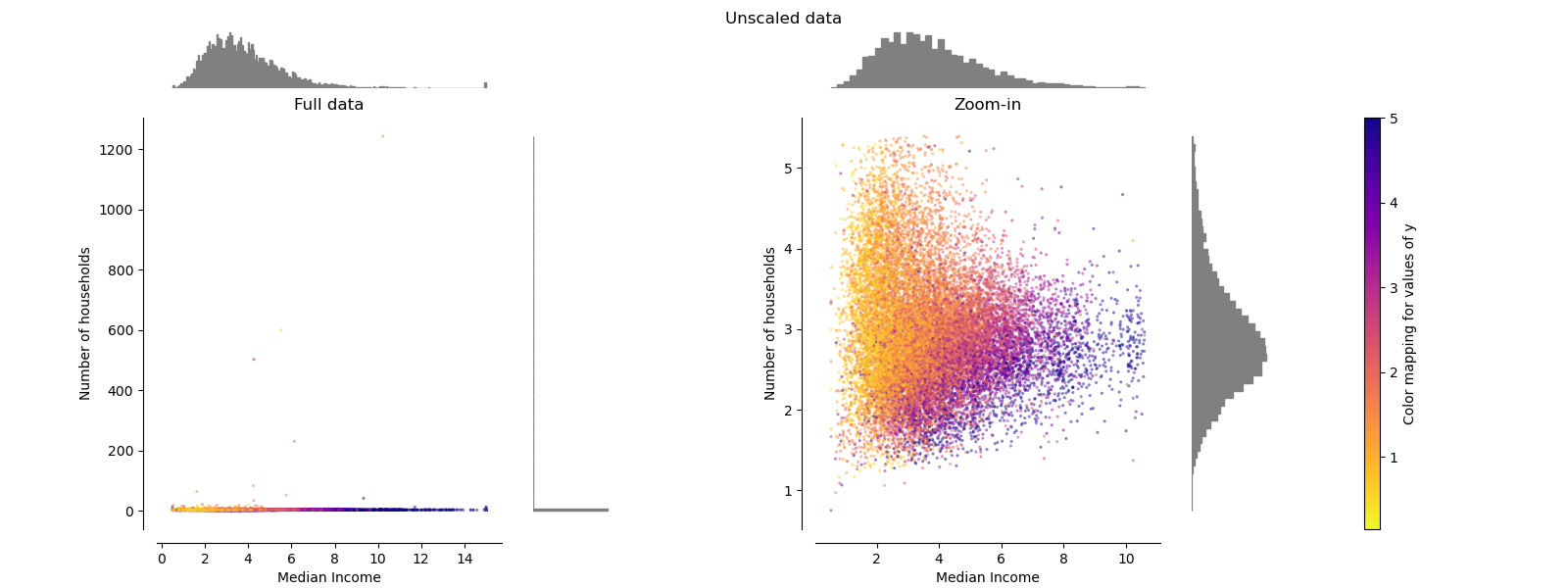
Cada transformación se traza mostrando dos características transformadas, con el gráfico de la izquierda mostrando el conjunto de datos, y el de la derecha ampliado para mostrar el conjunto de datos sin los valores marginales. La gran mayoría de las muestras están compactadas en un rango específico, [0, 10] para la mediana de ingresos y [0, 6] para el número de hogares. Observa que hay algunos valores atípicos marginales (algunos bloques tienen más de 1.200 hogares). Por lo tanto, un preprocesamiento específico puede ser muy beneficioso dependiendo de la aplicación. A continuación, presentamos algunas ideas y comportamientos de esos métodos de preprocesamiento en presencia de valores atípicos marginales.

make_plot(0)

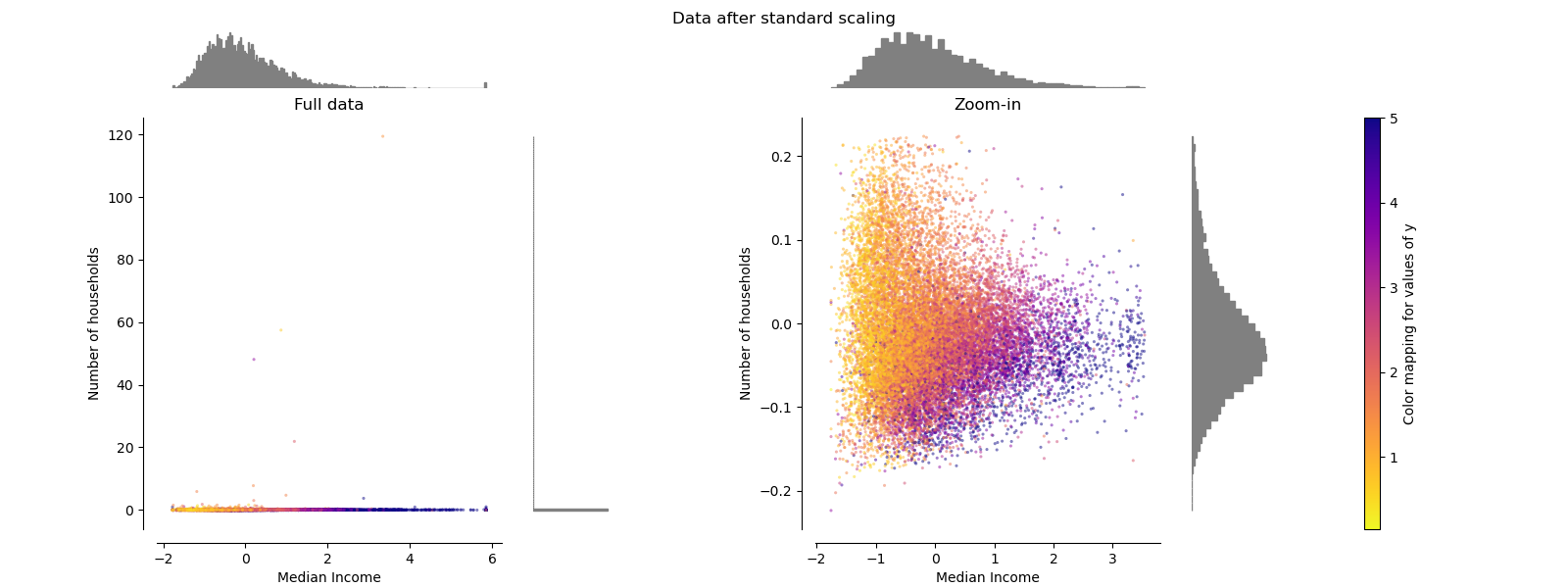
StandardScaler

StandardScaler elimina la media y escala los datos a la unidad de varianza. El escalado reduce el rango de los valores de las características como se muestra en la figura de la izquierda. Sin embargo, los valores atípicos influyen en el cálculo de la media empírica y la desviación estándar. Observa, en particular, que debido a que los valores atípicos de cada característica tienen diferentes magnitudes, la dispersión de los datos transformados de cada característica es muy diferente: la mayoría de los datos se encuentran en el intervalo [-2, 4] para la característica transformada de la mediana de los ingresos, mientras que los mismos datos están comprimidos en el intervalo más pequeño [-0,2, 0,2] para la transformación del número de hogares.

StandardScaler por lo tanto no puede garantizar escalas de características equilibradas en presencia de valores atípicos.

make_plot(1)

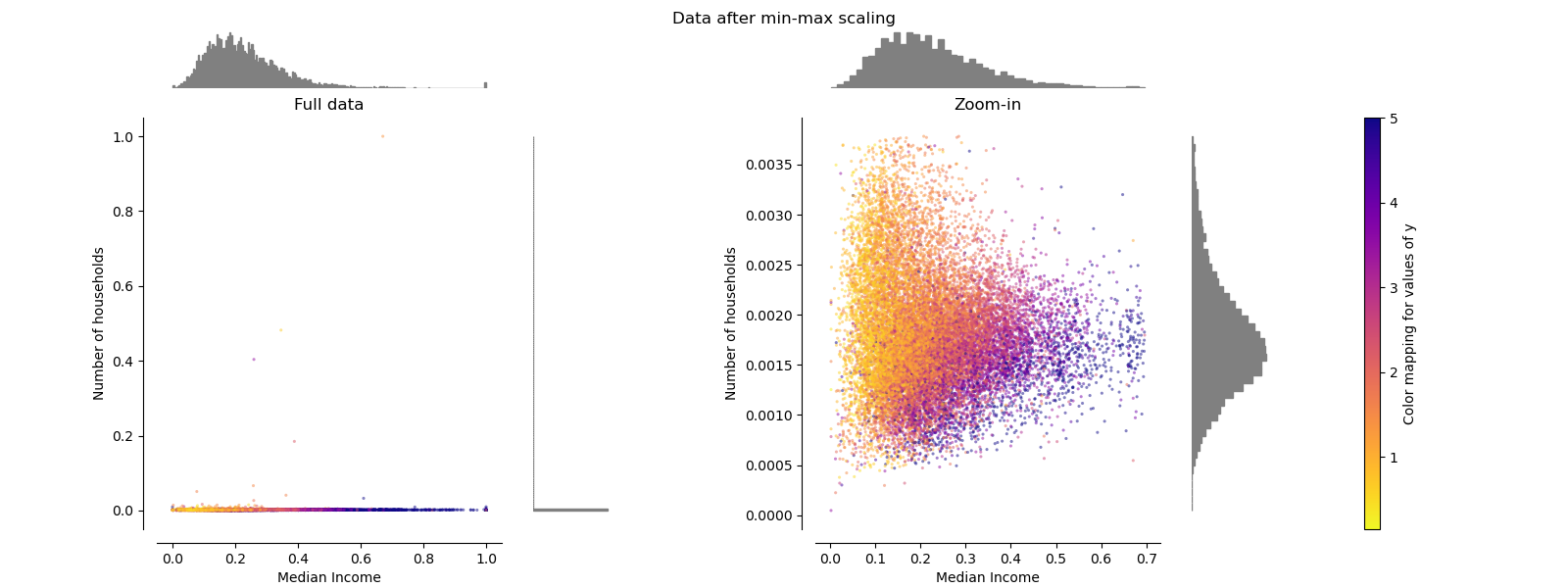
MinMaxScaler

MinMaxScaler reescala el conjunto de datos de forma que todos los valores de las características estén en el rango [0, 1], como se muestra en el panel derecho de abajo. Sin embargo, este escalado comprime todos los valores típicos en el estrecho rango [0, 0,005] para el número transformado de hogares.

Tanto StandardScaler como MinMaxScaler son muy sensibles a la presencia de valores atípicos.

make_plot(2)

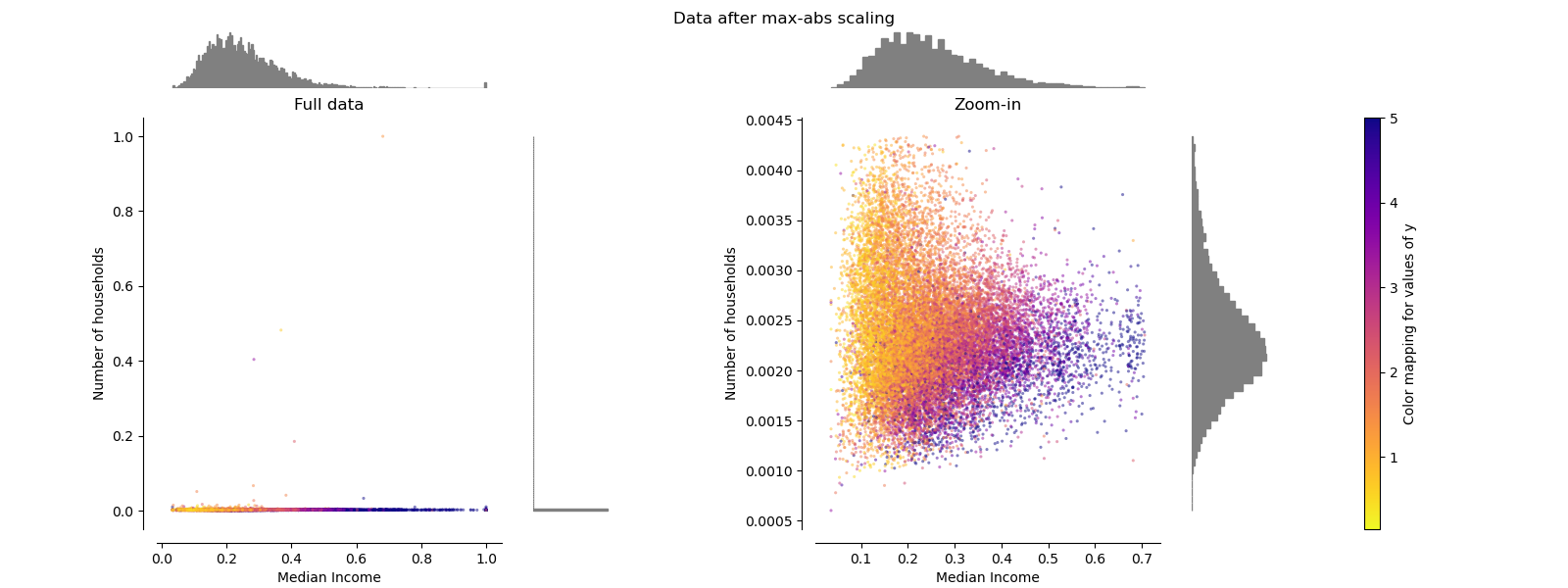
MaxAbsScaler

MaxAbsScaler es similar a MinMaxScaler excepto que los valores se mapean en el rango [0, 1]. En datos sólo positivos, ambos escaladores se comportan de manera similar. MaxAbsScaler por lo tanto también sufre la presencia de grandes valores atípicos.

make_plot(3)

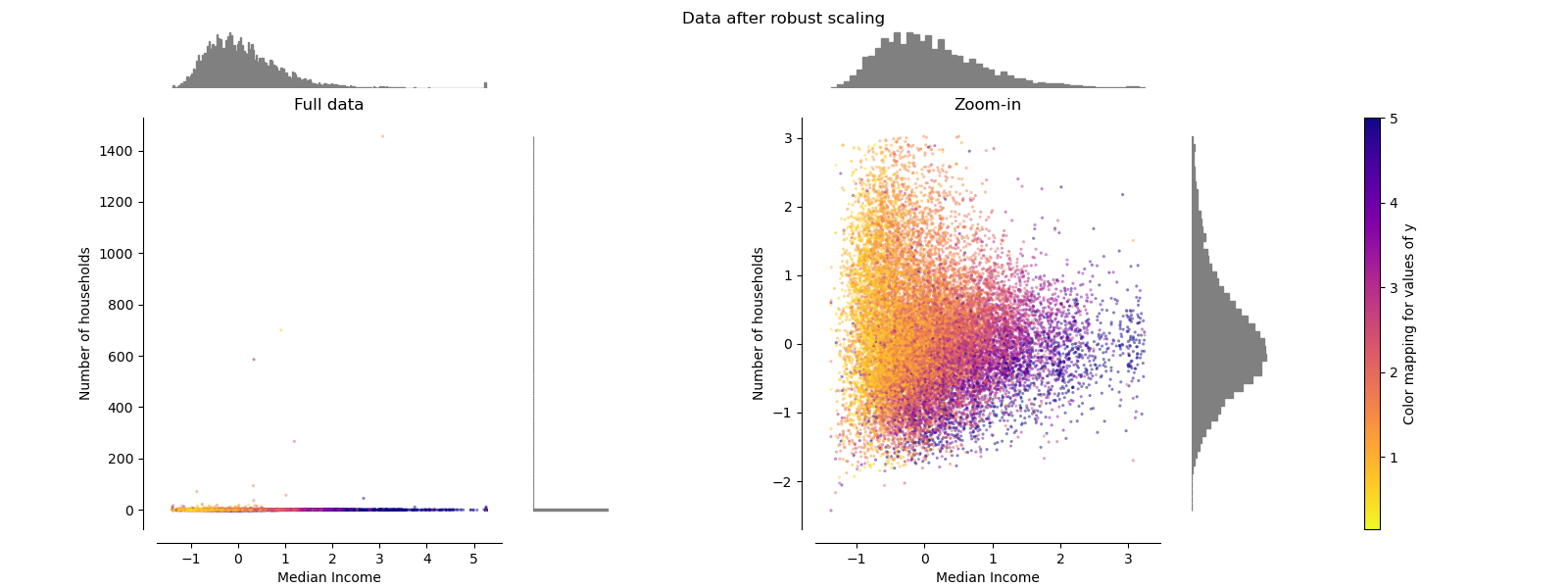
RobustScaler

A diferencia de los escaladores anteriores, las estadísticas de centrado y escalado de RobustScaler se basan en percentiles y, por lo tanto, no están influidas por un número reducido de valores atípicos marginales muy grandes. En consecuencia, el rango resultante de los valores de las características transformadas es mayor que el de los escaladores anteriores y, lo que es más importante, son aproximadamente similares: para ambas características la mayoría de los valores transformados se encuentran en un rango de [-2, 3], como se ve en la figura ampliada. Observa que los propios valores atípicos siguen estando presentes en los datos transformados. Si se desea un recorte independiente de los valores atípicos, se requiere una transformación no lineal (ver más adelante).

make_plot(4)

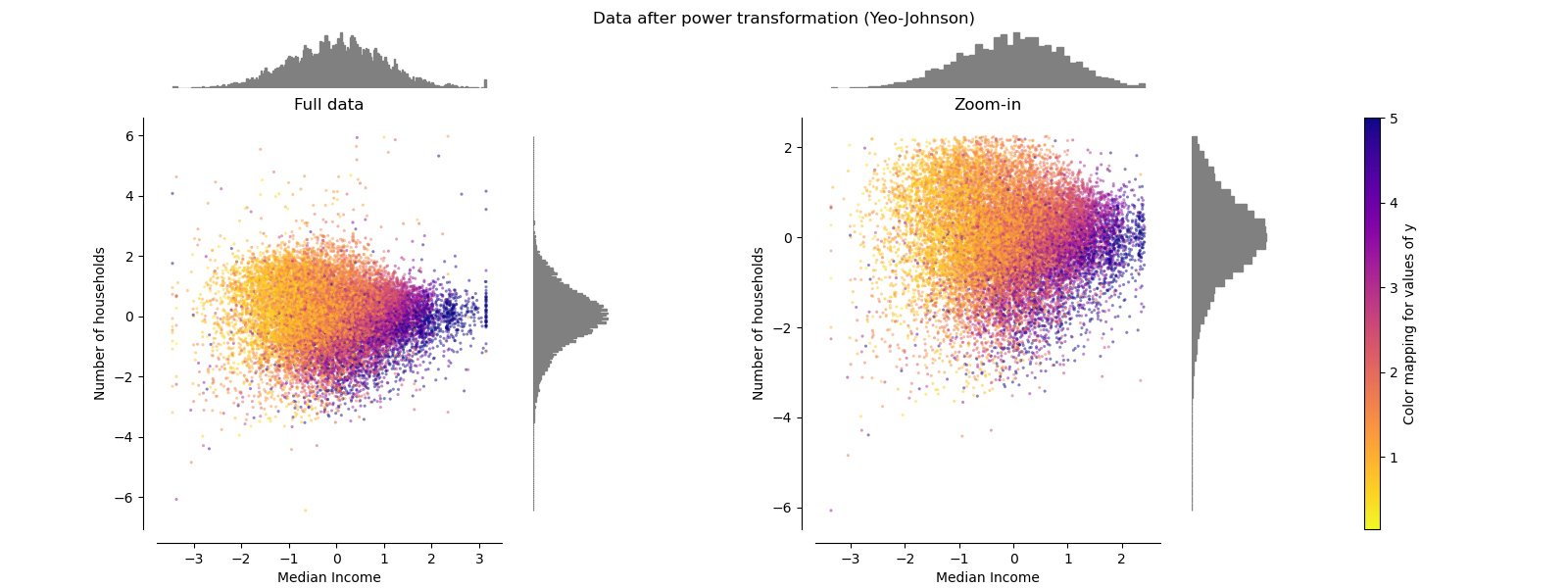
PowerTransformer

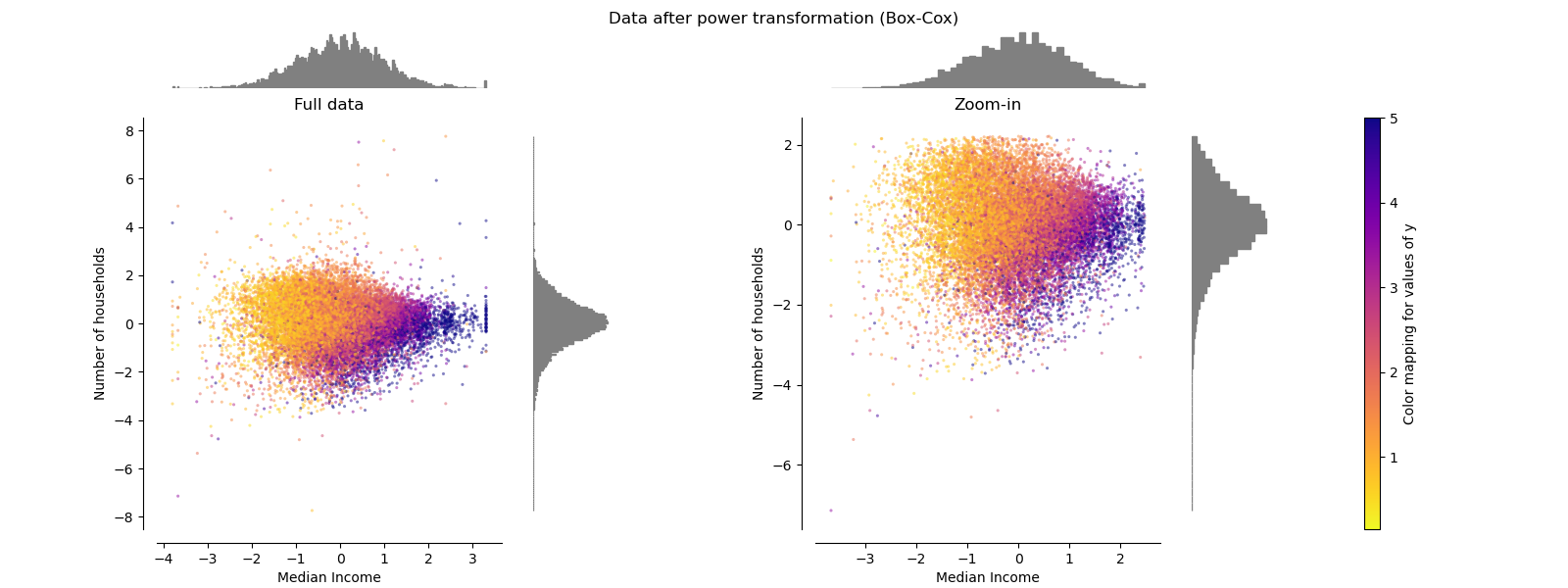
PowerTransformer aplica una transformación de potencia a cada característica para hacer los datos más gaussianos con el fin de estabilizar la varianza y minimizar la asimetría. Actualmente se soportan las transformaciones Yeo-Johnson y Box-Cox, y el factor de escala óptimo se determina mediante una estimación de máxima verosimilitud en ambos métodos. Por defecto, PowerTransformer aplica una normalización de media cero y varianza unitaria. Ten en cuenta que Box-Cox sólo puede aplicarse a datos estrictamente positivos. Los ingresos y el número de hogares son estrictamente positivos, pero si hay valores negativos se prefiere la transformación de Yeo-Johnson.

make_plot(5)
make_plot(6)

• 
• 

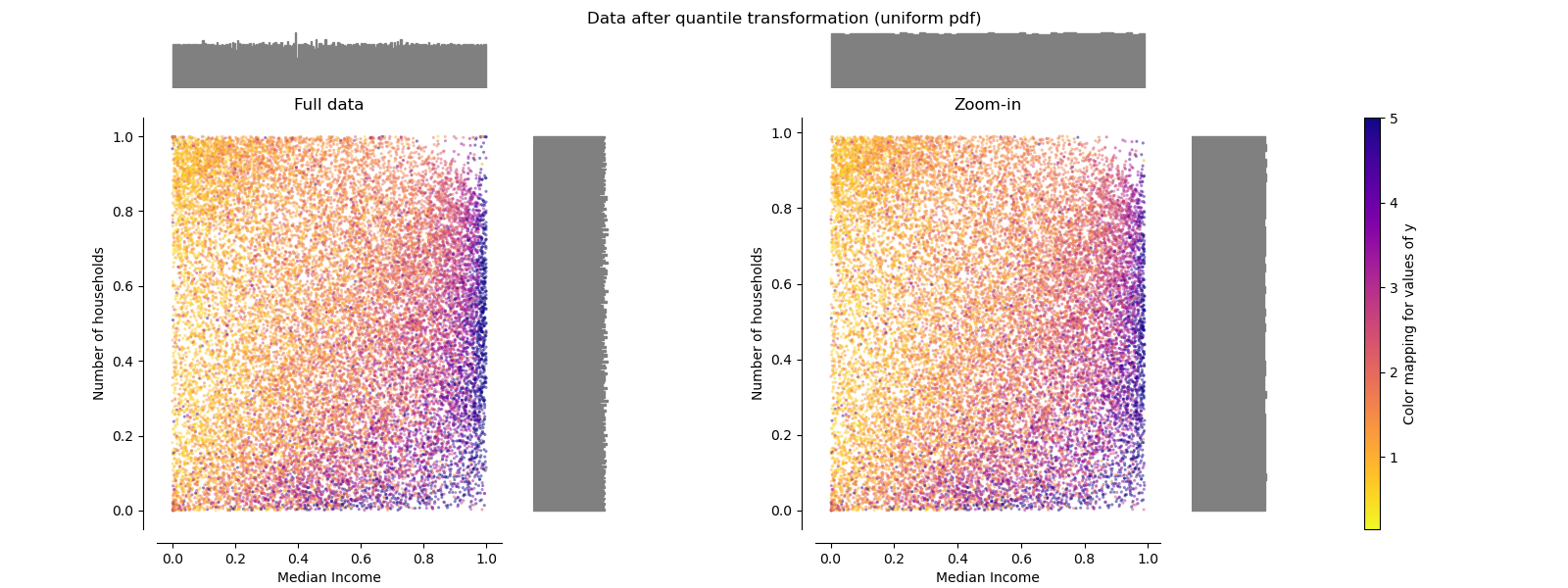
QuantileTransformer (salida uniforme)

QuantileTransformer aplica una transformación no lineal de tal manera que la función de densidad de probabilidad de cada característica será mapeada a una distribución uniforme o gaussiana. En este caso, todos los datos, incluidos los valores atípicos, se asignarán a una distribución uniforme con el rango [0, 1], haciendo que los valores atípicos sean indistinguibles de los valores típicos.

RobustScaler y QuantileTransformer son robustos a los valores atípicos en el sentido de que añadir o eliminar valores atípicos en el conjunto de entrenamiento producirá aproximadamente la misma transformación. Pero al contrario que RobustScaler, QuantileTransformer también colapsará automáticamente cualquier valor atípico ajustándolo a los límites de rango definidos a priori (0 y 1). Esto puede dar lugar a artefactos de saturación para los valores extremos.

make_plot(7)

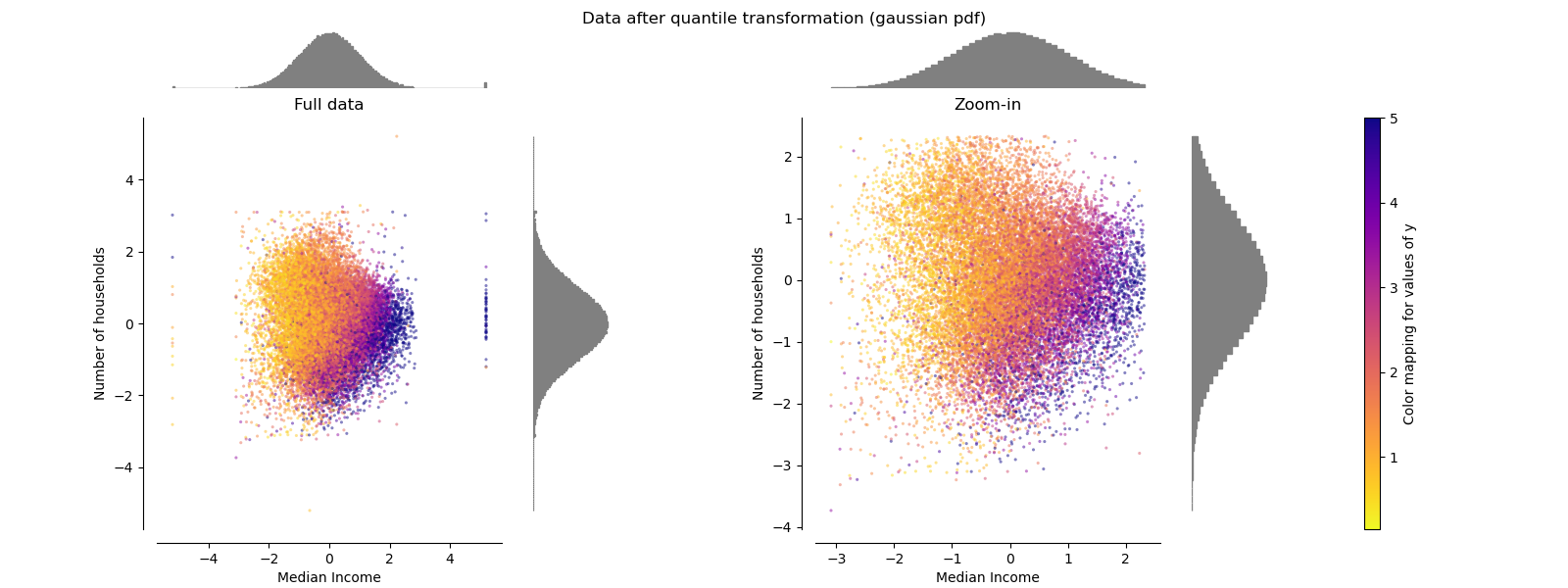
QuantileTransformer (salida gaussiana)

Para mapear a una distribución Gaussian, establezca el parámetro output_distribution='normal'.

make_plot(8)

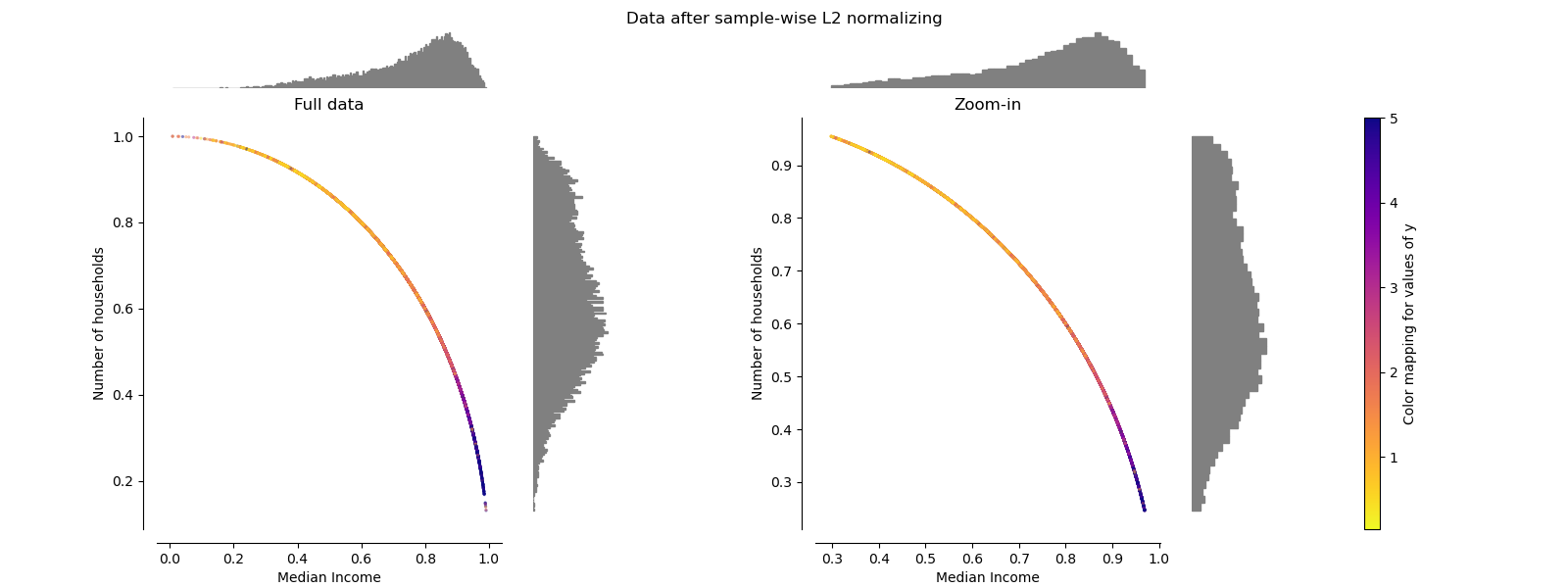
Normalizador

El Normalizer reescala el vector de cada muestra para que tenga norma unitaria, independientemente de la distribución de las muestras. Se puede ver en las dos figuras de abajo donde todas las muestras son mapeadas en el círculo de la unidad. En nuestro ejemplo, las dos características seleccionadas sólo tienen valores positivos, por lo que los datos transformados sólo se encuentran en el cuadrante positivo. Este no sería el caso si algunas características originales tuvieran una mezcla de valores positivos y negativos.

make_plot(9)

plt.show()