Usar KBinsDiscretizer para discretizar características continuas

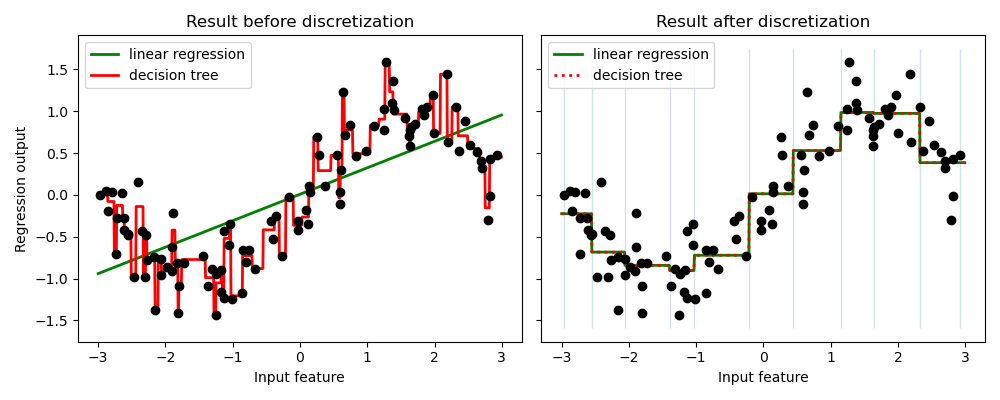
El ejemplo compara el resultado de la predicción de regresión lineal (modelo lineal) y el árbol de decisiones (modelo basado en árboles) con y sin discretización de las características valoradas en realidad.

Como se muestra en el resultado antes de la discretización, el modelo lineal es rápido de construir y relativamente sencillo de interpretar, pero sólo puede modelar relaciones lineales, mientras que el árbol de decisión puede construir un modelo mucho más complejo de los datos. Una forma de hacer que el modelo lineal sea más potente en datos continuos es utilizar la discretización (también conocida como binning). En el ejemplo, discretizamos la característica y codificamos los datos transformados con un solo binario. Ten en cuenta que si los intervalos no son razonablemente amplios, parece que hay un riesgo sustancialmente mayor de sobreajuste, por lo que los parámetros del discretizador deben ajustarse normalmente bajo validación cruzada.

Tras la discretización, la regresión lineal y el árbol de decisión hacen exactamente la misma predicción. Como las características son constantes dentro de cada casilla, cualquier modelo debe predecir el mismo valor para todos los puntos de una casilla. En comparación con el resultado anterior a la discretización, el modelo lineal es mucho más flexible, mientras que el árbol de decisión es mucho menos flexible. Observa que la separación de las características no suele tener ningún efecto beneficioso para los modelos basados en árboles, ya que estos modelos pueden aprender a dividir los datos en cualquier lugar.

# Author: Andreas Müller
#         Hanmin Qin <qinhanmin2005@sina.com>
# License: BSD 3 clause

import numpy as np
import matplotlib.pyplot as plt

from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import KBinsDiscretizer
from sklearn.tree import DecisionTreeRegressor

print(__doc__)

# construct the dataset
rnd = np.random.RandomState(42)
X = rnd.uniform(-3, 3, size=100)
y = np.sin(X) + rnd.normal(size=len(X)) / 3
X = X.reshape(-1, 1)

# transform the dataset with KBinsDiscretizer
enc = KBinsDiscretizer(n_bins=10, encode='onehot')
X_binned = enc.fit_transform(X)

# predict with original dataset
fig, (ax1, ax2) = plt.subplots(ncols=2, sharey=True, figsize=(10, 4))
line = np.linspace(-3, 3, 1000, endpoint=False).reshape(-1, 1)
reg = LinearRegression().fit(X, y)
ax1.plot(line, reg.predict(line), linewidth=2, color='green',
         label="linear regression")
reg = DecisionTreeRegressor(min_samples_split=3, random_state=0).fit(X, y)
ax1.plot(line, reg.predict(line), linewidth=2, color='red',
         label="decision tree")
ax1.plot(X[:, 0], y, 'o', c='k')
ax1.legend(loc="best")
ax1.set_ylabel("Regression output")
ax1.set_xlabel("Input feature")
ax1.set_title("Result before discretization")

# predict with transformed dataset
line_binned = enc.transform(line)
reg = LinearRegression().fit(X_binned, y)
ax2.plot(line, reg.predict(line_binned), linewidth=2, color='green',
         linestyle='-', label='linear regression')
reg = DecisionTreeRegressor(min_samples_split=3,
                            random_state=0).fit(X_binned, y)
ax2.plot(line, reg.predict(line_binned), linewidth=2, color='red',
         linestyle=':', label='decision tree')
ax2.plot(X[:, 0], y, 'o', c='k')
ax2.vlines(enc.bin_edges_[0], *plt.gca().get_ylim(), linewidth=1, alpha=.2)
ax2.legend(loc="best")
ax2.set_xlabel("Input feature")
ax2.set_title("Result after discretization")

plt.tight_layout()
plt.show()