Efecto de la transformación de los objetivos en el modelo de regresión

En este ejemplo, damos una visión general de TransformedTargetRegressor. Utilizamos dos ejemplos para ilustrar las ventajas de transformar los objetivos antes de aprender un modelo de regresión lineal. El primer ejemplo utiliza datos sintéticos, mientras que el segundo se basa en el conjunto de datos de viviendas de Ames.

# Author: Guillaume Lemaitre <guillaume.lemaitre@inria.fr>
# License: BSD 3 clause

import numpy as np
import matplotlib
import matplotlib.pyplot as plt

from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.linear_model import RidgeCV
from sklearn.compose import TransformedTargetRegressor
from sklearn.metrics import median_absolute_error, r2_score
from sklearn.utils.fixes import parse_version

Ejemplo de síntesis

# `normed` is being deprecated in favor of `density` in histograms
if parse_version(matplotlib.__version__) >= parse_version('2.1'):
    density_param = {'density': True}
else:
    density_param = {'normed': True}

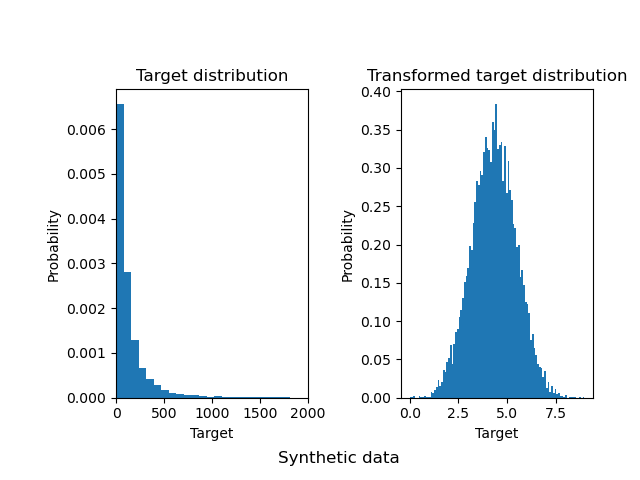
Se genera un conjunto de datos de regresión aleatoria sintética. Los objetivos y se modifican por:

1. traduciendo todos los objetivos de forma que todas las entradas sean no negativas (sumando el valor absoluto del menor y) y

2. aplicando una función exponencial para obtener objetivos no lineales que no pueden ajustarse mediante un modelo lineal simple.

Por lo tanto, se utilizará una función logarítmica (np.log1p) y una función exponencial (np.expm1) para transformar los objetivos antes de entrenar un modelo de regresión lineal y utilizarlo para la predicción.

X, y = make_regression(n_samples=10000, noise=100, random_state=0)
y = np.expm1((y + abs(y.min())) / 200)
y_trans = np.log1p(y)

A continuación, trazamos las funciones de densidad de probabilidad del objetivo antes y después de aplicar las funciones logarítmicas.

f, (ax0, ax1) = plt.subplots(1, 2)

ax0.hist(y, bins=100, **density_param)
ax0.set_xlim([0, 2000])
ax0.set_ylabel('Probability')
ax0.set_xlabel('Target')
ax0.set_title('Target distribution')

ax1.hist(y_trans, bins=100, **density_param)
ax1.set_ylabel('Probability')
ax1.set_xlabel('Target')
ax1.set_title('Transformed target distribution')

f.suptitle("Synthetic data", y=0.06, x=0.53)
f.tight_layout(rect=[0.05, 0.05, 0.95, 0.95])

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

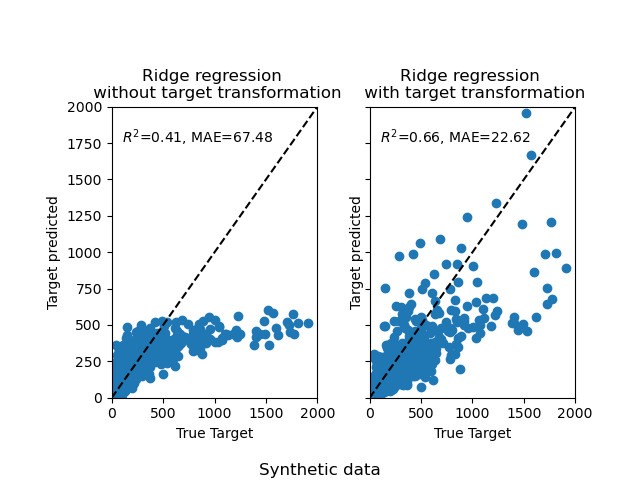
Al principio, se aplicará un modelo lineal a los objetivos originales. Debido a la no linealidad, el modelo entrenado no será preciso durante la predicción. Posteriormente, se utiliza una función logarítmica para linealizar los objetivos, lo que permite una mejor predicción incluso con un modelo lineal similar, como indica la mediana del error absoluto (MAE).

f, (ax0, ax1) = plt.subplots(1, 2, sharey=True)
# Use linear model
regr = RidgeCV()
regr.fit(X_train, y_train)
y_pred = regr.predict(X_test)
# Plot results
ax0.scatter(y_test, y_pred)
ax0.plot([0, 2000], [0, 2000], '--k')
ax0.set_ylabel('Target predicted')
ax0.set_xlabel('True Target')
ax0.set_title('Ridge regression \n without target transformation')
ax0.text(100, 1750, r'$R^2$=%.2f, MAE=%.2f' % (
    r2_score(y_test, y_pred), median_absolute_error(y_test, y_pred)))
ax0.set_xlim([0, 2000])
ax0.set_ylim([0, 2000])
# Transform targets and use same linear model
regr_trans = TransformedTargetRegressor(regressor=RidgeCV(),
                                        func=np.log1p,
                                        inverse_func=np.expm1)
regr_trans.fit(X_train, y_train)
y_pred = regr_trans.predict(X_test)

ax1.scatter(y_test, y_pred)
ax1.plot([0, 2000], [0, 2000], '--k')
ax1.set_ylabel('Target predicted')
ax1.set_xlabel('True Target')
ax1.set_title('Ridge regression \n with target transformation')
ax1.text(100, 1750, r'$R^2$=%.2f, MAE=%.2f' % (
    r2_score(y_test, y_pred), median_absolute_error(y_test, y_pred)))
ax1.set_xlim([0, 2000])
ax1.set_ylim([0, 2000])

f.suptitle("Synthetic data", y=0.035)
f.tight_layout(rect=[0.05, 0.05, 0.95, 0.95])

Conjunto de datos del mundo real

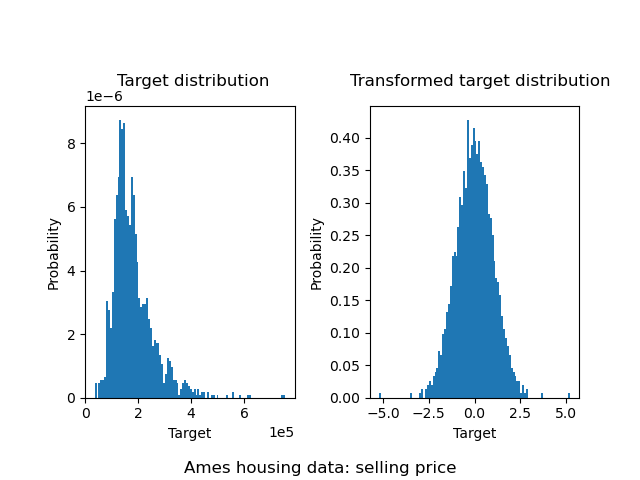
De forma similar, el conjunto de datos de viviendas de Ames se utiliza para mostrar el impacto de la transformación de los objetivos antes de aprender un modelo. En este ejemplo, el objetivo a predecir es el precio de venta de cada vivienda.

from sklearn.datasets import fetch_openml
from sklearn.preprocessing import QuantileTransformer, quantile_transform

ames = fetch_openml(name="house_prices", as_frame=True)
# Keep only numeric columns
X = ames.data.select_dtypes(np.number)
# Remove columns with NaN or Inf values
X = X.drop(columns=['LotFrontage', 'GarageYrBlt', 'MasVnrArea'])
y = ames.target
y_trans = quantile_transform(y.to_frame(),
                             n_quantiles=900,
                             output_distribution='normal',
                             copy=True).squeeze()

Se utiliza un QuantileTransformer para normalizar la distribución objetivo antes de aplicar un modelo RidgeCV.

f, (ax0, ax1) = plt.subplots(1, 2)

ax0.hist(y, bins=100, **density_param)
ax0.set_ylabel('Probability')
ax0.set_xlabel('Target')
ax0.text(s='Target distribution', x=1.2e5, y=9.8e-6, fontsize=12)
ax0.ticklabel_format(axis="both", style="sci", scilimits=(0, 0))

ax1.hist(y_trans, bins=100, **density_param)
ax1.set_ylabel('Probability')
ax1.set_xlabel('Target')
ax1.text(s='Transformed target distribution', x=-6.8, y=0.479, fontsize=12)

f.suptitle("Ames housing data: selling price", y=0.04)
f.tight_layout(rect=[0.05, 0.05, 0.95, 0.95])

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=1)

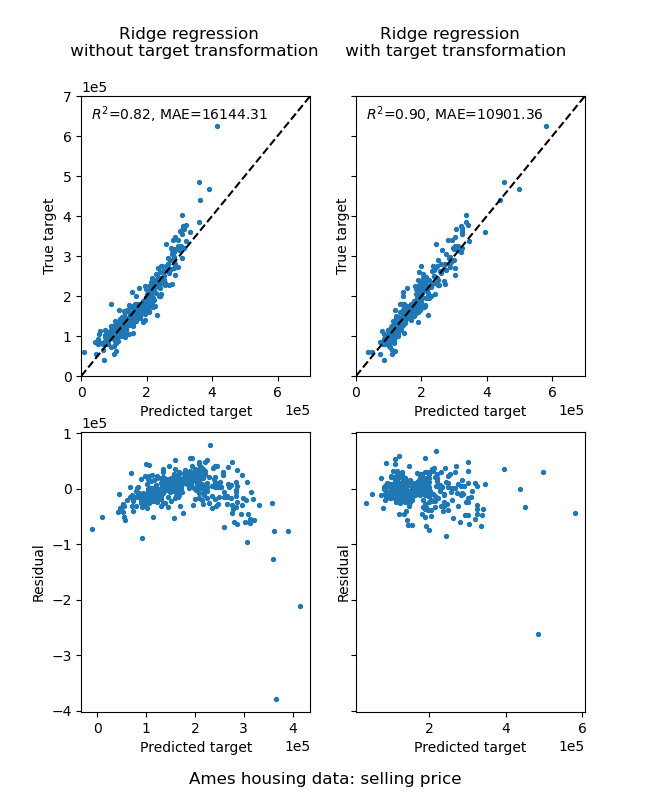
El efecto de la transformación es más débil que en los datos sintéticos. Sin embargo, la transformación produce un aumento de \(R^2\) y una gran disminución del MAE. El gráfico de residuos (objetivo predicho - objetivo verdadero frente a objetivo predicho) sin la transformación del objetivo adquiere una forma curvada, de “reverse smile”, debido a que los valores residuales varían en función del valor del objetivo predicho. Con la transformación del objetivo, la forma es más lineal, lo que indica un mejor ajuste del modelo.

f, (ax0, ax1) = plt.subplots(2, 2, sharey='row', figsize=(6.5, 8))

regr = RidgeCV()
regr.fit(X_train, y_train)
y_pred = regr.predict(X_test)

ax0[0].scatter(y_pred, y_test, s=8)
ax0[0].plot([0, 7e5], [0, 7e5], '--k')
ax0[0].set_ylabel('True target')
ax0[0].set_xlabel('Predicted target')
ax0[0].text(s='Ridge regression \n without target transformation', x=-5e4,
            y=8e5, fontsize=12, multialignment='center')
ax0[0].text(3e4, 64e4, r'$R^2$=%.2f, MAE=%.2f' % (
    r2_score(y_test, y_pred), median_absolute_error(y_test, y_pred)))
ax0[0].set_xlim([0, 7e5])
ax0[0].set_ylim([0, 7e5])
ax0[0].ticklabel_format(axis="both", style="sci", scilimits=(0, 0))

ax1[0].scatter(y_pred, (y_pred - y_test), s=8)
ax1[0].set_ylabel('Residual')
ax1[0].set_xlabel('Predicted target')
ax1[0].ticklabel_format(axis="both", style="sci", scilimits=(0, 0))

regr_trans = TransformedTargetRegressor(
    regressor=RidgeCV(),
    transformer=QuantileTransformer(n_quantiles=900,
                                    output_distribution='normal'))
regr_trans.fit(X_train, y_train)
y_pred = regr_trans.predict(X_test)

ax0[1].scatter(y_pred, y_test, s=8)
ax0[1].plot([0, 7e5], [0, 7e5], '--k')
ax0[1].set_ylabel('True target')
ax0[1].set_xlabel('Predicted target')
ax0[1].text(s='Ridge regression \n with target transformation', x=-5e4,
            y=8e5, fontsize=12, multialignment='center')
ax0[1].text(3e4, 64e4, r'$R^2$=%.2f, MAE=%.2f' % (
    r2_score(y_test, y_pred), median_absolute_error(y_test, y_pred)))
ax0[1].set_xlim([0, 7e5])
ax0[1].set_ylim([0, 7e5])
ax0[1].ticklabel_format(axis="both", style="sci", scilimits=(0, 0))

ax1[1].scatter(y_pred, (y_pred - y_test), s=8)
ax1[1].set_ylabel('Residual')
ax1[1].set_xlabel('Predicted target')
ax1[1].ticklabel_format(axis="both", style="sci", scilimits=(0, 0))

f.suptitle("Ames housing data: selling price", y=0.035)

plt.show()