Comparación de los métodos de Aprendizaje Múltiple

Una ilustración de la reducción de la dimensionalidad en el conjunto de datos de la curva S con varios métodos de aprendizaje múltiple.

Para una discusión y comparación de estos algoritmos, ver la página del módulo manifold

Para un ejemplo similar, donde los métodos se aplican a un conjunto de datos de esfera, ver Métodos de aprendizaje múltiple en una esfera cortada

Ten en cuenta que el propósito del MDS es encontrar una representación de baja dimensión de los datos (aquí 2D) en la que las distancias respeten bien las distancias en el espacio original de alta dimensión, a diferencia de otros algoritmos de aprendizaje múltiple, no busca una representación isotrópica de los datos en el espacio de baja dimensión.

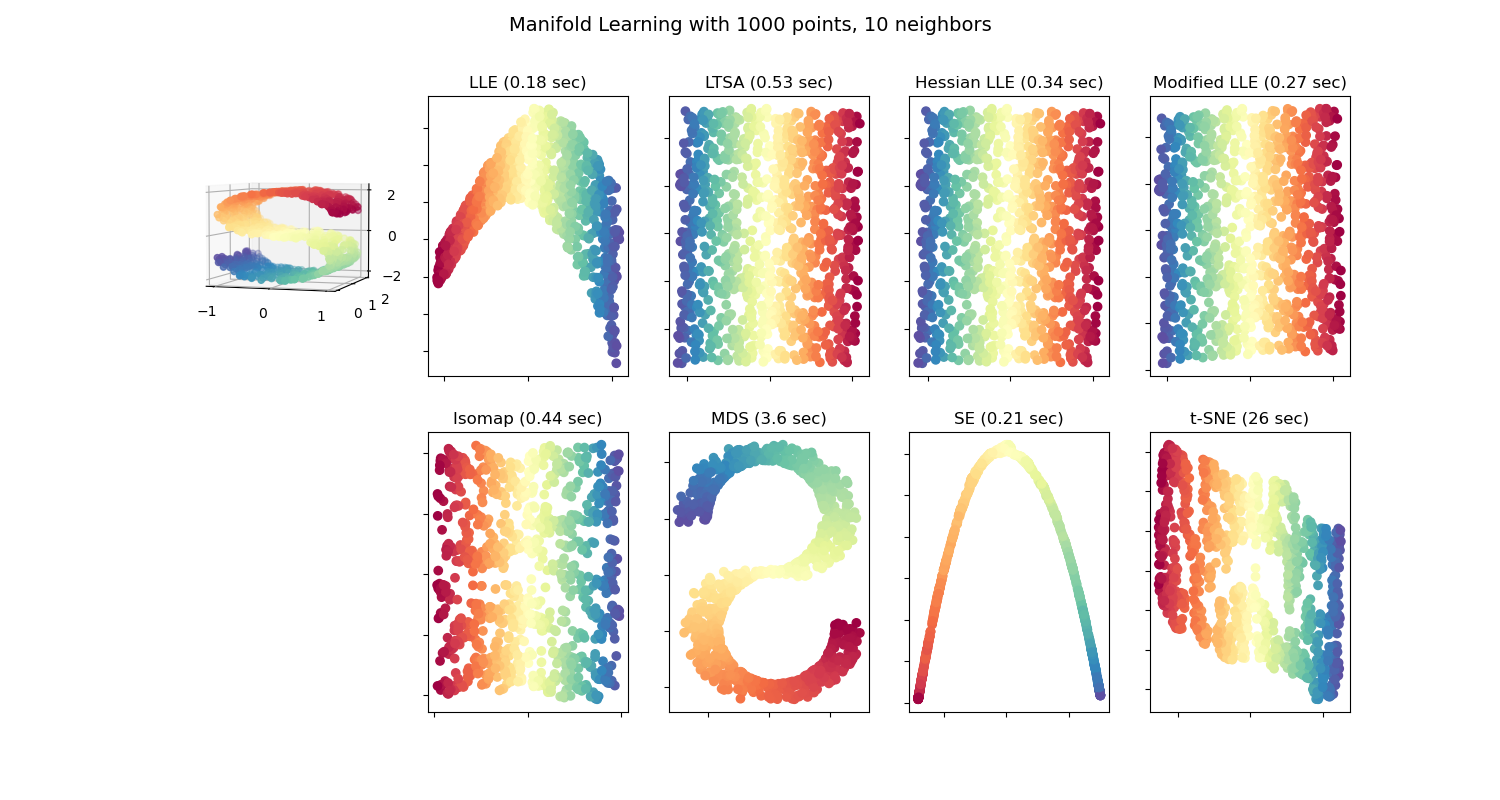
Out:

/home/mapologo/miniconda3/envs/sklearn/lib/python3.9/site-packages/scikit_learn-0.24.1-py3.9-linux-x86_64.egg/sklearn/utils/validation.py:70: FutureWarning: Pass n_neighbors=10, n_components=2 as keyword args. From version 1.0 (renaming of 0.25) passing these as positional arguments will result in an error
  warnings.warn(f"Pass {args_msg} as keyword args. From version "
LLE: 0.18 sec
LTSA: 0.53 sec
Hessian LLE: 0.34 sec
Modified LLE: 0.27 sec
Isomap: 0.44 sec
MDS: 3.6 sec
SE: 0.21 sec
t-SNE: 26 sec

# Author: Jake Vanderplas -- <vanderplas@astro.washington.edu>

print(__doc__)

from collections import OrderedDict
from functools import partial
from time import time

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.ticker import NullFormatter

from sklearn import manifold, datasets

# Next line to silence pyflakes. This import is needed.
Axes3D

n_points = 1000
X, color = datasets.make_s_curve(n_points, random_state=0)
n_neighbors = 10
n_components = 2

# Create figure
fig = plt.figure(figsize=(15, 8))
fig.suptitle("Manifold Learning with %i points, %i neighbors"
             % (1000, n_neighbors), fontsize=14)

# Add 3d scatter plot
ax = fig.add_subplot(251, projection='3d')
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=color, cmap=plt.cm.Spectral)
ax.view_init(4, -72)

# Set-up manifold methods
LLE = partial(manifold.LocallyLinearEmbedding,
              n_neighbors, n_components, eigen_solver='auto')

methods = OrderedDict()
methods['LLE'] = LLE(method='standard')
methods['LTSA'] = LLE(method='ltsa')
methods['Hessian LLE'] = LLE(method='hessian')
methods['Modified LLE'] = LLE(method='modified')
methods['Isomap'] = manifold.Isomap(n_neighbors, n_components)
methods['MDS'] = manifold.MDS(n_components, max_iter=100, n_init=1)
methods['SE'] = manifold.SpectralEmbedding(n_components=n_components,
                                           n_neighbors=n_neighbors)
methods['t-SNE'] = manifold.TSNE(n_components=n_components, init='pca',
                                 random_state=0)

# Plot results
for i, (label, method) in enumerate(methods.items()):
    t0 = time()
    Y = method.fit_transform(X)
    t1 = time()
    print("%s: %.2g sec" % (label, t1 - t0))
    ax = fig.add_subplot(2, 5, 2 + i + (i > 3))
    ax.scatter(Y[:, 0], Y[:, 1], c=color, cmap=plt.cm.Spectral)
    ax.set_title("%s (%.2g sec)" % (label, t1 - t0))
    ax.xaxis.set_major_formatter(NullFormatter())
    ax.yaxis.set_major_formatter(NullFormatter())
    ax.axis('tight')

plt.show()