Métodos de aprendizaje múltiple en una esfera cortada

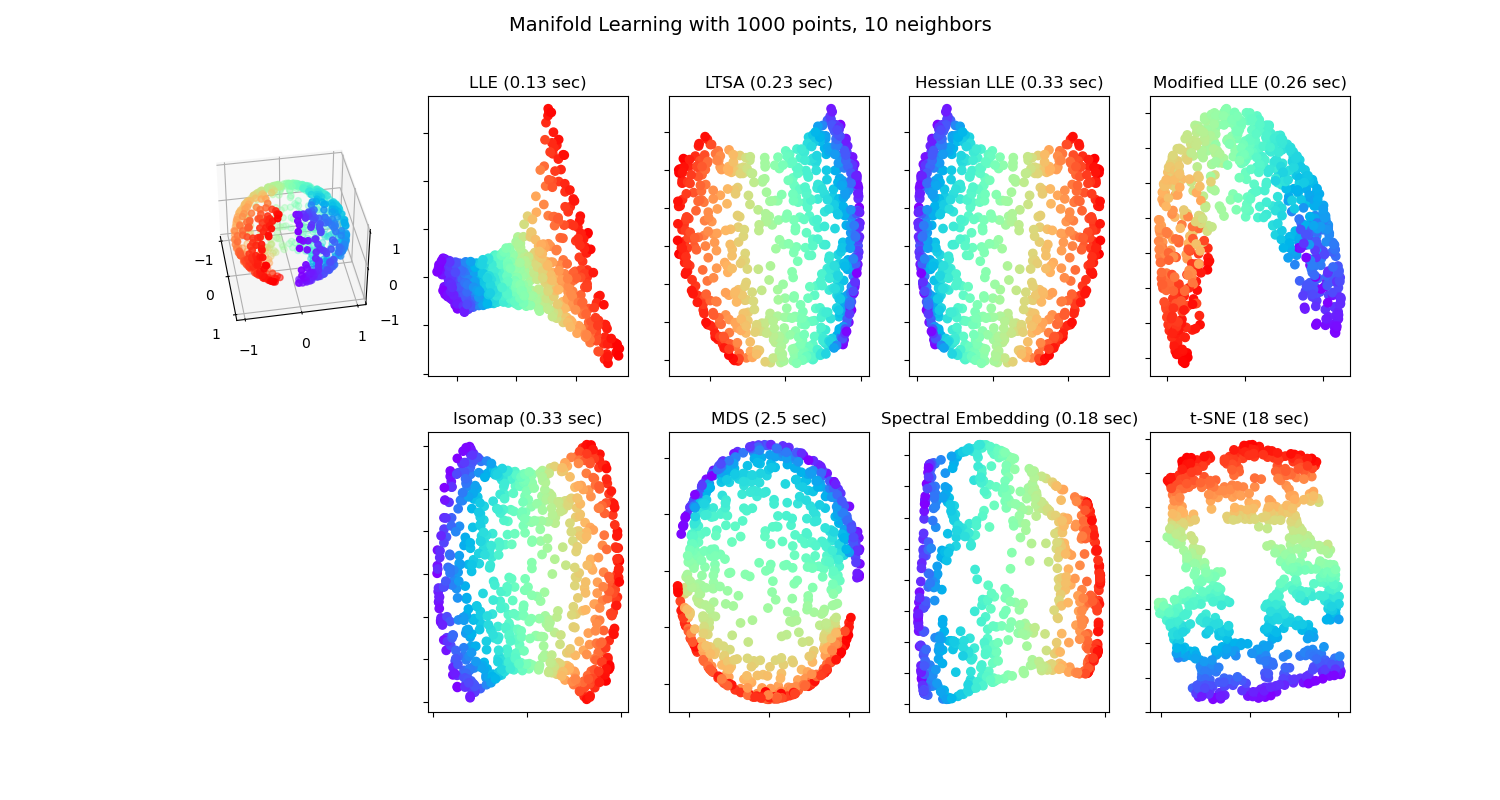
Una aplicación de las diferentes técnicas de Aprendizaje múltiple en un conjunto de datos esféricos. Aquí se puede ver el uso de la reducción de la dimensionalidad con el fin de obtener alguna intuición sobre los métodos de aprendizaje múltiple. En lo que respecta al conjunto de datos, se cortan los polos de la esfera, así como una fina porción de su lado. Esto permite a las técnicas de aprendizaje múltiple «abrirlo» y proyectarlo en dos dimensiones.

Para un ejemplo similar, donde los métodos se aplican a un conjunto de datos de esfera, ver Métodos de aprendizaje múltiple en una esfera cortada

Ten en cuenta que el propósito del MDS es encontrar una representación de baja dimensión de los datos (aquí 2D) en la que las distancias respeten bien las distancias en el espacio original de alta dimensión, a diferencia de otros algoritmos de aprendizaje múltiple, no busca una representación isotrópica de los datos en el espacio de baja dimensión. En este caso, el problema de aprendizaje múltiple coincide bastante con el de la representación de un mapa plano de la Tierra, como con la proyección de mapas

Out:

/home/mapologo/miniconda3/envs/sklearn/lib/python3.9/site-packages/scikit_learn-0.24.1-py3.9-linux-x86_64.egg/sklearn/utils/validation.py:70: FutureWarning: Pass n_neighbors=10, n_components=2 as keyword args. From version 1.0 (renaming of 0.25) passing these as positional arguments will result in an error
  warnings.warn(f"Pass {args_msg} as keyword args. From version "
standard: 0.13 sec
/home/mapologo/miniconda3/envs/sklearn/lib/python3.9/site-packages/scikit_learn-0.24.1-py3.9-linux-x86_64.egg/sklearn/utils/validation.py:70: FutureWarning: Pass n_neighbors=10, n_components=2 as keyword args. From version 1.0 (renaming of 0.25) passing these as positional arguments will result in an error
  warnings.warn(f"Pass {args_msg} as keyword args. From version "
ltsa: 0.23 sec
/home/mapologo/miniconda3/envs/sklearn/lib/python3.9/site-packages/scikit_learn-0.24.1-py3.9-linux-x86_64.egg/sklearn/utils/validation.py:70: FutureWarning: Pass n_neighbors=10, n_components=2 as keyword args. From version 1.0 (renaming of 0.25) passing these as positional arguments will result in an error
  warnings.warn(f"Pass {args_msg} as keyword args. From version "
hessian: 0.33 sec
/home/mapologo/miniconda3/envs/sklearn/lib/python3.9/site-packages/scikit_learn-0.24.1-py3.9-linux-x86_64.egg/sklearn/utils/validation.py:70: FutureWarning: Pass n_neighbors=10, n_components=2 as keyword args. From version 1.0 (renaming of 0.25) passing these as positional arguments will result in an error
  warnings.warn(f"Pass {args_msg} as keyword args. From version "
modified: 0.26 sec
/home/mapologo/miniconda3/envs/sklearn/lib/python3.9/site-packages/scikit_learn-0.24.1-py3.9-linux-x86_64.egg/sklearn/utils/validation.py:70: FutureWarning: Pass n_neighbors=10 as keyword args. From version 1.0 (renaming of 0.25) passing these as positional arguments will result in an error
  warnings.warn(f"Pass {args_msg} as keyword args. From version "
ISO: 0.33 sec
MDS: 2.5 sec
Spectral Embedding: 0.18 sec
t-SNE: 18 sec

# Author: Jaques Grobler <jaques.grobler@inria.fr>
# License: BSD 3 clause

print(__doc__)

from time import time

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.ticker import NullFormatter

from sklearn import manifold
from sklearn.utils import check_random_state

# Next line to silence pyflakes.
Axes3D

# Variables for manifold learning.
n_neighbors = 10
n_samples = 1000

# Create our sphere.
random_state = check_random_state(0)
p = random_state.rand(n_samples) * (2 * np.pi - 0.55)
t = random_state.rand(n_samples) * np.pi

# Sever the poles from the sphere.
indices = ((t < (np.pi - (np.pi / 8))) & (t > ((np.pi / 8))))
colors = p[indices]
x, y, z = np.sin(t[indices]) * np.cos(p[indices]), \
    np.sin(t[indices]) * np.sin(p[indices]), \
    np.cos(t[indices])

# Plot our dataset.
fig = plt.figure(figsize=(15, 8))
plt.suptitle("Manifold Learning with %i points, %i neighbors"
             % (1000, n_neighbors), fontsize=14)

ax = fig.add_subplot(251, projection='3d')
ax.scatter(x, y, z, c=p[indices], cmap=plt.cm.rainbow)
ax.view_init(40, -10)

sphere_data = np.array([x, y, z]).T

# Perform Locally Linear Embedding Manifold learning
methods = ['standard', 'ltsa', 'hessian', 'modified']
labels = ['LLE', 'LTSA', 'Hessian LLE', 'Modified LLE']

for i, method in enumerate(methods):
    t0 = time()
    trans_data = manifold\
        .LocallyLinearEmbedding(n_neighbors, 2,
                                method=method).fit_transform(sphere_data).T
    t1 = time()
    print("%s: %.2g sec" % (methods[i], t1 - t0))

    ax = fig.add_subplot(252 + i)
    plt.scatter(trans_data[0], trans_data[1], c=colors, cmap=plt.cm.rainbow)
    plt.title("%s (%.2g sec)" % (labels[i], t1 - t0))
    ax.xaxis.set_major_formatter(NullFormatter())
    ax.yaxis.set_major_formatter(NullFormatter())
    plt.axis('tight')

# Perform Isomap Manifold learning.
t0 = time()
trans_data = manifold.Isomap(n_neighbors, n_components=2)\
    .fit_transform(sphere_data).T
t1 = time()
print("%s: %.2g sec" % ('ISO', t1 - t0))

ax = fig.add_subplot(257)
plt.scatter(trans_data[0], trans_data[1], c=colors, cmap=plt.cm.rainbow)
plt.title("%s (%.2g sec)" % ('Isomap', t1 - t0))
ax.xaxis.set_major_formatter(NullFormatter())
ax.yaxis.set_major_formatter(NullFormatter())
plt.axis('tight')

# Perform Multi-dimensional scaling.
t0 = time()
mds = manifold.MDS(2, max_iter=100, n_init=1)
trans_data = mds.fit_transform(sphere_data).T
t1 = time()
print("MDS: %.2g sec" % (t1 - t0))

ax = fig.add_subplot(258)
plt.scatter(trans_data[0], trans_data[1], c=colors, cmap=plt.cm.rainbow)
plt.title("MDS (%.2g sec)" % (t1 - t0))
ax.xaxis.set_major_formatter(NullFormatter())
ax.yaxis.set_major_formatter(NullFormatter())
plt.axis('tight')

# Perform Spectral Embedding.
t0 = time()
se = manifold.SpectralEmbedding(n_components=2,
                                n_neighbors=n_neighbors)
trans_data = se.fit_transform(sphere_data).T
t1 = time()
print("Spectral Embedding: %.2g sec" % (t1 - t0))

ax = fig.add_subplot(259)
plt.scatter(trans_data[0], trans_data[1], c=colors, cmap=plt.cm.rainbow)
plt.title("Spectral Embedding (%.2g sec)" % (t1 - t0))
ax.xaxis.set_major_formatter(NullFormatter())
ax.yaxis.set_major_formatter(NullFormatter())
plt.axis('tight')

# Perform t-distributed stochastic neighbor embedding.
t0 = time()
tsne = manifold.TSNE(n_components=2, init='pca', random_state=0)
trans_data = tsne.fit_transform(sphere_data).T
t1 = time()
print("t-SNE: %.2g sec" % (t1 - t0))

ax = fig.add_subplot(2, 5, 10)
plt.scatter(trans_data[0], trans_data[1], c=colors, cmap=plt.cm.rainbow)
plt.title("t-SNE (%.2g sec)" % (t1 - t0))
ax.xaxis.set_major_formatter(NullFormatter())
ax.yaxis.set_major_formatter(NullFormatter())
plt.axis('tight')

plt.show()