Comparación de la cresta del núcleo y la regresión del proceso gaussiano

Tanto la regresión de núcleo ridge (KRR) como la regresión por proceso gaussiano (GPR) aprenden una función objetivo empleando internamente el «truco del núcleo». La KRR aprende una función lineal en el espacio inducido por el núcleo respectivo que corresponde a una función no lineal en el espacio original. La función lineal en el espacio del núcleo se elige en función de la pérdida de error cuadrático medio con regularización de cresta. La GPR utiliza el núcleo para definir la covarianza de una distribución a priori sobre las funciones objetivo y utiliza los datos de entrenamiento observados para definir una función de verosimilitud. Basándose en el teorema de Bayes, se define una distribución posterior (gaussiana) sobre las funciones objetivo, cuya media se utiliza para la predicción.

Una de las principales diferencias es que GPR puede elegir los hiperparámetros del núcleo basándose en el gradiente de ascenso de la función de verosimilitud marginal, mientras que KRR tiene que realizar una búsqueda de cuadrícula en una función de pérdida validada de forma cruzada (pérdida de error cuadrático medio). Otra diferencia es que GPR aprende un modelo generativo y probabilístico de la función objetivo y, por tanto, puede proporcionar intervalos de confianza significativos y muestras posteriores junto con las predicciones, mientras que KRR sólo proporciona predicciones.

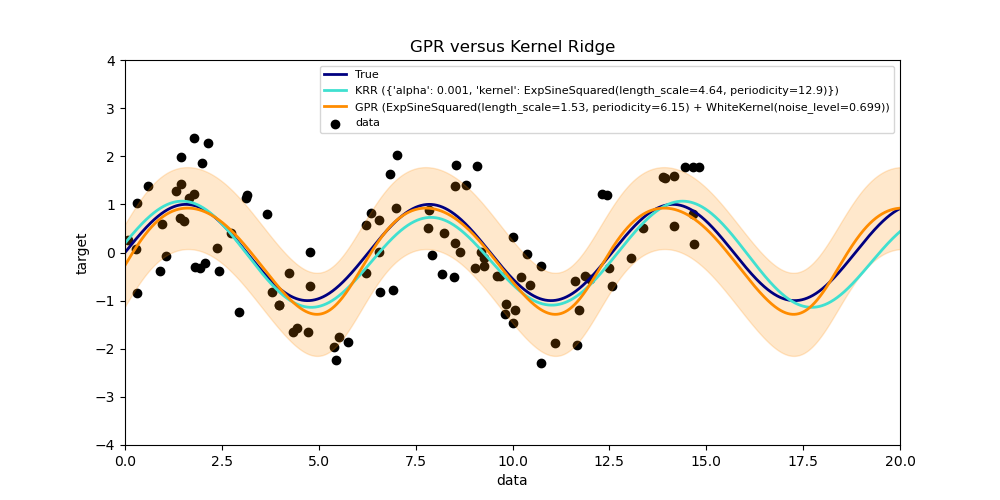
Este ejemplo ilustra ambos métodos en un conjunto de datos artificial, que consiste en una función objetivo sinusoidal y un fuerte ruido. La figura compara el modelo aprendido de KRR y GPR basado en un núcleo ExpSineSquared, que es adecuado para el aprendizaje de funciones periódicas. Los hiperparámetros del núcleo controlan la suavidad (l) y la periodicidad del núcleo (p). Además, el nivel de ruido de los datos es aprendido explícitamente por GPR mediante un componente adicional WhiteKernel en el núcleo y por el parámetro de regularización alfa de KRR.

La figura muestra que ambos métodos aprenden modelos razonables de la función objetivo. GPR identifica correctamente que la periodicidad de la función es aproximadamente 2*pi (6,28), mientras que KRR elige la periodicidad duplicada 4*pi. Además, GPR proporciona límites de confianza razonables en la predicción que no están disponibles para KRR. Una diferencia importante entre los dos métodos es el tiempo necesario para el ajuste y la predicción: mientras que el ajuste de KRR es rápido en principio, la búsqueda en cuadrícula para la optimización de los hiperparámetros escala exponencialmente con el número de hiperparámetros («maldición de la dimensionalidad»). La optimización de los parámetros basada en el gradiente en GPR no sufre este escalamiento exponencial y, por tanto, es considerablemente más rápida en este ejemplo con un espacio de hiperparámetros tridimensional. El tiempo de predicción es similar; sin embargo, generar la varianza de la distribución de predicción de GPR lleva bastante más tiempo que sólo predecir la media.

Out:

Time for KRR fitting: 6.475
Time for GPR fitting: 0.140
Time for KRR prediction: 0.052
Time for GPR prediction: 0.052
Time for GPR prediction with standard-deviation: 0.069

print(__doc__)

# Authors: Jan Hendrik Metzen <jhm@informatik.uni-bremen.de>
# License: BSD 3 clause


import time

import numpy as np

import matplotlib.pyplot as plt

from sklearn.kernel_ridge import KernelRidge
from sklearn.model_selection import GridSearchCV
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import WhiteKernel, ExpSineSquared

rng = np.random.RandomState(0)

# Generate sample data
X = 15 * rng.rand(100, 1)
y = np.sin(X).ravel()
y += 3 * (0.5 - rng.rand(X.shape[0]))  # add noise

# Fit KernelRidge with parameter selection based on 5-fold cross validation
param_grid = {"alpha": [1e0, 1e-1, 1e-2, 1e-3],
              "kernel": [ExpSineSquared(l, p)
                         for l in np.logspace(-2, 2, 10)
                         for p in np.logspace(0, 2, 10)]}
kr = GridSearchCV(KernelRidge(), param_grid=param_grid)
stime = time.time()
kr.fit(X, y)
print("Time for KRR fitting: %.3f" % (time.time() - stime))

gp_kernel = ExpSineSquared(1.0, 5.0, periodicity_bounds=(1e-2, 1e1)) \
    + WhiteKernel(1e-1)
gpr = GaussianProcessRegressor(kernel=gp_kernel)
stime = time.time()
gpr.fit(X, y)
print("Time for GPR fitting: %.3f" % (time.time() - stime))

# Predict using kernel ridge
X_plot = np.linspace(0, 20, 10000)[:, None]
stime = time.time()
y_kr = kr.predict(X_plot)
print("Time for KRR prediction: %.3f" % (time.time() - stime))

# Predict using gaussian process regressor
stime = time.time()
y_gpr = gpr.predict(X_plot, return_std=False)
print("Time for GPR prediction: %.3f" % (time.time() - stime))

stime = time.time()
y_gpr, y_std = gpr.predict(X_plot, return_std=True)
print("Time for GPR prediction with standard-deviation: %.3f"
      % (time.time() - stime))

# Plot results
plt.figure(figsize=(10, 5))
lw = 2
plt.scatter(X, y, c='k', label='data')
plt.plot(X_plot, np.sin(X_plot), color='navy', lw=lw, label='True')
plt.plot(X_plot, y_kr, color='turquoise', lw=lw,
         label='KRR (%s)' % kr.best_params_)
plt.plot(X_plot, y_gpr, color='darkorange', lw=lw,
         label='GPR (%s)' % gpr.kernel_)
plt.fill_between(X_plot[:, 0], y_gpr - y_std, y_gpr + y_std, color='darkorange',
                 alpha=0.2)
plt.xlabel('data')
plt.ylabel('target')
plt.xlim(0, 20)
plt.ylim(-4, 4)
plt.title('GPR versus Kernel Ridge')
plt.legend(loc="best",  scatterpoints=1, prop={'size': 8})
plt.show()