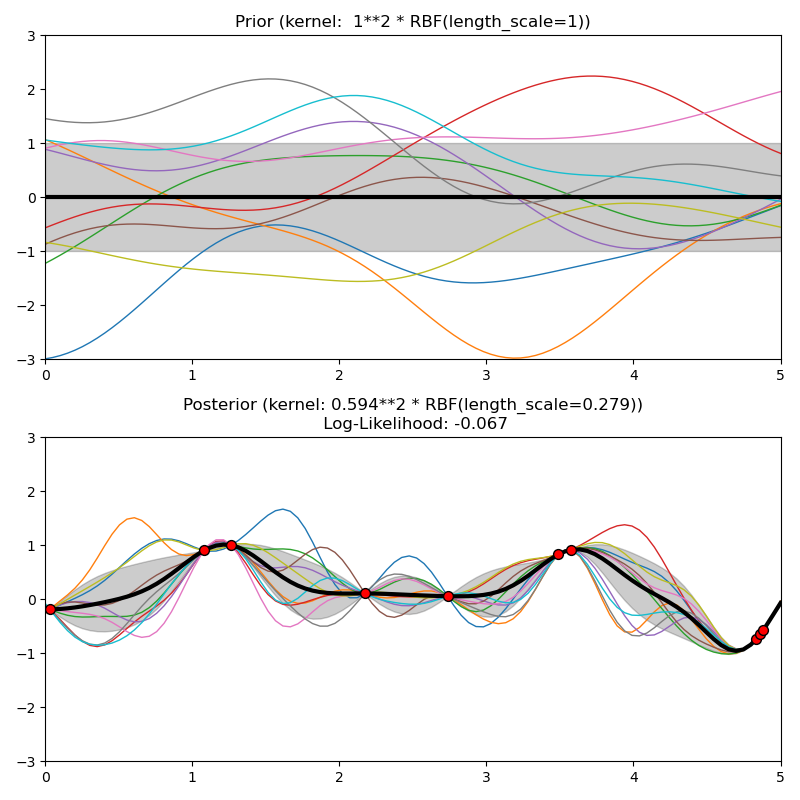
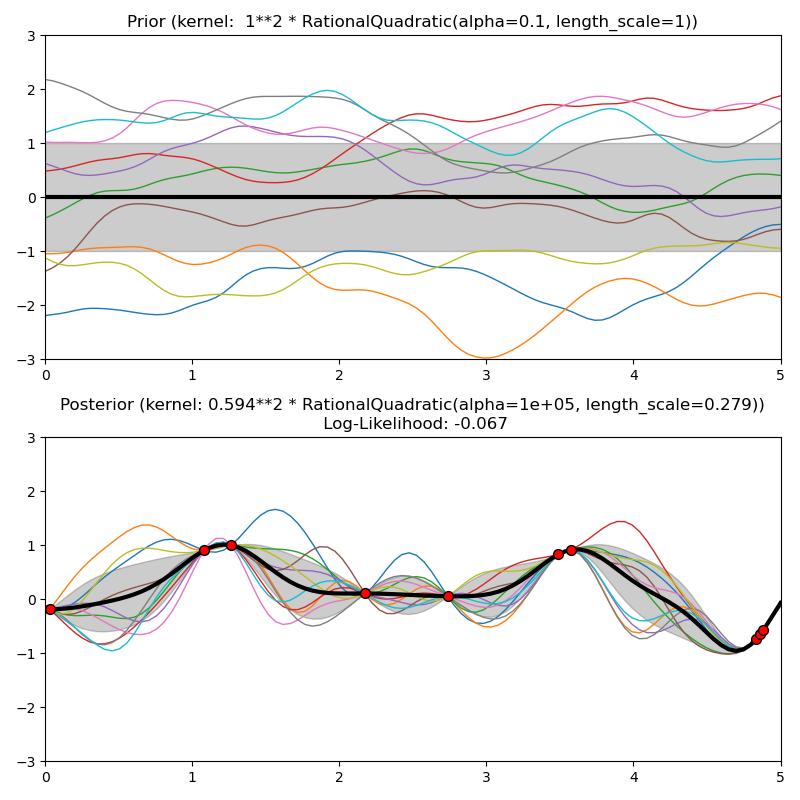
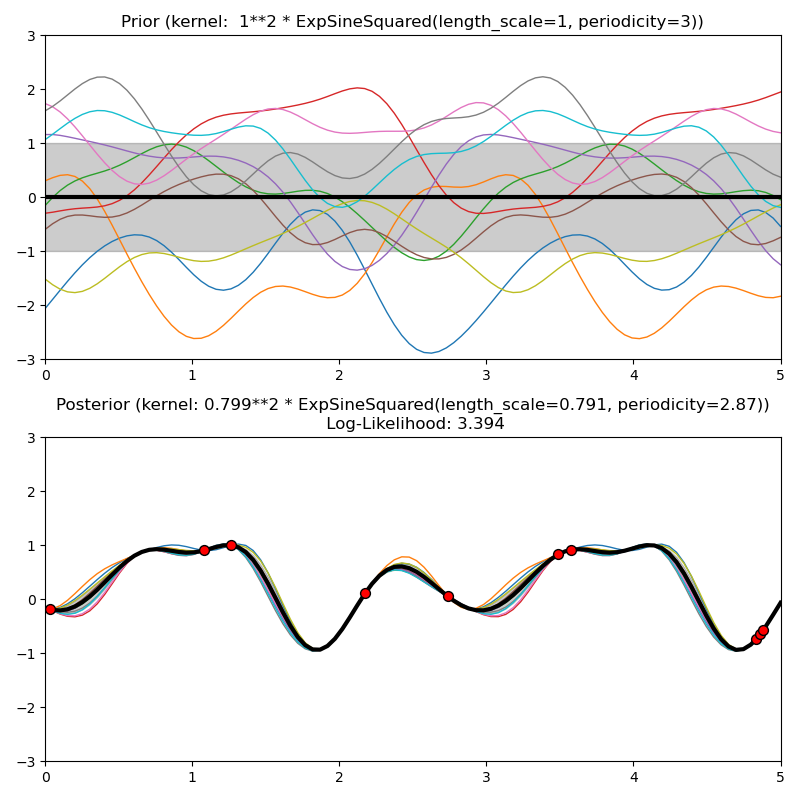
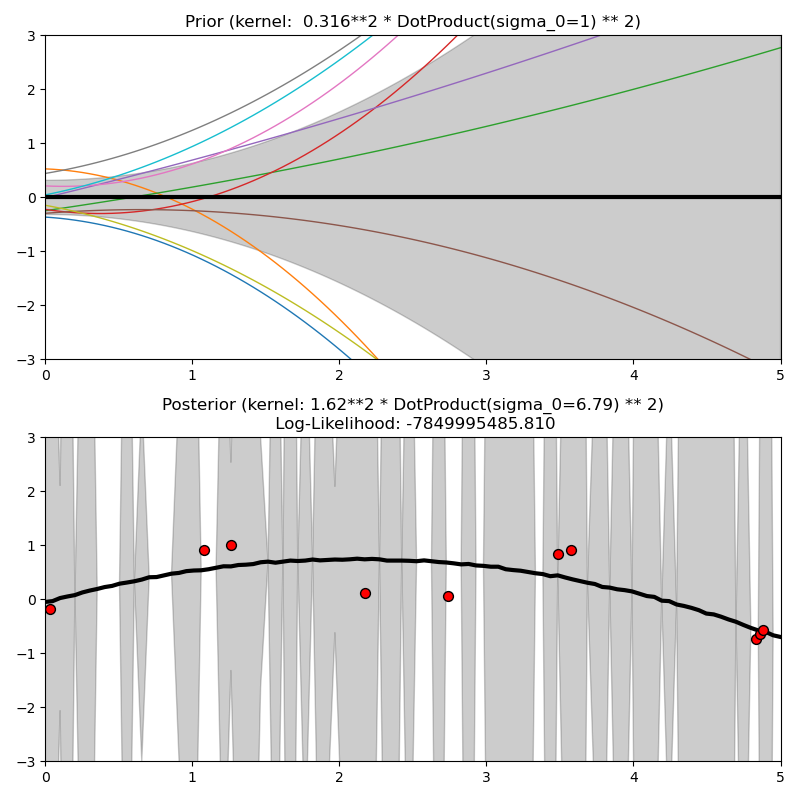
Illustración del proceso Gaussiano anterior y posterior para diferentes núcleos

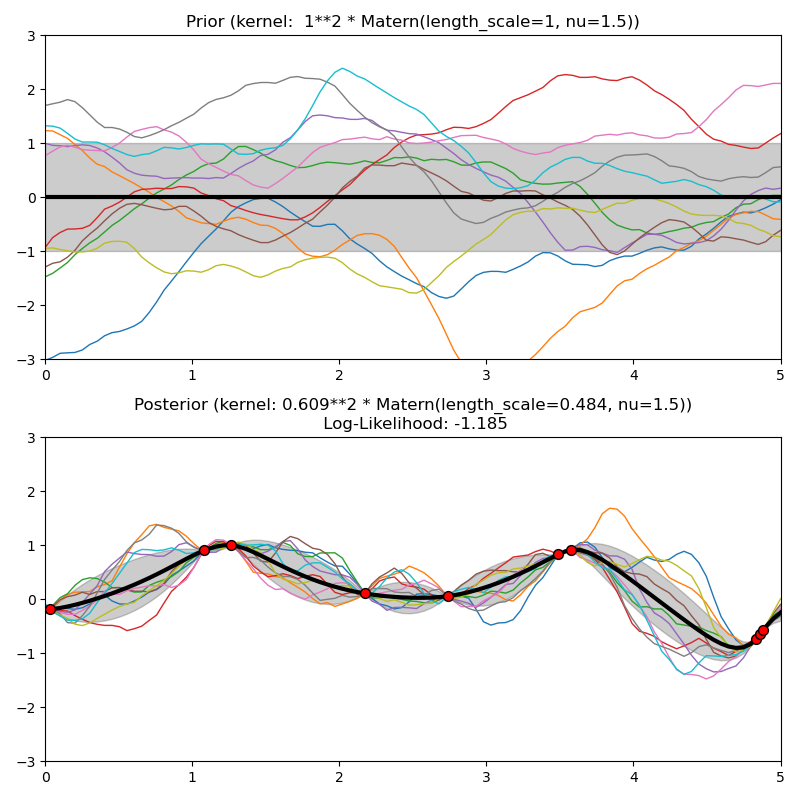
Este ejemplo ilustra el anterior y posterior de un GPR con diferentes núcleos. Se muestran muestras de significado, desviación estándar y 10 muestras tanto para antes como para después.

• 
• 
• 
• 
• 

Out:

/home/mapologo/miniconda3/envs/sklearn/lib/python3.9/site-packages/scikit_learn-0.24.1-py3.9-linux-x86_64.egg/sklearn/gaussian_process/kernels.py:411: ConvergenceWarning: The optimal value found for dimension 0 of parameter k2__alpha is close to the specified upper bound 100000.0. Increasing the bound and calling fit again may find a better value.
  warnings.warn("The optimal value found for "
/home/mapologo/miniconda3/envs/sklearn/lib/python3.9/site-packages/scikit_learn-0.24.1-py3.9-linux-x86_64.egg/sklearn/gaussian_process/_gpr.py:375: UserWarning: Predicted variances smaller than 0. Setting those variances to 0.
  warnings.warn("Predicted variances smaller than 0. "

print(__doc__)

# Authors: Jan Hendrik Metzen <jhm@informatik.uni-bremen.de>
#
# License: BSD 3 clause

import numpy as np

from matplotlib import pyplot as plt

from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import (RBF, Matern, RationalQuadratic,
                                              ExpSineSquared, DotProduct,
                                              ConstantKernel)


kernels = [1.0 * RBF(length_scale=1.0, length_scale_bounds=(1e-1, 10.0)),
           1.0 * RationalQuadratic(length_scale=1.0, alpha=0.1),
           1.0 * ExpSineSquared(length_scale=1.0, periodicity=3.0,
                                length_scale_bounds=(0.1, 10.0),
                                periodicity_bounds=(1.0, 10.0)),
           ConstantKernel(0.1, (0.01, 10.0))
               * (DotProduct(sigma_0=1.0, sigma_0_bounds=(0.1, 10.0)) ** 2),
           1.0 * Matern(length_scale=1.0, length_scale_bounds=(1e-1, 10.0),
                        nu=1.5)]

for kernel in kernels:
    # Specify Gaussian Process
    gp = GaussianProcessRegressor(kernel=kernel)

    # Plot prior
    plt.figure(figsize=(8, 8))
    plt.subplot(2, 1, 1)
    X_ = np.linspace(0, 5, 100)
    y_mean, y_std = gp.predict(X_[:, np.newaxis], return_std=True)
    plt.plot(X_, y_mean, 'k', lw=3, zorder=9)
    plt.fill_between(X_, y_mean - y_std, y_mean + y_std,
                     alpha=0.2, color='k')
    y_samples = gp.sample_y(X_[:, np.newaxis], 10)
    plt.plot(X_, y_samples, lw=1)
    plt.xlim(0, 5)
    plt.ylim(-3, 3)
    plt.title("Prior (kernel:  %s)" % kernel, fontsize=12)

    # Generate data and fit GP
    rng = np.random.RandomState(4)
    X = rng.uniform(0, 5, 10)[:, np.newaxis]
    y = np.sin((X[:, 0] - 2.5) ** 2)
    gp.fit(X, y)

    # Plot posterior
    plt.subplot(2, 1, 2)
    X_ = np.linspace(0, 5, 100)
    y_mean, y_std = gp.predict(X_[:, np.newaxis], return_std=True)
    plt.plot(X_, y_mean, 'k', lw=3, zorder=9)
    plt.fill_between(X_, y_mean - y_std, y_mean + y_std,
                     alpha=0.2, color='k')

    y_samples = gp.sample_y(X_[:, np.newaxis], 10)
    plt.plot(X_, y_samples, lw=1)
    plt.scatter(X[:, 0], y, c='r', s=50, zorder=10, edgecolors=(0, 0, 0))
    plt.xlim(0, 5)
    plt.ylim(-3, 3)
    plt.title("Posterior (kernel: %s)\n Log-Likelihood: %.3f"
              % (gp.kernel_, gp.log_marginal_likelihood(gp.kernel_.theta)),
              fontsize=12)
    plt.tight_layout()

plt.show()