`sklearn.gaussian_process.kernels`.DotProduct¶

class sklearn.gaussian_process.kernels.DotProduct¶

Núcleo de producto punto.

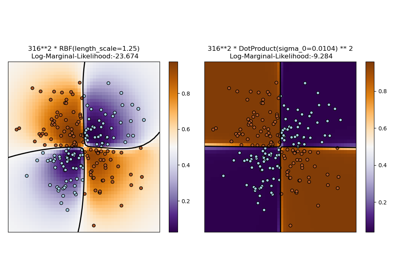
El núcleo DotProduct no es estacionario y se puede obtener a partir de la regresión lineal poniendo \(N(0, 1)\) priores en los coeficientes de \(x_d (d = 1, . . , D)\) y un prior de \(N(0, \sigma_0^2)\) en el sesgo. El núcleo DotProduct es invariante a una rotación de las coordenadas sobre el origen, pero no a las traslaciones. Está parametrizado por un parámetro sigma_0 \(\sigma\) que controla la inhomogeneidad del núcleo. Para \(\sigma_0^2 =0\), el núcleo se denomina núcleo lineal homogéneo, en caso contrario es inhomogéneo. El núcleo viene dado por

\[k(x_i, x_j) = \sigma_0 ^ 2 + x_i \cdot x_j\]

El núcleo DotProduct se suele combinar con la exponenciación.

Consulta [1], Capítulo 4, Sección 4.2, para más detalles sobre el núcleo DotProduct.

Más información en la Manual de usuario.

Nuevo en la versión 0.18.

Parámetros

sigma_0float >= 0, default=1.0: Parámetro que controla la inhomogeneidad del núcleo. Si sigma_0=0, el núcleo es homogéneo.
sigma_0_boundspar de flotantes >= 0 or «fixed», default=(1e-5, 1e5): El límite inferior y superior de “sigma_0”. Si se establece como «fixed», “sigma_0” no puede cambiarse durante el ajuste de los hiperparámetros.

Atributos

bounds: Devuelve los límites transformados en logaritmo del theta.
hyperparameter_sigma_0
hyperparameters: Devuelve una lista de todas las especificaciones de los hiperparámetros.
n_dims: Devuelve el número de hiperparámetros no fijos del núcleo.
requires_vector_input: Devuelve si el núcleo está definido en vectores de características de longitud fija o en objetos genéricos.
theta: Devuelve los hiperparámetros no fijos (aplanados y transformados en logaritmos).

Referencias

1: Carl Edward Rasmussen, Christopher K. I. Williams (2006). «Gaussian Processes for Machine Learning». The MIT Press.

Ejemplos

>>> from sklearn.datasets import make_friedman2
>>> from sklearn.gaussian_process import GaussianProcessRegressor
>>> from sklearn.gaussian_process.kernels import DotProduct, WhiteKernel
>>> X, y = make_friedman2(n_samples=500, noise=0, random_state=0)
>>> kernel = DotProduct() + WhiteKernel()
>>> gpr = GaussianProcessRegressor(kernel=kernel,
...         random_state=0).fit(X, y)
>>> gpr.score(X, y)
0.3680...
>>> gpr.predict(X[:2,:], return_std=True)
(array([653.0..., 592.1...]), array([316.6..., 316.6...]))

Métodos

`__call__`	Devuelve el núcleo k(X, Y) y opcionalmente su gradiente.
`clone_with_theta`	Devuelve un clon de sí mismo con los hiperparámetros dados theta.
`diag`	Devuelve la diagonal del núcleo k(X, X).
`get_params`	Establece los parámetros de este núcleo.
`is_stationary`	Devuelve si el núcleo es estacionario.
`set_params`	Establece los parámetros de este núcleo.

__call__()¶

Devuelve el núcleo k(X, Y) y opcionalmente su gradiente.

Parámetros

Xndarray de forma (n_samples_X, n_features): Argumento izquierdo del núcleo devuelto k(X, Y)
Yndarray de forma (n_samples_Y, n_features), default=None: Argumento derecho del núcleo devuelto k(X, Y). Si es None, se evalúa k(X, X) en su lugar.
eval_gradientbool, default=False: Determina si se calcula el gradiente con respecto al logaritmo del hiperparámetro del núcleo. Sólo se admite cuando Y es None.

Devuelve

Kndarray de forma (n_samples_X, n_samples_Y): Núcleo k(X, Y)
K_gradientndarray de forma (n_samples_X, n_samples_X, n_dims), opcional: El gradiente del núcleo k(X, X) con respecto al logaritmo del hiperparámetro del núcleo. Sólo se devuelve cuando eval_gradient es True.

property bounds¶

Devuelve los límites transformados en logaritmo del theta.

Devuelve

boundsndarray de forma (n_dims, 2): Los límites transformados logarítmicamente de los hiperparámetros del núcleo theta

clone_with_theta()¶

Devuelve un clon de sí mismo con los hiperparámetros dados theta.

Parámetros

thetandarray de forma (n_dims,): Hiperparámetros

diag()¶

Devuelve la diagonal del núcleo k(X, X).

El resultado de este método es idéntico al de np.diag(self(X)); sin embargo, se puede evaluar de forma más eficiente ya que sólo se evalúa la diagonal.

Parámetros

Xndarray de forma (n_samples_X, n_features): Argumento izquierdo del núcleo devuelto k(X, Y).

Devuelve

K_diagndarray de forma (n_samples_X,): Diagonal del núcleo k(X, X).

get_params()¶

Establece los parámetros de este núcleo.

Parámetros

deepbool, default=True: Si es True, devolverá los parámetros para este estimador y los subobjetos contenidos que son estimadores.

Devuelve

parámetrosdict: Nombres de parámetros mapeados a sus valores.

property hyperparameters¶: Devuelve una lista de todas las especificaciones de los hiperparámetros.

is_stationary()¶: Devuelve si el núcleo es estacionario.

property n_dims¶: Devuelve el número de hiperparámetros no fijos del núcleo.

property requires_vector_input¶: Devuelve si el núcleo está definido en vectores de características de longitud fija o en objetos genéricos. El valor predeterminado es True para la compatibilidad con versiones anteriores.

set_params()¶

Establece los parámetros de este núcleo.

El método funciona tanto en núcleos simples como en núcleos anidados. Estos últimos tienen parámetros de la forma <component>__<parameter> para que sea posible actualizar cada componente de un objeto anidado.

Devuelve

self

property theta¶

Devuelve los hiperparámetros no fijos (aplanados y transformados en logaritmos).

Ten en cuenta que theta son típicamente los valores transformados en logaritmos de los hiperparámetros del núcleo, ya que esta representación del espacio de búsqueda es más adecuada para la búsqueda de hiperparámetros, ya que los hiperparámetros como las escalas de longitud viven naturalmente en una escala logarítmica.

Devuelve

thetandarray de forma (n_dims,): Los hiperparámetros no fijos y transformados en logaritmos del núcleo

Ejemplos usando `sklearn.gaussian_process.kernels.DotProduct`¶

sklearn.gaussian_process.kernels.DotProduct¶

Ejemplos usando sklearn.gaussian_process.kernels.DotProduct¶

`sklearn.gaussian_process.kernels`.DotProduct¶

Ejemplos usando `sklearn.gaussian_process.kernels.DotProduct`¶