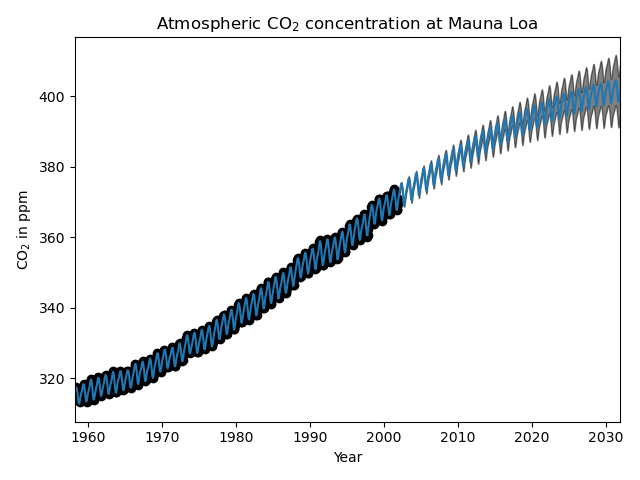
Regresión del proceso gaussiano (GPR) en los datos de CO2 de Mauna Loa.

Este ejemplo se basa en la Sección 5.4.3 de «Gaussian Processes for Machine Learning» [RW2006]. Ilustra un ejemplo de ingeniería de kernel complejo y optimización de hiperparámetros utilizando el ascenso de gradiente en el logaritmo de la verosimilitud marginal. Los datos consisten en las concentraciones promedios mensuales de CO2 atmosférico (en partes por millón en volumen (ppmv)) recogidas en el Observatorio de Mauna Loa en Hawai, entre 1958 y 2001. El objetivo es modelar la concentración de CO2 en función del tiempo t.

El núcleo se compone de varios términos que son responsables de explicar diferentes propiedades de la señal:

• una tendencia suave y ascendente a largo plazo debe ser explicada por un núcleo RBF. El núcleo RBF con una gran escala de longitud obliga a que este componente sea suave; no se obliga a que la tendencia sea ascendente, lo que deja esta elección a la GP. La escala de longitud específica y la amplitud son hiperparámetros libres.

• un componente estacional, que debe ser explicado por el núcleo periódico ExpSineSquared con una periodicidad fija de 1 año. La escala de longitud de este componente periódico, que controla su suavidad, es un parámetro libre. Para permitir el decaimiento de la periodicidad exacta, se toma el producto con un núcleo RBF. La escala de longitud de este componente RBF controla el tiempo de decaimiento y es otro parámetro libre.

• las irregularidades más pequeñas y a medio plazo deben explicarse mediante un componente núcleo RationalQuadratic, cuya escala de longitud y parámetro alfa, que determina la difusividad de las escalas de longitud, deben determinarse. Según [RW2006], estas irregularidades se pueden explicar mejor con un componente núcleo RationalQuadratic que con uno RBF, probablemente porque puede acomodar varias escalas de longitud.

• un término de «ruido», que consiste en una contribución del núcleo RBF, que explicará los componentes de ruido correlacionados, como los fenómenos meteorológicos locales, y una contribución del WhiteKernel para el ruido blanco. Las amplitudes relativas y la escala de longitud del RBF son otros parámetros libres.

Al maximizar la verosimilitud marginal logarítmica después de restar la media del objetivo, se obtiene el siguiente núcleo con un LML de -83,214:

34.4**2 * RBF(length_scale=41.8)
+ 3.27**2 * RBF(length_scale=180) * ExpSineSquared(length_scale=1.44,
                                                   periodicity=1)
+ 0.446**2 * RationalQuadratic(alpha=17.7, length_scale=0.957)
+ 0.197**2 * RBF(length_scale=0.138) + WhiteKernel(noise_level=0.0336)

Así, la mayor parte de la señal objetivo (34,4ppm) se explica por una tendencia ascendente a largo plazo (escala de longitud de 41,8 años). El componente periódico tiene una amplitud de 3,27 ppm, un tiempo de decaimiento de 180 años y una escala de longitud de 1,44. El largo tiempo de decaimiento indica que tenemos una componente estacional localmente muy cercana a la periódica. El ruido correlacionado tiene una amplitud de 0,197ppm con una escala de longitud de 0,138 años y una contribución de ruido blanco de 0,197ppm. Por tanto, el nivel de ruido global es muy pequeño, lo que indica que los datos pueden ser explicados muy bien por el modelo. La figura muestra también que el modelo realiza predicciones muy seguras hasta aproximadamente 2015.

Out:

GPML kernel: 66**2 * RBF(length_scale=67) + 2.4**2 * RBF(length_scale=90) * ExpSineSquared(length_scale=1.3, periodicity=1) + 0.66**2 * RationalQuadratic(alpha=0.78, length_scale=1.2) + 0.18**2 * RBF(length_scale=0.134) + WhiteKernel(noise_level=0.0361)
Log-marginal-likelihood: 155.006

Learned kernel: 2.63**2 * RBF(length_scale=51.6) + 0.155**2 * RBF(length_scale=91.5) * ExpSineSquared(length_scale=1.48, periodicity=1) + 0.0314**2 * RationalQuadratic(alpha=2.89, length_scale=0.968) + 0.011**2 * RBF(length_scale=0.122) + WhiteKernel(noise_level=0.000126)
Log-marginal-likelihood: 1362.655

# Authors: Jan Hendrik Metzen <jhm@informatik.uni-bremen.de>
#
# License: BSD 3 clause


import numpy as np

from matplotlib import pyplot as plt
from sklearn.datasets import fetch_openml
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels \
    import RBF, WhiteKernel, RationalQuadratic, ExpSineSquared

print(__doc__)


def load_mauna_loa_atmospheric_co2():
    ml_data = fetch_openml(data_id=41187, as_frame=False)
    months = []
    ppmv_sums = []
    counts = []

    y = ml_data.data[:, 0]
    m = ml_data.data[:, 1]
    month_float = y + (m - 1) / 12
    ppmvs = ml_data.target

    for month, ppmv in zip(month_float, ppmvs):
        if not months or month != months[-1]:
            months.append(month)
            ppmv_sums.append(ppmv)
            counts.append(1)
        else:
            # aggregate monthly sum to produce average
            ppmv_sums[-1] += ppmv
            counts[-1] += 1

    months = np.asarray(months).reshape(-1, 1)
    avg_ppmvs = np.asarray(ppmv_sums) / counts
    return months, avg_ppmvs


X, y = load_mauna_loa_atmospheric_co2()

# Kernel with parameters given in GPML book
k1 = 66.0**2 * RBF(length_scale=67.0)  # long term smooth rising trend
k2 = 2.4**2 * RBF(length_scale=90.0) \
    * ExpSineSquared(length_scale=1.3, periodicity=1.0)  # seasonal component
# medium term irregularity
k3 = 0.66**2 \
    * RationalQuadratic(length_scale=1.2, alpha=0.78)
k4 = 0.18**2 * RBF(length_scale=0.134) \
    + WhiteKernel(noise_level=0.19**2)  # noise terms
kernel_gpml = k1 + k2 + k3 + k4

gp = GaussianProcessRegressor(kernel=kernel_gpml, alpha=0,
                              optimizer=None, normalize_y=True)
gp.fit(X, y)

print("GPML kernel: %s" % gp.kernel_)
print("Log-marginal-likelihood: %.3f"
      % gp.log_marginal_likelihood(gp.kernel_.theta))

# Kernel with optimized parameters
k1 = 50.0**2 * RBF(length_scale=50.0)  # long term smooth rising trend
k2 = 2.0**2 * RBF(length_scale=100.0) \
    * ExpSineSquared(length_scale=1.0, periodicity=1.0,
                     periodicity_bounds="fixed")  # seasonal component
# medium term irregularities
k3 = 0.5**2 * RationalQuadratic(length_scale=1.0, alpha=1.0)
k4 = 0.1**2 * RBF(length_scale=0.1) \
    + WhiteKernel(noise_level=0.1**2,
                  noise_level_bounds=(1e-5, np.inf))  # noise terms
kernel = k1 + k2 + k3 + k4

gp = GaussianProcessRegressor(kernel=kernel, alpha=0,
                              normalize_y=True)
gp.fit(X, y)

print("\nLearned kernel: %s" % gp.kernel_)
print("Log-marginal-likelihood: %.3f"
      % gp.log_marginal_likelihood(gp.kernel_.theta))

X_ = np.linspace(X.min(), X.max() + 30, 1000)[:, np.newaxis]
y_pred, y_std = gp.predict(X_, return_std=True)

# Illustration
plt.scatter(X, y, c='k')
plt.plot(X_, y_pred)
plt.fill_between(X_[:, 0], y_pred - y_std, y_pred + y_std,
                 alpha=0.5, color='k')
plt.xlim(X_.min(), X_.max())
plt.xlabel("Year")
plt.ylabel(r"CO$_2$ in ppm")
plt.title(r"Atmospheric CO$_2$ concentration at Mauna Loa")
plt.tight_layout()
plt.show()